
Prismatic uniform polyhedron
Encyclopedia

Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, a prismatic uniform polyhedron is a uniform polyhedron
Uniform polyhedron
A uniform polyhedron is a polyhedron which has regular polygons as faces and is vertex-transitive...
with dihedral symmetry
Dihedral symmetry in three dimensions
This article deals with three infinite sequences of point groups in three dimensions which have a symmetry group that as abstract group is a dihedral group Dihn .See also point groups in two dimensions.Chiral:...
. They exist in two infinite families, the uniform prisms
Prism (geometry)
In geometry, a prism is a polyhedron with an n-sided polygonal base, a translated copy , and n other faces joining corresponding sides of the two bases. All cross-sections parallel to the base faces are the same. Prisms are named for their base, so a prism with a pentagonal base is called a...
and the uniform antiprism
Antiprism
In geometry, an n-sided antiprism is a polyhedron composed of two parallel copies of some particular n-sided polygon, connected by an alternating band of triangles...
s. All have their vertices in parallel planes and are therefore prismatoid
Prismatoid
In geometry, a prismatoid is a polyhedron where all vertices lie in two parallel planes....
s.
Vertex configuration and symmetry groups
Because they are isogonalIsogonal
Isogonal is a mathematical term which means "having similar angles". It occurs in several contexts:*Isogonal polygon, polyhedron, polytope or tiling.*Isogonal trajectory in curve theory.*Isogonal conjugate in triangle geometry....
(vertex-transitive), their vertex arrangement
Vertex arrangement
In geometry, a vertex arrangement is a set of points in space described by their relative positions. They can be described by their use in polytopes....
uniquely corresponds to a symmetry group
Point groups in three dimensions
In geometry, a point group in three dimensions is an isometry group in three dimensions that leaves the origin fixed, or correspondingly, an isometry group of a sphere. It is a subgroup of the orthogonal group O, the group of all isometries that leave the origin fixed, or correspondingly, the group...
.
The difference between the prismatic and antiprismatic symmetry groups is that Dph has the vertices lined up in both planes, which gives it a reflection plane perpendicular to its p-fold axis (parallel to the {p/q} polygon); while Dpd has the vertices twisted relative to the other plane, which gives it a rotatory reflection. Each has p reflection planes which contain the p-fold axis.
The Dph symmetry group contains inversion if and only if p is even, while Dpd contains inversion symmetry if and only if p is odd.
Enumeration
There are:- prismPrism (geometry)In geometry, a prism is a polyhedron with an n-sided polygonal base, a translated copy , and n other faces joining corresponding sides of the two bases. All cross-sections parallel to the base faces are the same. Prisms are named for their base, so a prism with a pentagonal base is called a...
s, for each rational number p/q > 2, with symmetry group Dph; - antiprismAntiprismIn geometry, an n-sided antiprism is a polyhedron composed of two parallel copies of some particular n-sided polygon, connected by an alternating band of triangles...
s, for each rational number p/q > 3/2, with symmetry group Dpd if q is odd, Dph if q is even.
If p/q is an integer, i.e. if q = 1, the prism or antiprism is convex. (The fraction is always assumed to be stated in lowest terms.)
An antiprism with p/q < 2 is crossed or retrograde; its vertex figure
Vertex figure
In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:...
resembles a bowtie. If p/q ≤ 3/2 no uniform antiprism can exist, as its vertex figure would have to violate the triangle inequality
Triangle inequality
In mathematics, the triangle inequality states that for any triangle, the sum of the lengths of any two sides must be greater than or equal to the length of the remaining side ....
.
Images
Note: The cubeCube
In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and...
and octahedron
Octahedron
In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....
are listed here with dihedral symmetry (as a square prism and triangular antiprism respectively), although if uniformly colored, they also have octahedral symmetry.
| Symmetry group | Convex | Star forms | ||||||
|---|---|---|---|---|---|---|---|---|
| d3h, [2,3], (*223) |  3.4.4 Triangular prism In geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides.... |
|||||||
| d3d, [2+,3], (2*3) |  3.3.3.3 Octahedron In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex.... |
|||||||
| d4h, [2,4], (*224) | 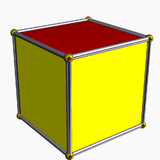 4.4.4 Cube In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and... |
|||||||
| d4d, [2+,4], (2*4) | 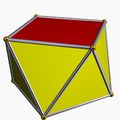 3.3.3.4 Square antiprism In geometry, the square antiprism is the second in an infinite set of antiprisms formed by an even-numbered sequence of triangle sides closed by two polygon caps... |
|||||||
| d5h, [2,5], (*225) |  4.4.5 Pentagonal prism In geometry, the pentagonal prism is a prism with a pentagonal base. It is a type of heptahedron with 7 faces, 15 edges, and 10 vertices.- As a semiregular polyhedron :... |
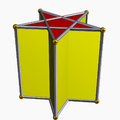 4.4.5/2 Pentagrammic prism In geometry, the pentagrammic prism is one in an infinite set of nonconvex prisms formed by square sides and two regular star polygon caps, in this case two pentagrams.This polyhedron is identified with the indexed name U78 as a uniform polyhedron.... |
 3.3.3.5/2 Pentagrammic antiprism In geometry, the pentagrammic antiprism is one in an infinite set of nonconvex antiprisms formed by triangle sides and two regular star polygon caps, in this case two pentagrams.This polyhedron is identified with the indexed name U79 as a uniform polyhedron.... |
|||||
| d5d, [2+,5], (2*5) | 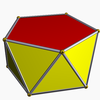 3.3.3.5 Pentagonal antiprism In geometry, the pentagonal antiprism is the third in an infinite set of antiprisms formed by an even-numbered sequence of triangle sides closed by two polygon caps. It consists of two pentagons joined to each other by a ring of 10 triangles for a total of 12 faces... |
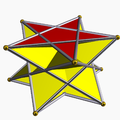 3.3.3.5/3 Pentagrammic crossed-antiprism In geometry, the pentagrammic crossed-antiprism is one in an infinite set of nonconvex antiprisms formed by triangle sides and two regular star polygon caps, in this case two pentagrams.... |
||||||
| d6h, [2,6], (*226) |  4.4.6 Hexagonal prism In geometry, the hexagonal prism is a prism with hexagonal base. The shape has 8 faces, 18 edges, and 12 vertices.Since it has eight faces, it is an octahedron. However, the term octahedron is primarily used to refer to the regular octahedron, which has eight triangular faces... |
|||||||
| d6d, [2+,6], (2*6) |  3.3.3.6 Hexagonal antiprism In geometry, the hexagonal antiprism is the 4th in an infinite set of antiprisms formed by an even-numbered sequence of triangle sides closed by two polygon caps.If faces are all regular, it is a semiregular polyhedron.- See also :* Set of antiprisms... |
|||||||
| d7h, [2,7], (*227) | 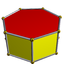 4.4.7 Heptagonal prism In geometry, the heptagonal prism is the fifth of the infinite set of convex prisms formed by square sides and two regular polygon caps, in this case two heptagons.... |
 4.4.7/2 |
 4.4.7/3 |
 3.3.3.7/2 |
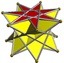 3.3.3.7/4 |
|||
| d7d, [2+,7], (2*7) |  3.3.3.7 Heptagonal antiprism In geometry, the heptagonal antiprism is the fourth in an infinite set of antiprisms formed by an even-numbered sequence of triangle sides closed by two polygon caps.If faces are all regular, it is a semiregular polyhedron.- See also :* Set of antiprisms... |
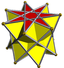 3.3.3.7/3 |
||||||
| d8h, [2,8], (*228) |  4.4.8 Octagonal prism In geometry, the octagonal prism is the sixth in an infinite set of prisms, formed by square sides and two regular octagon caps.If faces are all regular, it is a semiregular polyhedron.- Use :... |
 4.4.8/3 Octagrammic prism In geometry, the octagrammic prism is one of an infinite set of nonconvex prisms formed by rectangular sides and two regular star polygon caps, in this case two octagrams.An octagrammic prism's octagrammic bases may be in either form below:... |
||||||
| d8d, [2+,8], (2*8) | 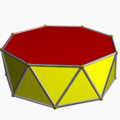 3.3.3.8 Octagonal antiprism In geometry, the octagonal antiprism is the 6th in an infinite set of antiprisms formed by an even-numbered sequence of triangle sides closed by two polygon caps.If faces are all regular, it is a semiregular polyhedron.- See also :* Set of antiprisms... |
 3.3.3.8/3 Octagrammic antiprism In geometry, the octagrammic antiprism is one in an infinite set of nonconvex antiprisms formed by triangle sides and two regular star polygon caps, in this case two octagrams.... |
 3.3.3.8/5 Octagrammic crossed-antiprism In geometry, the octagrammic crossed-antiprism is one in an infinite set of nonconvex antiprisms formed by triangle sides and two regular star polygon caps, in this case two octagrams.... |
|||||
| d9h, [2,9], (*229) |  4.4.9 |
 4.4.9/2 |
 4.4.9/4 |
 3.3.3.9/2 |
 3.3.3.9/4 |
|||
| d9d, [2+,9], (2*9) |  3.3.3.9 Enneagonal antiprism In geometry, the enneagonal antiprism is one in an infinite set of convex antiprisms formed by triangle sides and two regular polygon caps, in this case two enneagons.... |
 3.3.3.9/5 |
||||||
| d10h, [2,10], (*2.2.10) |  4.4.10 Decagonal prism In geometry, the decagonal prism is the eighth in an infinite set of prisms, formed by ten square side faces and two regular decagon caps. With twelve faces, it is one of many nonregular dodecahedra.If faces are all regular, it is a semiregular polyhedron.... |
 4.4.10/3 Decagrammic prism In geometry, the decagrammic prism is one of an infinite set of nonconvex prisms formed by squares sides and two regular star polygon caps, in this case two decagrams.... |
||||||
| d10d, [2+,10], (2*10) |  3.3.3.10 Decagonal antiprism In geometry, the decagonal antiprism is the eighth in an infinite set of antiprisms formed by an even-numbered sequence of triangle sides closed by two polygon caps.If faces are all regular, it is a semiregular polyhedron.- External links :*... |
 3.3.3.10/3 Decagrammic antiprism In geometry, the decagrammic antiprism is one in an infinite set of nonconvex antiprisms formed by triangle sides and two regular star polygon caps, in this case two decagrams.... |
||||||
| d11h, [2,11], (*2.2.11) |  4.4.11 |
 4.4.11/2 |
 4.4.11/3 |
 4.4.11/4 |
 4.4.11/5 |
 3.3.3.11/2 |
 3.3.3.11/4 |
 3.3.3.11/6 |
| d11d, [2+,11], (2*11) |  3.3.3.11 |
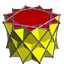 3.3.3.11/3 |
 3.3.3.11/5 |
 3.3.3.11/7 |
||||
| d12h, [2,12], (*2.2.12) |  4.4.12 Dodecagonal prism In geometry, the dodecagonal prism is the tenth in an infinite set of prisms, formed by square sides and two regular dodecagon caps.If faces are all regular, it is a semiregular polyhedron.- Use :... |
 4.4.12/5 |
||||||
| d12d, [2+,12], (2*12) |  3.3.3.12 Dodecagonal antiprism In geometry, the dodecagonal antiprism is the tenth in an infinite set of antiprisms formed by an even-numbered sequence of triangle sides closed by two polygon caps.If faces are all regular, it is a semiregular polyhedron.... |
 3.3.3.12/5 |
 3.3.3.12/7 |
|||||
| ... |
External links
- Prisms and Antiprisms George W. HartGeorge W. HartGeorge William Hart is a geometer who expresses himself both artistically and academically. He is also a research professor in the department of computer science at the State University of New York in Stony Brook, New York....

