Spherical symmetry groups are also called point groups in three dimensions

Point groups in three dimensions

In geometry, a point group in three dimensions is an isometry group in three dimensions that leaves the origin fixed, or correspondingly, an isometry group of a sphere. It is a subgroup of the orthogonal group O, the group of all isometries that leave the origin fixed, or correspondingly, the group...

, however this article is limitied to the finite symmetries.

There are five fundamental symmetry classes which have triangular fundamental domains: dihedral, cyclic, tetrahedral

Tetrahedral symmetry

150px|right|thumb|A regular [[tetrahedron]], an example of a solid with full tetrahedral symmetryA regular tetrahedron has 12 rotational symmetries, and a symmetry order of 24 including transformations that combine a reflection and a rotation.The group of all symmetries is isomorphic to the group...

, octahedral

Octahedral symmetry

150px|thumb|right|The [[cube]] is the most common shape with octahedral symmetryA regular octahedron has 24 rotational symmetries, and a symmetry order of 48 including transformations that combine a reflection and a rotation...

, and icosahedral

Icosahedral symmetry

A regular icosahedron has 60 rotational symmetries, and a symmetry order of 120 including transformations that combine a reflection and a rotation...

 symmetry.

This article lists the groups by Schoenflies notation

Schoenflies notation

The Schoenflies notation or Schönflies notation, named after the German mathematician Arthur Moritz Schoenflies, is one of two conventions commonly used to describe Point groups. This notation is used in spectroscopy. The other convention is the Hermann–Mauguin notation, also known as the...

, Coxeter notation

Coxeter notation

In geometry, Coxeter notation is a system of classifying symmetry groups, describing the angles between with fundamental reflections of a Coxeter group. It uses a bracketed notation, with modifiers to indicate certain subgroups. The notation is named after H. S. M...

, orbifold notation, and order. John Conway

John Horton Conway

John Horton Conway is a prolific mathematician active in the theory of finite groups, knot theory, number theory, combinatorial game theory and coding theory...

 uses a variation of the Schoenflies notation, named by one or two upper case letters, and whole number subscripts. The group order is defined as the subscript, unless the order is doubled for symbols with a plus or minus, "±", prefix.

Hermann–Mauguin notation (International notation) is also given. The crystallography

Crystallography

Crystallography is the experimental science of the arrangement of atoms in solids. The word "crystallography" derives from the Greek words crystallon = cold drop / frozen drop, with its meaning extending to all solids with some degree of transparency, and grapho = write.Before the development of...

 groups, 32 in total, are a subset with element orders 2, 3, 4 and 6.

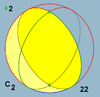
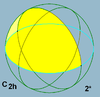
Involutional symmetry

There are four involutional groups: no symmetry, reflection symmetry

Reflection symmetry

Reflection symmetry, reflectional symmetry, line symmetry, mirror symmetry, mirror-image symmetry, or bilateral symmetry is symmetry with respect to reflection. That is, a figure which does not change upon undergoing a reflection has reflectional symmetry.In 2D there is a line of symmetry, in 3D a...

, 2-fold rotational symmetry, and central point symmetry.

Intl Geo Orbifold Schönflies Conway John Horton Conway John Horton Conway is a prolific mathematician active in the theory of finite groups, knot theory, number theory, combinatorial game theory and coding theory... Coxeter Coxeter notation In geometry, Coxeter notation is a system of classifying symmetry groups, describing the angles between with fundamental reflections of a Coxeter group. It uses a bracketed notation, with modifiers to indicate certain subgroups. The notation is named after H. S. M... Order Fundamental domain Fundamental domain In geometry, the fundamental domain of a symmetry group of an object is a part or pattern, as small or irredundant as possible, which determines the whole object based on the symmetry. More rigorously, given a topological space and a group acting on it, the images of a single point under the group... 1 1 C1 C1 [ ]+ 1 2 22 D1 = C2 D2 = C2 [2]+ 2

Intl Geo Orbifold Schönflies Conway Coxeter Order Fundamental domain × Ci = S2 CC2 [2+,2+] 2 = m 1 * Cs = C1v = C1h ±C1 = CD2 [ ] 2

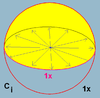
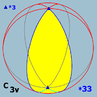
Cyclic symmetry

There are four infinite cyclic symmetry

Cyclic symmetries

This article deals with the four infinite series of point groups in three dimensions with n-fold rotational symmetry about one axis , and no other rotational symmetry :Chiral:*Cn of order n - n-fold rotational symmetry...

 families, with n=2 or higher. (n may be 1 as a special case)

Intl Geo Orbifold Schönflies Conway Coxeter Order Fundamental domain 2 22 C2 = D1 C2 = D2 [2]+ 2 mm2 2 *22 C2v = D1h CD4 = DD4 [2] 4 2× S4 CC4 [2+,4+] 4 2/m 2 2* C2h = D1d ±C2 = ±D2 [2,2+] 4

Intl Geo Orbifold Schönflies Conway Coxeter Order Fundamental domain 3 4 5 6 n 33 44 55 66 nn C3 C4 C5 C6 Cn C3 C4 C5 C6 Cn [3]+ [4]+ [5]+ [6]+ [n]+ 3 4 5 6 n 3m 4mm 5m 6mm - 3 4 5 6 n *33 *44 *55 *66 *nn C3v C4v C5v C6v Cnv CD6 CD8 CD10 CD12 CD2n [3] [4] [5] [6] [n] 6 8 10 12 2n - 3× 4× 5× 6× n× S6 S8 S10 S12 S2n ±C3 CC8 ±C5 CC12 CC2n / ±Cn [2+,6+] [2+,8+] [2+,10+] [2+,12+] [2+,2n+] 6 8 10 12 2n 3/m 4/m 5/m 6/m n/m 2 2 2 2 2 3* 4* 5* 6* n* C3h C4h C5h C6h Cnh CC6 ±C4 CC10 ±C6 ±Cn / CC2n [2,3+] [2,4+] [2,5+] [2,6+] [2,n+] 6 8 10 12 2n

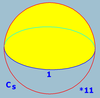
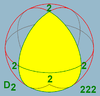
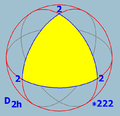
Dihedral symmetry

There are three infinite dihedral symmetry

Dihedral symmetry in three dimensions

This article deals with three infinite sequences of point groups in three dimensions which have a symmetry group that as abstract group is a dihedral group Dihn .See also point groups in two dimensions.Chiral:...

 families, with n as 2 or higher. (n may be 1 as a special case)

Intl Geo Orbifold Schönflies Conway Coxeter Order Fundamental domain 222 . 222 D2 D4 [2,2]+ 4 2m 4 2*2 D2d DD8 [2+,4] 8 mmm 22 *222 D2h ±D4 [2,2] 8

Intl Geo Orbifold Schönflies Conway Coxeter Order Fundamental domain 32 422 52 622 . . . . . 223 224 225 226 22n D3 D4 D5 D6 Dn D6 D8 D10 D12 D2n [2,3]+ [2,4]+ [2,5]+ [2,6]+ [2,n]+ 6 8 10 12 2n m 2m m .2m 6 8 10. 12. n 2*3 2*4 2*5 2*6 2*n D3d D4d D5d D6d Dnd ±D6 DD16 ±D10 DD24 DD4n / ±D2n [2+,6] [2+,8] [2+,10] [2+,12] [2+,2n] 12 16 20 24 4n m2 4/mmm m2 6/mmm 32 42 52 62 n2 *223 *224 *225 *226 *22n D3h D4h D5h D6h Dnh DD12 ±D8 DD20 ±D12 ±D2n / DD4n [2,3] [2,4] [2,5] [2,6] [2,n] 12 16 20 24 4n

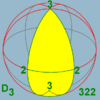
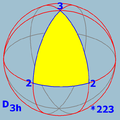
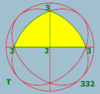
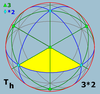
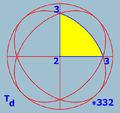
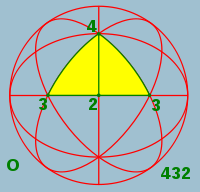
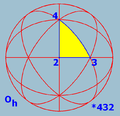
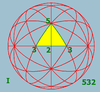
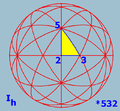
Polyhedral symmetry

There are three types of polyhedral symmetry: tetrahedral symmetry

Tetrahedral symmetry

150px|right|thumb|A regular [[tetrahedron]], an example of a solid with full tetrahedral symmetryA regular tetrahedron has 12 rotational symmetries, and a symmetry order of 24 including transformations that combine a reflection and a rotation.The group of all symmetries is isomorphic to the group...

, octahedral symmetry

Octahedral symmetry

150px|thumb|right|The [[cube]] is the most common shape with octahedral symmetryA regular octahedron has 24 rotational symmetries, and a symmetry order of 48 including transformations that combine a reflection and a rotation...

, and icosahedral symmetry

Icosahedral symmetry

A regular icosahedron has 60 rotational symmetries, and a symmetry order of 120 including transformations that combine a reflection and a rotation...

, named after the triangle-faced regular polyhedra with these symmetries.

[3,3] Intl Geo Orbifold Schönflies Conway Coxeter Order Fundamental domain 23 . 332 T T [3,3]+ = [3+,4,1+] 12 m 4 3*2 Th ±T [3+,4] = /nowiki>3,3]+] 24 3m 33 *332 Td TO [3,3] = [3,4,1+] 24

[3,4] Intl Geo Orbifold Schönflies Conway Coxeter Order Fundamental domain 432 . 432 O O [3,4]+ = 3,3+ 24 mm 43 *432 Oh ±O [3,4] = 3,3 48 [3,5] Intl Geo Orbifold Schönflies Conway Coxeter Order Fundamental domain 532 . 532 I I [3,5]+ 60 2/m 53 *532 Ih ±I [3,5] 120

See also

• Crystallographic point group
  Crystallographic point group
  In crystallography, a crystallographic point group is a set of symmetry operations, like rotations or reflections, that leave a central point fixed while moving other directions and faces of the crystal to the positions of features of the same kind...
  
  
• Triangle group
  Triangle group
  In mathematics, a triangle group is a group that can be realized geometrically by sequences of reflections across the sides of a triangle. The triangle can be an ordinary Euclidean triangle, a triangle on the sphere, or a hyperbolic triangle...
  
  
• List of planar symmetry groups

External links

• Finite spherical symmetry groups
• Simplest Canonical Polyhedra of Each Symmetry Type, by David I. McCooey