This article deals with the four infinite series of point groups in three dimensions

Point groups in three dimensions

In geometry, a point group in three dimensions is an isometry group in three dimensions that leaves the origin fixed, or correspondingly, an isometry group of a sphere. It is a subgroup of the orthogonal group O, the group of all isometries that leave the origin fixed, or correspondingly, the group...

 (n≥1) with n-fold rotational symmetry

Rotational symmetry

Generally speaking, an object with rotational symmetry is an object that looks the same after a certain amount of rotation. An object may have more than one rotational symmetry; for instance, if reflections or turning it over are not counted, the triskelion appearing on the Isle of Man's flag has...

about one axis (rotation

Rotation

A rotation is a circular movement of an object around a center of rotation. A three-dimensional object rotates always around an imaginary line called a rotation axis. If the axis is within the body, and passes through its center of mass the body is said to rotate upon itself, or spin. A rotation...

 by an angle of 360°/n does not change the object), and no other rotational symmetry (n=1 covers the cases of no rotational symmetry at all):

Chiral:

• C_n (nn) of order n - n-fold rotational symmetry (abstract group C_n
  Cyclic group
  In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
  
  ); for n=1: no symmetry (trivial group)

Achiral:

• C_nh (n*) of order 2n - prismatic symmetry (abstract group C_n
  Cyclic group
  In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
  
   × C₂); for n=1 this is denoted by C_s (1*) and called reflection symmetry
  Reflection symmetry
  Reflection symmetry, reflectional symmetry, line symmetry, mirror symmetry, mirror-image symmetry, or bilateral symmetry is symmetry with respect to reflection. That is, a figure which does not change upon undergoing a reflection has reflectional symmetry.In 2D there is a line of symmetry, in 3D a...
  
  , also bilateral symmetry.
• C_nv (*nn) of order 2n - pyramidal symmetry (abstract group D_n); in biology C_2v is called biradial symmetry. For n=1 we have again C_s (1*).
• S_2n (n×) of order 2n (not to be confused with symmetric group
  Symmetric group
  In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
  
  s, for which the same notation is used; abstract group C_2n); for n=1 we have S₂ (1×), also denoted by C_i; this is inversion symmetry

They are the finite symmetry group

Symmetry group

The symmetry group of an object is the group of all isometries under which it is invariant with composition as the operation...

s on a cone

Cone (geometry)

A cone is an n-dimensional geometric shape that tapers smoothly from a base to a point called the apex or vertex. Formally, it is the solid figure formed by the locus of all straight line segments that join the apex to the base...

. For n = they correspond to four frieze group

Frieze group

A frieze group is a mathematical concept to classify designs on two-dimensional surfaces which are repetitive in one direction, based on the symmetries in the pattern. Such patterns occur frequently in architecture and decorative art...

s. Schönflies

Arthur Moritz Schönflies

Arthur Moritz Schoenflies , sometimes written as Schönflies, was a German mathematician, known for his contributions to the application of group theory to crystallography, and for work in topology....

 notation is used, and, in parentheses, orbifold notation. The terms horizontal (h) and vertical (v) are used with respect to a vertical axis of rotation.

C_nh (n*) has reflection symmetry

Reflection symmetry

Reflection symmetry, reflectional symmetry, line symmetry, mirror symmetry, mirror-image symmetry, or bilateral symmetry is symmetry with respect to reflection. That is, a figure which does not change upon undergoing a reflection has reflectional symmetry.In 2D there is a line of symmetry, in 3D a...

 with respect to a plane perpendicular to the n-fold rotation axis.

C_nv (*nn) has vertical mirror planes. This is the symmetry group for a regular n-sided pyramid

Pyramid

A pyramid is a structure whose outer surfaces are triangular and converge at a single point. The base of a pyramid can be trilateral, quadrilateral, or any polygon shape, meaning that a pyramid has at least three triangular surfaces...

.

S_2n (n×) has a 2n-fold rotoreflection

Improper rotation

In 3D geometry, an improper rotation, also called rotoreflection or rotary reflection is, depending on context, a linear transformation or affine transformation which is the combination of a rotation about an axis and a reflection in a plane perpendicular to the axis.Equivalently it is the...

 axis, also called 2n-fold improper rotation axis, i.e., the symmetry group contains a combination of a reflection in the horizontal plane and a rotation by an angle 180°/n. Thus, like D_nd, it contains a number of improper rotations without containing the corresponding rotations.

C_2h (2*) and C_2v (*22) of order 4 are two of the three 3D symmetry group types with the Klein four-group

Klein four-group

In mathematics, the Klein four-group is the group Z2 × Z2, the direct product of two copies of the cyclic group of order 2...

 as abstract group. C_2v applies e.g. for a rectangular tile with its top side different from its bottom side.

Examples

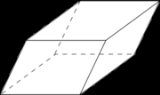
S2/Ci (1x):	C4v (*44):		C5v (*55):
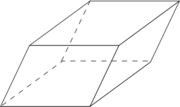Parallelepiped Parallelepiped In geometry, a parallelepiped is a three-dimensional figure formed by six parallelograms. By analogy, it relates to a parallelogram just as a cube relates to a square. In Euclidean geometry, its definition encompasses all four concepts...	Square pyramid Square pyramid In geometry, a square pyramid is a pyramid having a square base. If the apex is perpendicularly above the center of the square, it will have C4v symmetry.- Johnson solid :...	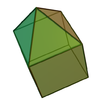Elongated square pyramid Elongated square pyramid In geometry, the elongated square pyramid is one of the Johnson solids . As the name suggests, it can be constructed by elongating a square pyramid by attaching a cube to its square base...	Pentagonal pyramid Pentagonal pyramid In geometry, a pentagonal pyramid is a pyramid with a pentagonal base upon which are erected five triangular faces that meet at a point . Like any pyramid, it is self-dual....