
Pentagonal pyramid
Encyclopedia
In geometry
, a pentagonal pyramid is a pyramid
with a pentagon
al base upon which are erected five triangular
faces that meet at a point (the vertex). Like any pyramid
, it is self-dual
.
The regular pentagonal pyramid has a base that is a regular pentagon and lateral faces that are equilateral triangles. It is one of the Johnson solid
s (J2). Its height H, from the midpoint of the pentagonal face to the apex, (as a function of a, where a is the side length), can be computed as: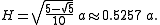
Its surface area, A, can be computed as the area of pentagonal base plus five times the area of one triangle: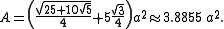
Its volume when an edge length is known can be figured out with this formula: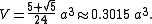
It can be seen as the "lid" of an icosahedron
; the rest of the icosahedron forms a gyroelongated pentagonal pyramid
, J11. The 92 Johnson solids were named and described by Norman Johnson in 1966.
More generally an order-2 vertex-uniform pentagonal pyramid can be defined with a regular pentagonal base and 5 isosceles triangle sides of any height.
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, a pentagonal pyramid is a pyramid
Pyramid (geometry)
In geometry, a pyramid is a polyhedron formed by connecting a polygonal base and a point, called the apex. Each base edge and apex form a triangle. It is a conic solid with polygonal base....
with a pentagon
Pentagon
In geometry, a pentagon is any five-sided polygon. A pentagon may be simple or self-intersecting. The sum of the internal angles in a simple pentagon is 540°. A pentagram is an example of a self-intersecting pentagon.- Regular pentagons :In a regular pentagon, all sides are equal in length and...
al base upon which are erected five triangular
Triangle
A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....
faces that meet at a point (the vertex). Like any pyramid
Pyramid
A pyramid is a structure whose outer surfaces are triangular and converge at a single point. The base of a pyramid can be trilateral, quadrilateral, or any polygon shape, meaning that a pyramid has at least three triangular surfaces...
, it is self-dual
Dual polyhedron
In geometry, polyhedra are associated into pairs called duals, where the vertices of one correspond to the faces of the other. The dual of the dual is the original polyhedron. The dual of a polyhedron with equivalent vertices is one with equivalent faces, and of one with equivalent edges is another...
.
The regular pentagonal pyramid has a base that is a regular pentagon and lateral faces that are equilateral triangles. It is one of the Johnson solid
Johnson solid
In geometry, a Johnson solid is a strictly convex polyhedron, each face of which is a regular polygon, but which is not uniform, i.e., not a Platonic solid, Archimedean solid, prism or antiprism. There is no requirement that each face must be the same polygon, or that the same polygons join around...
s (J2). Its height H, from the midpoint of the pentagonal face to the apex, (as a function of a, where a is the side length), can be computed as:
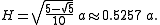
Its surface area, A, can be computed as the area of pentagonal base plus five times the area of one triangle:
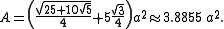
Its volume when an edge length is known can be figured out with this formula:
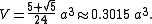
It can be seen as the "lid" of an icosahedron
Icosahedron
In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids....
; the rest of the icosahedron forms a gyroelongated pentagonal pyramid
Gyroelongated pentagonal pyramid
In geometry, the gyroelongated pentagonal pyramid is one of the Johnson solids . As its name suggests, it is formed by taking a pentagonal pyramid and "gyroelongating" it, which in this case involves joining a pentagonal antiprism to its base....
, J11. The 92 Johnson solids were named and described by Norman Johnson in 1966.
More generally an order-2 vertex-uniform pentagonal pyramid can be defined with a regular pentagonal base and 5 isosceles triangle sides of any height.
Related polyhedra
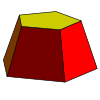 Pentagonal frustum Frustum In geometry, a frustum is the portion of a solid that lies between two parallel planes cutting it.... is a pentagonal pyramid with its apex truncated |
 The vertex of an icosahedron Icosahedron In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids.... is a pentagonal pyramid |
Dual polyhedron
The pentagonal pyramid is topologically a self-dual polyhedron. The dual edge lengths are different due to the polar reciprocation.| Dual pentagonal pyramid | Net of dual |
|---|---|
External links
- Virtual Reality Polyhedra www.georgehart.com: The Encyclopedia of Polyhedra ( VRMLVRMLVRML is a standard file format for representing 3-dimensional interactive vector graphics, designed particularly with the World Wide Web in mind...
model)

