
Uniform polyteron
Encyclopedia
5-simplex |
Rectified 5-simplex |
Truncated 5-simplex |
|||||||||
Cantellated 5-simplex |
Runcinated 5-simplex Runcinated 5-simplex In six-dimensional geometry, a runcinated 5-simplex is a convex uniform 5-polytope with 3rd order truncations of the regular 5-simplex.There are 4 unique runcinations of the 5-simplex with permutations of truncations, and cantellations.... |
Stericated 5-simplex |
|||||||||
5-orthoplex |
Truncated 5-orthoplex Truncated 5-orthoplex In six-dimensional geometry, a truncated 5-orthoplex is a convex uniform 5-polytope, being a truncation of the regular 5-orthoplex.There are 4 unique truncations of the 5-orthoplex. Vertices of the truncation 5-orthoplex are located as pairs on the edge of the 5-orthoplex. Vertices of the... |
Rectified 5-orthoplex |
|||||||||
Cantellated 5-orthoplex Cantellated 5-orthoplex In six-dimensional geometry, a cantellated 5-orthoplex is a convex uniform 5-polytope, being a cantellation of the regular 5-orthoplex.There are 6 cantellation for the 5-orthoplex, including truncations... |
Runcinated 5-orthoplex Runcinated 5-orthoplex In six-dimensional geometry, a runcinated 5-orthoplex is a convex uniform 5-polytope with 3rd order truncation of the regular 5-orthoplex.There are 8 runcinations of the 5-orthoplex with permutations of truncations, and cantellations... |
||||||||||
Cantellated 5-cube Cantellated 5-cube In six-dimensional geometry, a cantellated 5-cube is a convex uniform 5-polytope, being a cantellation of the regular 5-cube.There are 6 unique cantellation for the 5-cube, including truncations... |
Runcinated 5-cube Runcinated 5-cube In five-dimensional geometry, a runcinated 5-cube is a convex uniform 5-polytope that is a runcination of the regular 5-cube.... |
Stericated 5-cube Stericated 5-cube In five-dimensional geometry, a stericated 5-cube is a convex uniform 5-polytope with fourth-order truncations of the regular 5-cube.... |
|||||||||
5-cube |
Truncated 5-cube Truncated 5-cube In five-dimensional geometry, a truncated 5-cube is a convex uniform 5-polytope, being a truncation of the regular 5-cube.There are four unique truncations of the 5-cube. Vertices of the truncated 5-cube are located as pairs on the edge of the 5-cube. Vertices of the bitruncated 5-cube are located... |
Rectified 5-cube Rectified 5-cube In give-dimensional geometry, a rectified 5-cube is a convex uniform 5-polytope, being a rectification of the regular 5-cube.There are 5 degrees of rectifications of a 5-polytope, the zeroth here being the 5-cube, and the 4th and last being the 5-orthoplex. Vertices of the rectified 5-cube are... |
|||||||||
5-demicube |
Truncated 5-demicube |
||||||||||
Cantellated 5-demicube Cantellated 5-demicube In six-dimensional geometry, a cantellated 5-demicube is a convex uniform 5-polytope, being a cantellation of the uniform 5-demicube.There are 2 unique cantellation for the 5-demicube including a truncation.- Cantellated 5-demicube:... |
Runcinated 5-demicube Runcinated 5-demicube In five-dimensional geometry, a runcinated 5-demicube is a convex uniform 5-polytope with a runcination operation, a 3rd order truncations the uniform 5-demicube.... |
||||||||||
In geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, a uniform polyteron (or uniform 5-polytope
5-polytope
In five-dimensional geometry, a 5-polytope is a 5-dimensional polytope, bounded by facets. Each polyhedral cell being shared by exactly two polychoron facets. A proposed name for 5-polytopes is polyteron.-Definition:...
) is a five-dimensional uniform polytope
Uniform polytope
A uniform polytope is a vertex-transitive polytope made from uniform polytope facets of a lower dimension. Uniform polytopes of 2 dimensions are the regular polygons....
. By definition, a uniform polyteron is vertex-transitive
Vertex-transitive
In geometry, a polytope is isogonal or vertex-transitive if, loosely speaking, all its vertices are the same...
and constructed from uniform polychoron
Uniform polychoron
In geometry, a uniform polychoron is a polychoron or 4-polytope which is vertex-transitive and whose cells are uniform polyhedra....
facets.
The complete set of convex uniform polytera has not been determined, but most can be made as Wythoff construction
Wythoff construction
In geometry, a Wythoff construction, named after mathematician Willem Abraham Wythoff, is a method for constructing a uniform polyhedron or plane tiling. It is often referred to as Wythoff's kaleidoscopic construction.- Construction process :...
s from a small set of symmetry groups. These construction operations are represented by the permutations of rings of the Coxeter-Dynkin diagram
Coxeter-Dynkin diagram
In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors...
s.
Regular 5-polytopes
Regular 5-polytopes can be represented by the Schläfli symbol {p,q,r,s}, with s {p,q,r} polychoral facetsFacet (mathematics)
A facet of a simplicial complex is a maximal simplex.In the general theory of polyhedra and polytopes, two conflicting meanings are currently jostling for acceptability:...
around each face
Face (geometry)
In geometry, a face of a polyhedron is any of the polygons that make up its boundaries. For example, any of the squares that bound a cube is a face of the cube...
. There are exactly three such regular polytopes, all convex:
- {3,3,3,3} - HexateronHexateronIn five dimensional geometry, a 5-simplex is a self-dual regular 5-polytope. It has 6 vertices, 15 edges, 20 triangle faces, 15 tetrahedral cells, and 6 pentachoron facets. It has a dihedral angle of cos−1, or approximately 78.46°.- Alternate names :...
(5-simplexSimplexIn geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...
) - {4,3,3,3} - PenteractPenteractIn five dimensional geometry, a 5-cube is a name for a five dimensional hypercube with 32 vertices, 80 edges, 80 square faces, 40 cubic cells, and 10 tesseract hypercells....
(5-hypercubeHypercubeIn geometry, a hypercube is an n-dimensional analogue of a square and a cube . It is a closed, compact, convex figure whose 1-skeleton consists of groups of opposite parallel line segments aligned in each of the space's dimensions, perpendicular to each other and of the same length.An...
) - {3,3,3,4} - PentacrossPentacrossIn five-dimensional geometry, a 5-orthoplex, or 5-cross polytope, is a five-dimensional polytope with 10 vertices, 40 edges, 80 triangle faces, 80 tetrahedron cells, 32 5-cell hypercells....
(5-orthoplex)
There are no nonconvex regular polytopes in 5 or more dimensions.
Convex uniform 5-polytopes
There are 105 known convex uniform 5-polytopes, plus a number of infinite families of duoprism prisms, and polygon-polyhedron duoprisms. All except the grand antiprism prism are based on Wythoff constructionWythoff construction
In geometry, a Wythoff construction, named after mathematician Willem Abraham Wythoff, is a method for constructing a uniform polyhedron or plane tiling. It is often referred to as Wythoff's kaleidoscopic construction.- Construction process :...
s, reflection symmetry generated with Coxeter group
Coxeter group
In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example...
s.
Reflection families
The hexateronHexateron
In five dimensional geometry, a 5-simplex is a self-dual regular 5-polytope. It has 6 vertices, 15 edges, 20 triangle faces, 15 tetrahedral cells, and 6 pentachoron facets. It has a dihedral angle of cos−1, or approximately 78.46°.- Alternate names :...
is the regular form in the A5 family. The penteract and pentacross are the regular forms in the B5 family. The bifurcating graph of the D6 family contains the pentacross, as well as a demipenteract
Demipenteract
In five dimensional geometry, a demipenteract or 5-demicube is a semiregular 5-polytope, constructed from a 5-hypercube with alternated vertices deleted.It was discovered by Thorold Gosset...
which is an alternated penteract.
Fundamental families
| # | Coxeter group Coxeter group In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example... |
Coxeter-Dynkin diagram Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... |
|
|---|---|---|---|
| 1 | A5 | [34] | |
| 2 | B5 | [4,33] | |
| 3 | D5 | [32,1,1] |
Uniform prisms
There are 5 finite categorical uniform
Uniform polytope
A uniform polytope is a vertex-transitive polytope made from uniform polytope facets of a lower dimension. Uniform polytopes of 2 dimensions are the regular polygons....
prismatic families of polytopes based on the nonprismatic uniform 4-polytopes:
| # | Coxeter group Coxeter group In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example... s |
Coxeter graph Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... |
|
|---|---|---|---|
| 1 | A4 × A1 | [3,3,3] × [ ] | |
| 2 | B4 × A1 | [4,3,3] × [ ] | |
| 3 | F4 × A1 | [3,4,3] × [ ] | |
| 4 | H4 × A1 | [5,3,3] × [ ] | |
| 5 | D4 × A1 | [31,1,1] × [ ] |
There is one infinite family of 5-polytopes based on prisms of the uniform duoprism
Duoprism
In geometry of 4 dimensions or higher, a duoprism is a polytope resulting from the Cartesian product of two polytopes, each of two dimensions or higher...
s {p}×{q}×{ }:
| Coxeter group Coxeter group In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example... s |
Coxeter graph Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... |
|
|---|---|---|
| I2(p) × I2(q) × A1 | [p] × [q] × [ ] |
Uniform duoprisms
There are 3 categorical uniform
Uniform polytope
A uniform polytope is a vertex-transitive polytope made from uniform polytope facets of a lower dimension. Uniform polytopes of 2 dimensions are the regular polygons....
duoprism
Duoprism
In geometry of 4 dimensions or higher, a duoprism is a polytope resulting from the Cartesian product of two polytopes, each of two dimensions or higher...
atic families of polytopes based on Cartesian product
Cartesian product
In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
s of the uniform polyhedra
Uniform polyhedron
A uniform polyhedron is a polyhedron which has regular polygons as faces and is vertex-transitive...
and regular polygon
Regular polygon
A regular polygon is a polygon that is equiangular and equilateral . Regular polygons may be convex or star.-General properties:...
s: {q,r}×{p}:
| # | Coxeter group Coxeter group In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example... s |
Coxeter graph Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... |
|
|---|---|---|---|
| 1 | A3 × I2(p) | [3,3] × [p] | |
| 2 | B3 × I2(p) | [4,3] × [p] | |
| 3. | H3 × I2(p) | [5,3] × [p] |
Enumerating the convex uniform 5-polytopes
- SimplexSimplexIn geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...
family: A5 [34]- 19 uniform 5-polytopes
- HypercubeHypercubeIn geometry, a hypercube is an n-dimensional analogue of a square and a cube . It is a closed, compact, convex figure whose 1-skeleton consists of groups of opposite parallel line segments aligned in each of the space's dimensions, perpendicular to each other and of the same length.An...
/Orthoplex family: BC5 [4,33]- 31 uniform 5-polytopes
- Demihypercube D5/E5 family: [32,1,1]
- 23 uniform 5-polytopes (8 unique)
- Prisms and duoprisms:
- 56 uniform 5-polytope (46 unique) constructions based on prismatic families: [3,3,3]x[ ], [4,3,3]x[ ], [5,3,3]x[ ], [31,1,1]x[ ].
- One non-Wythoffian - The grand antiprism prism is the only known non-Wythoffian convex uniform 5-polytope, constructed from two grand antiprismGrand antiprismIn geometry, the grand antiprism or pentagonal double antiprismoid is a uniform polychoron bounded by 320 cells: 20 pentagonal antiprisms, and 300 tetrahedra. It is an anomalous, non-Wythoffian uniform polychoron, discovered in 1965 by Conway and Guy.- Alternate names :* Pentagonal double...
s connected by polyhedral prisms.
That brings the tally to: 19+31+8+46+1=105
In addition there are:
- Infinitely many uniform 5-polytope constructions based on duoprism prismatic families: [p]x[q]x[ ].
- Infinitely many uniform 5-polytope constructions based on duoprismatic families: [3,3]x[p], [4,3]x[p], [5,3]x[p].
The A5 family
There are 19 forms based on all permutations of the Coxeter-Dynkin diagramCoxeter-Dynkin diagram
In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors...
s with one or more rings. (16+4-1 cases)
They are named by Norman Johnson from the Wythoff construction operations upon regular 5-simplex (hexateron).
The A5 family has symmetry of order 720 (6 factorial
Factorial
In mathematics, the factorial of a non-negative integer n, denoted by n!, is the product of all positive integers less than or equal to n...
).
The coordinates of uniform 5-polytopes with 5-simplex symmetry can be generated as permutations of simple integers in 6-space, all in hyperplanes with normal vector (1,1,1,1,1,1).
See symmetry graphs: List of A5 polytopes
| # | Base point | Johnson naming system Bowers name and (acronym) Coxeter-Dynkin Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... |
k-face element counts | Vertex figure Vertex figure In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:... |
Facet counts by location: [3,3,3,3] | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 4 | 3 | 2 | 1 | 0 | [3,3,3] (6) |
[3,3]×[ ] (15) |
[3]×[3] (20) |
[ ]×[3,3] (15) |
[3,3,3] (6) |
||||
| 1 | (0,0,0,0,0,1) or (0,1,1,1,1,1) | 5-simplex hexateron (hix) |
6 | 15 | 20 | 15 | 6 | 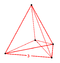 {3,3,3} |
(5) {3,3,3} |
- | - | - | - |
| 2 | (0,0,0,0,1,1) or (0,0,1,1,1,1) | Rectified 5-simplex rectified hexateron (rix) |
12 | 45 | 80 | 60 | 15 | 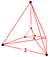 t{3,3}x{ } Truncated tetrahedral prism In geometry, a truncated tetrahedral prism is a convex uniform polychoron . This polychoron has 10 polyhedral cells: 2 truncated tetrahedra connected by 4 triangular prisms and 4 hexagonal prisms. It has 24 faces: 8 triangular, 18 square, and 8 hexagons. It has 48 edges and 24 vertices.Alternative... |
(4) t1{3,3,3} Rectified 5-cell In four dimensional geometry, the rectified 5-cell is a uniform polychoron composed of 5 regular tetrahedral and 5 regular octahedral cells. Each edge has one tetrahedron and two octahedra. Each vertex has two tetrahedra and three octahedra. In total it has 30 triangle faces, 30 edges, and 10... |
- | - | - | (2) {3,3,3} |
| 3 | (0,0,0,0,1,2) or (0,1,2,2,2,2) | Truncated 5-simplex truncated hexateron (tix) |
12 | 60 | 120 | 90 | 20 | 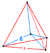 Tetrah.pyr |
(4) t0,1{3,3,3} Truncated 5-cell In geometry, a truncated 5-cell is a uniform polychoron formed as the truncation of the regular 5-cell.There are two degrees of trunctions, including a bitruncation.- Truncated 5-cell:... |
- | - | - | (1) {3,3,3} |
| 4 | (0,0,0,1,1,1) | Birectified 5-simplex dodecateron (dot) |
12 | 45 | 80 | 75 | 30 | 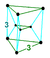 {3}x{3} Duoprism In geometry of 4 dimensions or higher, a duoprism is a polytope resulting from the Cartesian product of two polytopes, each of two dimensions or higher... |
(3) t1{3,3,3} Rectified 5-cell In four dimensional geometry, the rectified 5-cell is a uniform polychoron composed of 5 regular tetrahedral and 5 regular octahedral cells. Each edge has one tetrahedron and two octahedra. Each vertex has two tetrahedra and three octahedra. In total it has 30 triangle faces, 30 edges, and 10... |
- | - | - | (3) t1{3,3,3} Rectified 5-cell In four dimensional geometry, the rectified 5-cell is a uniform polychoron composed of 5 regular tetrahedral and 5 regular octahedral cells. Each edge has one tetrahedron and two octahedra. Each vertex has two tetrahedra and three octahedra. In total it has 30 triangle faces, 30 edges, and 10... |
| 5 | (0,0,0,1,1,2) or (0,1,1,2,2,2) | Cantellated 5-simplex small rhombated hexateron (sarx) |
12 | 60 | 140 | 150 | 60 |  prism-wedge |
(3) t0,2{3,3,3} Cantellated 5-cell In four-dimensional geometry, a cantellated 5-cell is a convex uniform polychoron, being a cantellation of the regular 5-cell.There are 2 unique degrees of runcinations of the 5-cell including with permutations truncations.... |
- | - | (1) × { }×{3,3} |
(1) t1{3,3,3} Rectified 5-cell In four dimensional geometry, the rectified 5-cell is a uniform polychoron composed of 5 regular tetrahedral and 5 regular octahedral cells. Each edge has one tetrahedron and two octahedra. Each vertex has two tetrahedra and three octahedra. In total it has 30 triangle faces, 30 edges, and 10... |
| 6 | (0,0,0,1,2,2) or (0,0,1,2,2,2) | Bitruncated 5-simplex bitruncated hexateron (bittix) |
27 | 135 | 290 | 240 | 60 |  |
(3) t1,2{3,3,3} |
- | - | - | (2) t0,1{3,3,3} Truncated 5-cell In geometry, a truncated 5-cell is a uniform polychoron formed as the truncation of the regular 5-cell.There are two degrees of trunctions, including a bitruncation.- Truncated 5-cell:... |
| 7 | (0,0,0,1,2,3) or (0,1,2,3,3,3) | Cantitruncated 5-simplex great rhombated hexateron (garx) |
32 | 180 | 420 | 360 | 90 | t0,1,2{3,3,3} |
- | - | × { }×{3,3} |
t0,1{3,3,3} Truncated 5-cell In geometry, a truncated 5-cell is a uniform polychoron formed as the truncation of the regular 5-cell.There are two degrees of trunctions, including a bitruncation.- Truncated 5-cell:... |
|
| 8 | (0,0,1,1,1,2) or (0,1,1,1,2,2) | Runcinated 5-simplex Runcinated 5-simplex In six-dimensional geometry, a runcinated 5-simplex is a convex uniform 5-polytope with 3rd order truncations of the regular 5-simplex.There are 4 unique runcinations of the 5-simplex with permutations of truncations, and cantellations.... small prismated hexateron (spix) |
47 | 255 | 420 | 270 | 60 |  |
(2) t0,3{3,3,3} |
- | (3) × {3}×{3} Duoprism In geometry of 4 dimensions or higher, a duoprism is a polytope resulting from the Cartesian product of two polytopes, each of two dimensions or higher... |
(3) × { }×t1{3,3} Octahedral prism In geometry, a octahedral prism is a convex uniform polychoron . This polychoron has 10 polyhedral cells: 2 octahedra connected by 8 triangular prisms.- Related polytopes :... |
(1) t1{3,3,3} Rectified 5-cell In four dimensional geometry, the rectified 5-cell is a uniform polychoron composed of 5 regular tetrahedral and 5 regular octahedral cells. Each edge has one tetrahedron and two octahedra. Each vertex has two tetrahedra and three octahedra. In total it has 30 triangle faces, 30 edges, and 10... |
| 9 | (0,0,1,1,2,2) | Bicantellated 5-simplex small birhombated dodecateron (sibrid) |
62 | 180 | 210 | 120 | 30 |  |
(2) t0,2{3,3,3} Cantellated 5-cell In four-dimensional geometry, a cantellated 5-cell is a convex uniform polychoron, being a cantellation of the regular 5-cell.There are 2 unique degrees of runcinations of the 5-cell including with permutations truncations.... |
- | (8) × {3}×{3} Duoprism In geometry of 4 dimensions or higher, a duoprism is a polytope resulting from the Cartesian product of two polytopes, each of two dimensions or higher... |
- | (2) t0,2{3,3,3} Cantellated 5-cell In four-dimensional geometry, a cantellated 5-cell is a convex uniform polychoron, being a cantellation of the regular 5-cell.There are 2 unique degrees of runcinations of the 5-cell including with permutations truncations.... |
| 10 | (0,0,1,1,2,3) or (0,1,2,2,3,3) | Runcitruncated 5-simplex prismatotruncated hexateron (pattix) |
27 | 135 | 290 | 300 | 120 | t0,1,3{3,3,3} |
- | × {6}×{3} Duoprism In geometry of 4 dimensions or higher, a duoprism is a polytope resulting from the Cartesian product of two polytopes, each of two dimensions or higher... |
× { }×t1{3,3} Octahedral prism In geometry, a octahedral prism is a convex uniform polychoron . This polychoron has 10 polyhedral cells: 2 octahedra connected by 8 triangular prisms.- Related polytopes :... |
t0,2{3,3,3} Cantellated 5-cell In four-dimensional geometry, a cantellated 5-cell is a convex uniform polychoron, being a cantellation of the regular 5-cell.There are 2 unique degrees of runcinations of the 5-cell including with permutations truncations.... |
|
| 11 | (0,0,1,2,2,3) or (0,1,1,2,3,3) | Runcicantellated 5-simplex prismatorhombated hexateron (pirx) |
32 | 180 | 420 | 450 | 180 | t0,1,3{3,3,3} |
- | × {3}×{3} Duoprism In geometry of 4 dimensions or higher, a duoprism is a polytope resulting from the Cartesian product of two polytopes, each of two dimensions or higher... |
× { }×t0,1{3,3} Truncated tetrahedral prism In geometry, a truncated tetrahedral prism is a convex uniform polychoron . This polychoron has 10 polyhedral cells: 2 truncated tetrahedra connected by 4 triangular prisms and 4 hexagonal prisms. It has 24 faces: 8 triangular, 18 square, and 8 hexagons. It has 48 edges and 24 vertices.Alternative... |
t1,2{3,3,3} |
|
| 12 | (0,0,1,2,3,3) | Bicantitruncated 5-simplex great birhombated dodecateron (gibrid) |
47 | 315 | 720 | 630 | 180 | t0,1,2{3,3,3} |
- | × {3}×{3} Duoprism In geometry of 4 dimensions or higher, a duoprism is a polytope resulting from the Cartesian product of two polytopes, each of two dimensions or higher... |
- | t0,1,2{3,3,3} |
|
| 13 | (0,0,1,2,3,4) or (0,1,2,3,4,4) | Runcicantitruncated 5-simplex great prismated hexateron (gippix) |
47 | 255 | 570 | 540 | 180 | Irr.5-cell |
t0,1,2,3{3,3,3} |
- | × {3}×{6} Duoprism In geometry of 4 dimensions or higher, a duoprism is a polytope resulting from the Cartesian product of two polytopes, each of two dimensions or higher... |
× { }×t0,1{3,3} Truncated tetrahedral prism In geometry, a truncated tetrahedral prism is a convex uniform polychoron . This polychoron has 10 polyhedral cells: 2 truncated tetrahedra connected by 4 triangular prisms and 4 hexagonal prisms. It has 24 faces: 8 triangular, 18 square, and 8 hexagons. It has 48 edges and 24 vertices.Alternative... |
t0,2{3,3,3} Cantellated 5-cell In four-dimensional geometry, a cantellated 5-cell is a convex uniform polychoron, being a cantellation of the regular 5-cell.There are 2 unique degrees of runcinations of the 5-cell including with permutations truncations.... |
| 14 | (0,1,1,1,1,2) | Stericated 5-simplex small cellated dodecateron (scad) |
62 | 330 | 570 | 420 | 120 |  Irr.16-cell 16-cell In four dimensional geometry, a 16-cell or hexadecachoron is a regular convex 4-polytope. It is one of the six regular convex 4-polytopes first described by the Swiss mathematician Ludwig Schläfli in the mid-19th century.... |
(1) {3,3,3} |
(4) × { }×{3,3} |
(6) × {3}×{3} Duoprism In geometry of 4 dimensions or higher, a duoprism is a polytope resulting from the Cartesian product of two polytopes, each of two dimensions or higher... |
(4) × { }×{3,3} |
(1) {3,3,3} |
| 15 | (0,1,1,1,2,3) or (0,1,2,2,2,3) | Steritruncated 5-simplex celliprismated hexateron (cappix) |
62 | 420 | 900 | 720 | 180 | t0,1{3,3,3} Truncated 5-cell In geometry, a truncated 5-cell is a uniform polychoron formed as the truncation of the regular 5-cell.There are two degrees of trunctions, including a bitruncation.- Truncated 5-cell:... |
× { }×t0,1{3,3} Truncated tetrahedral prism In geometry, a truncated tetrahedral prism is a convex uniform polychoron . This polychoron has 10 polyhedral cells: 2 truncated tetrahedra connected by 4 triangular prisms and 4 hexagonal prisms. It has 24 faces: 8 triangular, 18 square, and 8 hexagons. It has 48 edges and 24 vertices.Alternative... |
× {3}×{6} Duoprism In geometry of 4 dimensions or higher, a duoprism is a polytope resulting from the Cartesian product of two polytopes, each of two dimensions or higher... |
× { }×{3,3} |
t0,3{3,3,3} |
|
| 16 | (0,1,1,2,2,3) | Stericantellated 5-simplex small cellirhombated dodecateron (card) |
47 | 315 | 810 | 900 | 360 | t0,2{3,3,3} Cantellated 5-cell In four-dimensional geometry, a cantellated 5-cell is a convex uniform polychoron, being a cantellation of the regular 5-cell.There are 2 unique degrees of runcinations of the 5-cell including with permutations truncations.... |
× { }×t0,2{3,3} Cuboctahedral prism In geometry, a cuboctahedral prism is a convex uniform polychoron . This polychoron has 16 polyhedral cells: 2 cuboctahedra connected by 8 triangular prisms, and 6 cubes.... |
× {3}×{3} Duoprism In geometry of 4 dimensions or higher, a duoprism is a polytope resulting from the Cartesian product of two polytopes, each of two dimensions or higher... |
× { }×t0,2{3,3} Cuboctahedral prism In geometry, a cuboctahedral prism is a convex uniform polychoron . This polychoron has 16 polyhedral cells: 2 cuboctahedra connected by 8 triangular prisms, and 6 cubes.... |
t0,2{3,3,3} Cantellated 5-cell In four-dimensional geometry, a cantellated 5-cell is a convex uniform polychoron, being a cantellation of the regular 5-cell.There are 2 unique degrees of runcinations of the 5-cell including with permutations truncations.... |
|
| 17 | (0,1,1,2,3,4) or (0,1,2,3,3,4) | Stericantitruncated 5-simplex celligreatorhombated hexateron (cograx) |
62 | 480 | 1140 | 1080 | 360 | t0,1,2{3,3,3} |
× { }×t0,1,2{3,3} Truncated octahedral prism In 4-dimensional geometry, a truncated octahedral prism is a convex uniform polychoron . This polychoron has 16 cells It has 64 faces , and 96 edges and 48 vertices.It has two symmetry constructions, one from the truncated octahedron, and one as an omnitruncation of... |
× {3}×{6} Duoprism In geometry of 4 dimensions or higher, a duoprism is a polytope resulting from the Cartesian product of two polytopes, each of two dimensions or higher... |
× { }×t0,2{3,3} Cuboctahedral prism In geometry, a cuboctahedral prism is a convex uniform polychoron . This polychoron has 16 polyhedral cells: 2 cuboctahedra connected by 8 triangular prisms, and 6 cubes.... |
t0,1,3{3,3,3} |
|
| 18 | (0,1,2,2,3,4) | Steriruncitruncated 5-simplex celliprismatotruncated dodecateron (captid) |
62 | 450 | 1110 | 1080 | 360 | t0,1,3{3,3,3} |
× { }×t0,1{3,3} Truncated tetrahedral prism In geometry, a truncated tetrahedral prism is a convex uniform polychoron . This polychoron has 10 polyhedral cells: 2 truncated tetrahedra connected by 4 triangular prisms and 4 hexagonal prisms. It has 24 faces: 8 triangular, 18 square, and 8 hexagons. It has 48 edges and 24 vertices.Alternative... |
× {6}×{6} Duoprism In geometry of 4 dimensions or higher, a duoprism is a polytope resulting from the Cartesian product of two polytopes, each of two dimensions or higher... |
× { }×t0,1,3{3,3} Truncated tetrahedral prism In geometry, a truncated tetrahedral prism is a convex uniform polychoron . This polychoron has 10 polyhedral cells: 2 truncated tetrahedra connected by 4 triangular prisms and 4 hexagonal prisms. It has 24 faces: 8 triangular, 18 square, and 8 hexagons. It has 48 edges and 24 vertices.Alternative... |
t0,1,3{3,3,3} |
|
| 19 | (0,1,2,3,4,5) | Omnitruncated 5-simplex great cellated dodecateron (gocad) |
62 | 540 | 1560 | 1800 | 720 |  Irr. {3,3,3} |
(1) t0,1,2,3{3,3,3} |
(1) × { }×t0,1,2{3,3} Truncated octahedral prism In 4-dimensional geometry, a truncated octahedral prism is a convex uniform polychoron . This polychoron has 16 cells It has 64 faces , and 96 edges and 48 vertices.It has two symmetry constructions, one from the truncated octahedron, and one as an omnitruncation of... |
(1) × {6}×{6} Duoprism In geometry of 4 dimensions or higher, a duoprism is a polytope resulting from the Cartesian product of two polytopes, each of two dimensions or higher... |
(1) × { }×t0,1,2{3,3} Truncated octahedral prism In 4-dimensional geometry, a truncated octahedral prism is a convex uniform polychoron . This polychoron has 16 cells It has 64 faces , and 96 edges and 48 vertices.It has two symmetry constructions, one from the truncated octahedron, and one as an omnitruncation of... |
(1) t0,1,2,3{3,3,3} |
The B5 family
The B5 family has symmetry of order 3840 (5!×25).This family has 25−1=31 Wythoffian uniform polytopes generated by marking one or more nodes of the Coxeter-Dynkin diagram
Coxeter-Dynkin diagram
In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors...
.
For simplicity it is divided into two subgroups, each with 12 forms, and 7 "middle" forms which equally belong in both.
The penteractic family of polytera are given by the convex hulls of the base points listed in the following table, with all permutations of coordinates and sign taken. Each base point generates a distinct uniform polyteron. All coordinates correspond with uniform polytera of edge length 2.
See symmetry graph: List of B5 polytopes
| # | Base point | Name Coxeter-Dynkin Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... |
Element counts | Vertex figure Vertex figure In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:... |
Facet counts by location: [4,3,3,3] | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 4 | 3 | 2 | 1 | 0 | [4,3,3] (10) |
[4,3]×[ ] (40) | [4]×[3] (80) |
[ ]×[3,3] (80) |
[3,3,3] (32) |
||||
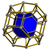
| 1 | (0,0,0,0,1)√2 | 5-orthoplex (Quadrirectified 5-cube) |
10 | 40 | 80 | 80 | 32 |  {3,3,4} 16-cell In four dimensional geometry, a 16-cell or hexadecachoron is a regular convex 4-polytope. It is one of the six regular convex 4-polytopes first described by the Swiss mathematician Ludwig Schläfli in the mid-19th century.... |
 {3,3,3} |
- | - | - | - |
| 2 | (0,0,0,1,1)√2 | Rectified 5-orthoplex (Trirectified 5-cube) |
42 | 200 | 400 | 320 | 80 |  { }×{3,4} Octahedral prism In geometry, a octahedral prism is a convex uniform polychoron . This polychoron has 10 polyhedral cells: 2 octahedra connected by 8 triangular prisms.- Related polytopes :... |
 {3,3,4} 16-cell In four dimensional geometry, a 16-cell or hexadecachoron is a regular convex 4-polytope. It is one of the six regular convex 4-polytopes first described by the Swiss mathematician Ludwig Schläfli in the mid-19th century.... |
- | - | - |  t1{3,3,3} Rectified 5-cell In four dimensional geometry, the rectified 5-cell is a uniform polychoron composed of 5 regular tetrahedral and 5 regular octahedral cells. Each edge has one tetrahedron and two octahedra. Each vertex has two tetrahedra and three octahedra. In total it has 30 triangle faces, 30 edges, and 10... |
| 3 | (0,0,0,1,2)√2 | Truncated 5-orthoplex Truncated 5-orthoplex In six-dimensional geometry, a truncated 5-orthoplex is a convex uniform 5-polytope, being a truncation of the regular 5-orthoplex.There are 4 unique truncations of the 5-orthoplex. Vertices of the truncation 5-orthoplex are located as pairs on the edge of the 5-orthoplex. Vertices of the... (Quadritruncated 5-cube) |
42 | 200 | 400 | 400 | 160 |  (Octah.pyr) |
 t0,1{3,3,3} Truncated 5-cell In geometry, a truncated 5-cell is a uniform polychoron formed as the truncation of the regular 5-cell.There are two degrees of trunctions, including a bitruncation.- Truncated 5-cell:... |
 {3,3,3} |
- | - | - |
| 4 | (0,0,1,1,1)√2 | Birectified 5-cube (Birectified 5-orthoplex) |
42 | 280 | 640 | 480 | 80 |  {4}×{3} Duoprism In geometry of 4 dimensions or higher, a duoprism is a polytope resulting from the Cartesian product of two polytopes, each of two dimensions or higher... |
 t1{3,3,4} |
- | - | - |  t1{3,3,3} Rectified 5-cell In four dimensional geometry, the rectified 5-cell is a uniform polychoron composed of 5 regular tetrahedral and 5 regular octahedral cells. Each edge has one tetrahedron and two octahedra. Each vertex has two tetrahedra and three octahedra. In total it has 30 triangle faces, 30 edges, and 10... |
| 5 | (0,0,1,1,2)√2 | Cantellated 5-orthoplex Cantellated 5-orthoplex In six-dimensional geometry, a cantellated 5-orthoplex is a convex uniform 5-polytope, being a cantellation of the regular 5-orthoplex.There are 6 cantellation for the 5-orthoplex, including truncations... (Tricantellated 5-cube) |
122 | 680 | 1520 | 1280 | 320 |  Prism-wedge |
t1{3,3,4} | { }×{3,4} | - | - |  t0,2{3,3,3} Cantellated 5-cell In four-dimensional geometry, a cantellated 5-cell is a convex uniform polychoron, being a cantellation of the regular 5-cell.There are 2 unique degrees of runcinations of the 5-cell including with permutations truncations.... |
| 6 | (0,0,1,2,2)√2 | Bitruncated 5-orthoplex (tritruncated 5-cube) |
42 | 280 | 720 | 800 | 320 |  |
t0,1{3,3,4} | - | - | - |  t1,2{3,3,3} |
| 7 | (0,0,1,2,3)√2 | Cantitruncated 5-orthoplex (tricantitruncated 5-orthoplex) |
122 | 680 | 1520 | 1600 | 640 | t0,2{3,3,4} | { }×t1{3,4} |  {6}×{4} Duoprism In geometry of 4 dimensions or higher, a duoprism is a polytope resulting from the Cartesian product of two polytopes, each of two dimensions or higher... |
- | 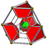 t0,1,3{3,3,3} |
|
| 8 | (0,1,1,1,1)√2 | Rectified 5-cube Rectified 5-cube In give-dimensional geometry, a rectified 5-cube is a convex uniform 5-polytope, being a rectification of the regular 5-cube.There are 5 degrees of rectifications of a 5-polytope, the zeroth here being the 5-cube, and the 4th and last being the 5-orthoplex. Vertices of the rectified 5-cube are... |
42 | 240 | 400 | 240 | 40 | 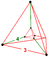 {3,3}x{ } |
 t1{4,3,3} Rectified tesseract In geometry, the rectified tesseract, or rectified 8-cell is a uniform polychoron bounded by 24 cells: 8 cuboctahedra, and 16 tetrahedra.... |
- | - | - |  {3,3,3} |
| 9 | (0,1,1,1,2)√2 | Runcinated 5-orthoplex Runcinated 5-orthoplex In six-dimensional geometry, a runcinated 5-orthoplex is a convex uniform 5-polytope with 3rd order truncation of the regular 5-orthoplex.There are 8 runcinations of the 5-orthoplex with permutations of truncations, and cantellations... |
202 | 1240 | 2160 | 1440 | 320 | 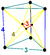 |
t1{4,3,3} | - |  {3}×{4} Duoprism In geometry of 4 dimensions or higher, a duoprism is a polytope resulting from the Cartesian product of two polytopes, each of two dimensions or higher... |
 t0,3{3,3,3} |
|
| 10 | (0,1,1,2,2)√2 | Bicantellated 5-cube (Bicantellated 5-orthoplex) |
122 | 840 | 2160 | 1920 | 480 | 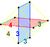 |
 t0,2{4,3,3} Cantellated tesseract In four-dimensional geometry, a cantellated tesseract is a convex uniform polychoron, being a cantellation of the regular tesseract.There are four degrees of cantellations of the tesseract including with permutations truncations... |
- |  {4}×{3} Duoprism In geometry of 4 dimensions or higher, a duoprism is a polytope resulting from the Cartesian product of two polytopes, each of two dimensions or higher... |
- |  t0,2{3,3,3} Cantellated 5-cell In four-dimensional geometry, a cantellated 5-cell is a convex uniform polychoron, being a cantellation of the regular 5-cell.There are 2 unique degrees of runcinations of the 5-cell including with permutations truncations.... |
| 11 | (0,1,1,2,3)√2 | Runcitruncated 5-orthoplex |
202 | 1560 | 3760 | 3360 | 960 | t0,2{3,3,4} | { }×t1{3,4} |  {6}×{4} Duoprism In geometry of 4 dimensions or higher, a duoprism is a polytope resulting from the Cartesian product of two polytopes, each of two dimensions or higher... |
- |  t0,1,3{3,3,3} |
|
| 12 | (0,1,2,2,2)√2 | Bitruncated 5-cube |
42 | 280 | 720 | 720 | 240 |  |
 t1,2{4,3,3} |
- | - | - |  t0,1{3,3,3} Truncated 5-cell In geometry, a truncated 5-cell is a uniform polychoron formed as the truncation of the regular 5-cell.There are two degrees of trunctions, including a bitruncation.- Truncated 5-cell:... |
| 13 | (0,1,2,2,3)√2 | Runcicantellated 5-orthoplex |
202 | 1240 | 2960 | 2880 | 960 | { }×t0,1{3,4} | t1,2{3,3,4} |  {3}×{4} Duoprism In geometry of 4 dimensions or higher, a duoprism is a polytope resulting from the Cartesian product of two polytopes, each of two dimensions or higher... |
- |  t0,1,3{3,3,3} |
|
| 14 | (0,1,2,3,3)√2 | Bicantitruncated 5-cube (Bicantitruncated 5-orthoplex) |
122 | 840 | 2160 | 2400 | 960 |  |
 t0,2{4,3,3} Cantellated tesseract In four-dimensional geometry, a cantellated tesseract is a convex uniform polychoron, being a cantellation of the regular tesseract.There are four degrees of cantellations of the tesseract including with permutations truncations... |
- |  {4}×{3} Duoprism In geometry of 4 dimensions or higher, a duoprism is a polytope resulting from the Cartesian product of two polytopes, each of two dimensions or higher... |
- |  t0,2{3,3,3} Cantellated 5-cell In four-dimensional geometry, a cantellated 5-cell is a convex uniform polychoron, being a cantellation of the regular 5-cell.There are 2 unique degrees of runcinations of the 5-cell including with permutations truncations.... |
| 15 | (0,1,2,3,4)√2 | Runcicantitruncated 5-orthoplex |
202 | 1560 | 4240 | 4800 | 1920 | t0,1,2{3,3,4} | { }×t0,1{3,4} |  {6}×{4} Duoprism In geometry of 4 dimensions or higher, a duoprism is a polytope resulting from the Cartesian product of two polytopes, each of two dimensions or higher... |
- |  t0,1,2,3{3,3,3} |
|
| 16 | (1,1,1,1,1) | 5-cube |
32 | 80 | 80 | 40 | 10 |  {3,3,3} |
 {4,3,3} Tesseract In geometry, the tesseract, also called an 8-cell or regular octachoron or cubic prism, is the four-dimensional analog of the cube. The tesseract is to the cube as the cube is to the square. Just as the surface of the cube consists of 6 square faces, the hypersurface of the tesseract consists of 8... |
- | - | - | - |
| 17 | (1,1,1,1,1) + (0,0,0,0,1)√2 |
Stericated 5-cube Stericated 5-cube In five-dimensional geometry, a stericated 5-cube is a convex uniform 5-polytope with fourth-order truncations of the regular 5-cube.... (Stericated 5-orthoplex) |
242 | 800 | 1040 | 640 | 160 |  Tetr.antiprm |
 {4,3,3} Tesseract In geometry, the tesseract, also called an 8-cell or regular octachoron or cubic prism, is the four-dimensional analog of the cube. The tesseract is to the cube as the cube is to the square. Just as the surface of the cube consists of 6 square faces, the hypersurface of the tesseract consists of 8... |
 {4,3}×{ } Tesseract In geometry, the tesseract, also called an 8-cell or regular octachoron or cubic prism, is the four-dimensional analog of the cube. The tesseract is to the cube as the cube is to the square. Just as the surface of the cube consists of 6 square faces, the hypersurface of the tesseract consists of 8... |
 {4}×{3} Duoprism In geometry of 4 dimensions or higher, a duoprism is a polytope resulting from the Cartesian product of two polytopes, each of two dimensions or higher... |
 { }×{3,3} |
 {3,3,3} |
| 18 | (1,1,1,1,1) + (0,0,0,1,1)√2 |
Runcinated 5-cube Runcinated 5-cube In five-dimensional geometry, a runcinated 5-cube is a convex uniform 5-polytope that is a runcination of the regular 5-cube.... |
162 | 1200 | 2160 | 1440 | 320 |  |
 t0,3{4,3,3} Runcinated tesseract In four-dimensional geometry, a runcinated tesseract is a convex uniform polychoron, being a runcination of the regular tesseract.... |
- |  {4}×{3} Duoprism In geometry of 4 dimensions or higher, a duoprism is a polytope resulting from the Cartesian product of two polytopes, each of two dimensions or higher... |
 { }×t1{3,3} |
 {3,3,3} |
| 19 | (1,1,1,1,1) + (0,0,0,1,2)√2 |
Steritruncated 5-orthoplex |
242 | 1600 | 2960 | 2240 | 640 | t0,3{3,3,4} | { }×{4,3} | - | - |  t0,1{3,3,3} Truncated 5-cell In geometry, a truncated 5-cell is a uniform polychoron formed as the truncation of the regular 5-cell.There are two degrees of trunctions, including a bitruncation.- Truncated 5-cell:... |
|
| 20 | (1,1,1,1,1) + (0,0,1,1,1)√2 |
Cantellated 5-cube Cantellated 5-cube In six-dimensional geometry, a cantellated 5-cube is a convex uniform 5-polytope, being a cantellation of the regular 5-cube.There are 6 unique cantellation for the 5-cube, including truncations... |
82 | 640 | 1520 | 1200 | 240 | 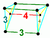 Prism-wedge |
 t0,2{4,3,3} Cantellated tesseract In four-dimensional geometry, a cantellated tesseract is a convex uniform polychoron, being a cantellation of the regular tesseract.There are four degrees of cantellations of the tesseract including with permutations truncations... |
- | - |  { }×{3,3} |
 t1{3,3,3} Rectified 5-cell In four dimensional geometry, the rectified 5-cell is a uniform polychoron composed of 5 regular tetrahedral and 5 regular octahedral cells. Each edge has one tetrahedron and two octahedra. Each vertex has two tetrahedra and three octahedra. In total it has 30 triangle faces, 30 edges, and 10... |
| 21 | (1,1,1,1,1) + (0,0,1,1,2)√2 |
Stericantellated 5-cube (Stericantellated 5-orthoplex) |
242 | 2080 | 4720 | 3840 | 960 |  t0,2{4,3,3} Cantellated tesseract In four-dimensional geometry, a cantellated tesseract is a convex uniform polychoron, being a cantellation of the regular tesseract.There are four degrees of cantellations of the tesseract including with permutations truncations... |
 t0,2{4,3}×{ } Cantellated tesseract In four-dimensional geometry, a cantellated tesseract is a convex uniform polychoron, being a cantellation of the regular tesseract.There are four degrees of cantellations of the tesseract including with permutations truncations... |
 {4}×{3} Duoprism In geometry of 4 dimensions or higher, a duoprism is a polytope resulting from the Cartesian product of two polytopes, each of two dimensions or higher... |
 { }×t0,2{3,3} |
 t0,2{3,3,3} Cantellated 5-cell In four-dimensional geometry, a cantellated 5-cell is a convex uniform polychoron, being a cantellation of the regular 5-cell.There are 2 unique degrees of runcinations of the 5-cell including with permutations truncations.... |
|
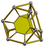
| 22 | (1,1,1,1,1) + (0,0,1,2,2)√2 |
Runcicantellated 5-cube |
162 | 1200 | 2960 | 2880 | 960 |  t0,1,3{4,3,3} |
- |  {4}×{3} Duoprism In geometry of 4 dimensions or higher, a duoprism is a polytope resulting from the Cartesian product of two polytopes, each of two dimensions or higher... |
 { }×t0,1{3,3} Truncated tetrahedral prism In geometry, a truncated tetrahedral prism is a convex uniform polychoron . This polychoron has 10 polyhedral cells: 2 truncated tetrahedra connected by 4 triangular prisms and 4 hexagonal prisms. It has 24 faces: 8 triangular, 18 square, and 8 hexagons. It has 48 edges and 24 vertices.Alternative... |
 t1,2{3,3,3} |
|
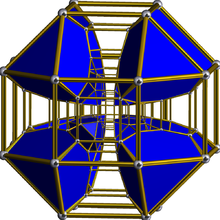
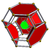
| 23 | (1,1,1,1,1) + (0,0,1,2,3)√2 |
Stericantitruncated 5-orthoplex |
242 | 2400 | 6000 | 5760 | 1920 |  { }×t0,2{3,4} Rhombicuboctahedral prism In geometry, a rhombicuboctahedral prism is a convex uniform polychoron .It is one of 18 convex uniform polyhedral prisms created by using uniform prisms to connect pairs of Platonic solids or Archimedean solids in parallel hyperplanes.- Alternative names :* rhombicuboctahedral dyadic prism In... |
 t0,1,3{3,3,4} |
 {6}×{4} Duoprism In geometry of 4 dimensions or higher, a duoprism is a polytope resulting from the Cartesian product of two polytopes, each of two dimensions or higher... |
 { }×t0,1{3,3} Truncated tetrahedral prism In geometry, a truncated tetrahedral prism is a convex uniform polychoron . This polychoron has 10 polyhedral cells: 2 truncated tetrahedra connected by 4 triangular prisms and 4 hexagonal prisms. It has 24 faces: 8 triangular, 18 square, and 8 hexagons. It has 48 edges and 24 vertices.Alternative... |
 t0,1,2{3,3,3} |
|
| 24 | (1,1,1,1,1) + (0,1,1,1,1)√2 |
Truncated 5-cube Truncated 5-cube In five-dimensional geometry, a truncated 5-cube is a convex uniform 5-polytope, being a truncation of the regular 5-cube.There are four unique truncations of the 5-cube. Vertices of the truncated 5-cube are located as pairs on the edge of the 5-cube. Vertices of the bitruncated 5-cube are located... |
42 | 240 | 400 | 280 | 80 |  Tetrah.pyr |
 t0,1{4,3,3} Truncated tesseract In geometry, a truncated tesseract is a uniform polychoron formed as the truncation of the regular tesseract.There are three trunctions, including a bitruncation, and a tritruncation, which creates the truncated 16-cell.... |
- | - | - |  {3,3,3} |
| 25 | (1,1,1,1,1) + (0,1,1,1,2)√2 |
Steritruncated 5-cube |
242 | 1520 | 2880 | 2240 | 640 |  t0,1{4,3,3} Truncated tesseract In geometry, a truncated tesseract is a uniform polychoron formed as the truncation of the regular tesseract.There are three trunctions, including a bitruncation, and a tritruncation, which creates the truncated 16-cell.... |
 t0,1{4,3}×{ } Truncated cubic prism In geometry, a truncated cubic prism is a convex uniform polychoron .It is one of 18 convex uniform polyhedral prisms created by using uniform prisms to connect pairs of Platonic solids or Archimedean solids in parallel hyperplanes.- Alternative names :* Truncated-cubic hyperprism* Truncated-cubic... |
{8}×{3} Duoprism In geometry of 4 dimensions or higher, a duoprism is a polytope resulting from the Cartesian product of two polytopes, each of two dimensions or higher... |
 { }×{3,3} |
 t0,3{3,3,3} |
|
| 26 | (1,1,1,1,1) + (0,1,1,2,2)√2 |
Runcitruncated 5-cube |
162 | 1440 | 3680 | 3360 | 960 |  t0,1,3{4,3,3} |
{ }×t0,1{4,3} | {6}×{8} Duoprism In geometry of 4 dimensions or higher, a duoprism is a polytope resulting from the Cartesian product of two polytopes, each of two dimensions or higher... |
{ }×t0,1{3,3} | t0,1,3{3,3,3}]] | |
| 27 | (1,1,1,1,1) + (0,1,1,2,3)√2 |
Steriruncitruncated 5-cube (Steriruncitruncated 5-orthoplex) |
242 | 2160 | 5760 | 5760 | 1920 |  t0,1,3{4,3,3} |
 t0,1{4,3}×{ } Truncated cubic prism In geometry, a truncated cubic prism is a convex uniform polychoron .It is one of 18 convex uniform polyhedral prisms created by using uniform prisms to connect pairs of Platonic solids or Archimedean solids in parallel hyperplanes.- Alternative names :* Truncated-cubic hyperprism* Truncated-cubic... |
{8}×{6} Duoprism In geometry of 4 dimensions or higher, a duoprism is a polytope resulting from the Cartesian product of two polytopes, each of two dimensions or higher... |
 { }×t0,1{3,3} Truncated tetrahedral prism In geometry, a truncated tetrahedral prism is a convex uniform polychoron . This polychoron has 10 polyhedral cells: 2 truncated tetrahedra connected by 4 triangular prisms and 4 hexagonal prisms. It has 24 faces: 8 triangular, 18 square, and 8 hexagons. It has 48 edges and 24 vertices.Alternative... |
 t0,1,3{3,3,3} |
|
| 28 | (1,1,1,1,1) + (0,1,2,2,2)√2 |
cantitruncated 5-cube |
82 | 640 | 1520 | 1440 | 480 |  t0,1,2{4,3,3} |
- | - |  { }×{3,3} |
 t0,1{3,3,3} Truncated 5-cell In geometry, a truncated 5-cell is a uniform polychoron formed as the truncation of the regular 5-cell.There are two degrees of trunctions, including a bitruncation.- Truncated 5-cell:... |
|
| 29 | (1,1,1,1,1) + (0,1,2,2,3)√2 |
Stericantitruncated 5-cube |
242 | 2320 | 5920 | 5760 | 1920 |  t0,1,2{4,3,3} |
 t0,1,2{4,3}×{ } Truncated cuboctahedral prism In geometry, a truncated cuboctahedral prism is a convex uniform polychoron .It is one of 18 convex uniform polyhedral prisms created by using uniform prisms to connect pairs of Platonic solids or Archimedean solids in parallel hyperplanes.- Alternative names :* Truncated-cuboctahedral dyadic prism... |
{8}×{3} Duoprism In geometry of 4 dimensions or higher, a duoprism is a polytope resulting from the Cartesian product of two polytopes, each of two dimensions or higher... |
 { }×t0,2{3,3} |
 t0,1,3{3,3,3} |
|
| 30 | (1,1,1,1,1) + (0,1,2,3,3)√2 |
Runcicantitruncated 5-cube |
162 | 1440 | 4160 | 4800 | 1920 |  t0,1,2,3{4,3,3} |
- | {8}×{3} Duoprism In geometry of 4 dimensions or higher, a duoprism is a polytope resulting from the Cartesian product of two polytopes, each of two dimensions or higher... |
 { }×t0,1{3,3} Truncated tetrahedral prism In geometry, a truncated tetrahedral prism is a convex uniform polychoron . This polychoron has 10 polyhedral cells: 2 truncated tetrahedra connected by 4 triangular prisms and 4 hexagonal prisms. It has 24 faces: 8 triangular, 18 square, and 8 hexagons. It has 48 edges and 24 vertices.Alternative... |
 t0,1,2{3,3,3} |
|
| 31 | (1,1,1,1,1) + (0,1,2,3,4)√2 |
Omnitruncated 5-cube (omnitruncated 5-orthoplex) |
242 | 2640 | 8160 | 9600 | 3840 |  Irr. {3,3,3} |
 t0,1,2{4,3}×{ } Truncated cuboctahedral prism In geometry, a truncated cuboctahedral prism is a convex uniform polychoron .It is one of 18 convex uniform polyhedral prisms created by using uniform prisms to connect pairs of Platonic solids or Archimedean solids in parallel hyperplanes.- Alternative names :* Truncated-cuboctahedral dyadic prism... |
 t0,1,2{4,3}×{ } Truncated cuboctahedral prism In geometry, a truncated cuboctahedral prism is a convex uniform polychoron .It is one of 18 convex uniform polyhedral prisms created by using uniform prisms to connect pairs of Platonic solids or Archimedean solids in parallel hyperplanes.- Alternative names :* Truncated-cuboctahedral dyadic prism... |
{8}×{6} Duoprism In geometry of 4 dimensions or higher, a duoprism is a polytope resulting from the Cartesian product of two polytopes, each of two dimensions or higher... |
 { }×t0,1,2{3,3} |
 t0,1,2,3{3,3,3} |
The D5 family
The D5 family has symmetry of order 1920 (5! x 24).This family has 23 Wythoffian uniform polyhedra, from 3x8-1 permutations of the D5 Coxeter-Dynkin diagram
Coxeter-Dynkin diagram
In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors...
with one or more rings. 15 (2x8-1) are repeated from the B5 family and 8 are unique to this family.
See symmetry graphs: List of D5 polytopes
| # | Coxeter-Dynkin diagram Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... Schläfli symbol symbols Johnson and Bowers names |
Element counts | Vertex figure Vertex figure In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:... |
Facets by location: 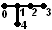 [31,2,1] [31,2,1] |
||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 4 | 3 | 2 | 1 | 0 | [3,3,3] (16) |
[31,1,1] (10) |
[3,3]×[ ] (40) |
[ ]×[3]×[ ] (80) |
[3,3,3] (16) |
|||
| 51 | (121) 5-demicube Hemipenteract (hin) |
26 | 120 | 160 | 80 | 16 |  t1{3,3,3} Rectified 5-cell In four dimensional geometry, the rectified 5-cell is a uniform polychoron composed of 5 regular tetrahedral and 5 regular octahedral cells. Each edge has one tetrahedron and two octahedra. Each vertex has two tetrahedra and three octahedra. In total it has 30 triangle faces, 30 edges, and 10... |
{3,3,3} | t0(111) | - | - | - |
| 52 | t0,1(121) Truncated 5-demicube Truncated hemipenteract (thin) |
42 | 280 | 640 | 560 | 160 | ||||||
| 53 | t0,2(121) Cantellated 5-demicube Cantellated 5-demicube In six-dimensional geometry, a cantellated 5-demicube is a convex uniform 5-polytope, being a cantellation of the uniform 5-demicube.There are 2 unique cantellation for the 5-demicube including a truncation.- Cantellated 5-demicube:... Small rhombated hemipenteract (sirhin) |
42 | 360 | 880 | 720 | 160 | ||||||
| 54 | t0,3(121) Runcinated 5-demicube Runcinated 5-demicube In five-dimensional geometry, a runcinated 5-demicube is a convex uniform 5-polytope with a runcination operation, a 3rd order truncations the uniform 5-demicube.... Small prismated hemipenteract (siphin) |
82 | 480 | 720 | 400 | 80 | ||||||
| 55 | t0,1,2(121) Cantitruncated 5-demicube Great rhombated hemipenteract (girhin) |
42 | 360 | 1040 | 1200 | 480 | ||||||
| 56 | t0,1,3(121) Runcitruncated 5-demicube Prismatotruncated hemipenteract (pithin) |
82 | 720 | 1840 | 1680 | 480 | ||||||
| 57 | t0,2,3(121) Runcicantellated 5-demicube Prismatorhombated hemipenteract (pirhin) |
82 | 560 | 1280 | 1120 | 320 | ||||||
| 58 | t0,1,2,3(121) Runcicantitruncated 5-demicube Great prismated hemipenteract (giphin) |
82 | 720 | 2080 | 2400 | 960 |
Uniform prismatic forms
There are 5 finite categorical uniformUniform polytope
A uniform polytope is a vertex-transitive polytope made from uniform polytope facets of a lower dimension. Uniform polytopes of 2 dimensions are the regular polygons....
prismatic families of polytopes based on the nonprismatic uniform 4-polytopes:
A4 × A1
This prismatic family has 9 forms:The A1 x A4 family has symmetry of order 240 (2*5!).
| # | Coxeter-Dynkin Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... and Schläfli symbols Name |
Element counts | ||||
|---|---|---|---|---|---|---|
| Facets | Cells | Faces | Edges | Vertices | ||
| 59 | {3,3,3}x{ } 5-cell prism |
7 | 20 | 30 | 25 | 10 |
| 60 | t1{3,3,3}x{ } Rectified 5-cell prism |
12 | 50 | 90 | 70 | 20 |
| 61 | t0,1{3,3,3}x{ } Truncated 5-cell prism |
12 | 50 | 100 | 100 | 40 |
| 62 | t0,2{3,3,3}x{ } Cantellated 5-cell prism |
22 | 120 | 250 | 210 | 60 |
| 63 | t0,3{3,3,3}x{ } Runcinated 5-cell prism |
32 | 130 | 200 | 140 | 40 |
| 64 | t1,2{3,3,3}x{ } Bitruncated 5-cell prism |
12 | 60 | 140 | 150 | 60 |
| 65 | t0,1,2{3,3,3}x{ } Cantitruncated 5-cell prism |
22 | 120 | 280 | 300 | 120 |
| 66 | t0,1,3{3,3,3}x{ } Runcitruncated 5-cell prism |
32 | 180 | 390 | 360 | 120 |
| 67 | t0,1,2,3{3,3,3}x{ } Omnitruncated 5-cell prism |
32 | 210 | 540 | 600 | 240 |
B4 × A1
This prismatic family has 16 forms. (Three are shared with [3,4,3]×[ ] family)The A1 x B4 family has symmetry of order 768 (2*2^4*4!).
| # | Coxeter-Dynkin Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... and Schläfli symbols Name |
Element counts | ||||
|---|---|---|---|---|---|---|
| Facets | Cells | Faces | Edges | Vertices | ||
| 68 | {4,3,3}x{ } Tesseractic prism |
10 | 40 | 80 | 80 | 32 |
| 69 | t1{4,3,3}x{ } Rectified tesseractic prism |
26 | 136 | 272 | 224 | 64 |
| 70 | t0,1{4,3,3}x{ } Truncated tesseractic prism |
26 | 136 | 304 | 320 | 128 |
| 71 | t0,2{4,3,3}x{ } Cantellated tesseractic prism |
58 | 360 | 784 | 672 | 192 |
| 72 | t0,3{4,3,3}x{ } Runcinated tesseractic prism |
82 | 368 | 608 | 448 | 128 |
| 73 | t1,2{4,3,3}x{ } Bitruncated tesseractic prism |
26 | 168 | 432 | 480 | 192 |
| 74 | t0,1,2{4,3,3}x{ } Cantitruncated tesseractic prism |
58 | 360 | 880 | 960 | 384 |
| 75 | t0,1,3{4,3,3}x{ } Runcitruncated tesseractic prism |
82 | 528 | 1216 | 1152 | 384 |
| 76 | t0,1,2,3{4,3,3}x{ } Omnitruncated tesseractic prism |
82 | 624 | 1696 | 1920 | 768 |
| 77 | {3,3,4}x{ } 16-cell prism |
18 | 64 | 88 | 56 | 16 |
| 78 | t1{3,3,4}x{ } Rectified 16-cell prism (Same as 24-cell prism) |
26 | 144 | 288 | 216 | 48 |
| 79 | t0,1{3,3,4}x{ } Truncated 16-cell prism |
26 | 144 | 312 | 288 | 96 |
| 80 | t0,2{3,3,4}x{ } Cantellated 16-cell prism (Same as rectified 24-cell prism) |
50 | 336 | 768 | 672 | 192 |
| 81 | t0,1,2{3,3,4}x{ } Cantitruncated 16-cell prism (Same as truncated 24-cell prism) |
50 | 336 | 864 | 960 | 384 |
| 82 | t0,1,3{3,3,4}x{ } Runcitruncated 16-cell prism |
82 | 528 | 1216 | 1152 | 384 |
F4 × A1
This prismatic family has 10 forms.The A1 x F4 family has symmetry of order 2304 (2*1152).
| # | Coxeter-Dynkin Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... and Schläfli symbols Name |
Element counts | ||||
|---|---|---|---|---|---|---|
| Facets | Cells | Faces | Edges | Vertices | ||
| [79] | {3,4,3}x{ } 24-cell prism |
26 | 144 | 288 | 216 | 48 |
| [80] | t1{3,4,3}x{ } rectified 24-cell prism |
50 | 336 | 768 | 672 | 192 |
| [81] | t0,1{3,4,3}x{ } truncated 24-cell prism |
50 | 336 | 864 | 960 | 384 |
| 84 | t0,2{3,4,3}x{ } cantellated 24-cell prism |
146 | 1008 | 2304 | 2016 | 576 |
| 85 | t0,3{3,4,3}x{ } runcinated 24-cell prism |
242 | 1152 | 1920 | 1296 | 288 |
| 86 | t1,2{3,4,3}x{ } bitruncated 24-cell prism |
50 | 432 | 1248 | 1440 | 576 |
| 87 | t0,1,2{3,4,3}x{ } cantitruncated 24-cell prism |
146 | 1008 | 2592 | 2880 | 1152 |
| 88 | t0,1,3{3,4,3}x{ } runcitruncated 24-cell prism |
242 | 1584 | 3648 | 3456 | 1152 |
| 89 | t0,1,2,3{3,4,3}x{ } omnitruncated 24-cell prism |
242 | 1872 | 5088 | 5760 | 2304 |
| [83] | h0,1{3,4,3}x{ } snub 24-cell prism |
146 | 768 | 1392 | 960 | 192 |
H4 × A1
This prismatic family has 15 forms:The A1 x H4 family has symmetry of order 28800 (2*14400).
| # | Coxeter-Dynkin Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... and Schläfli symbols Name |
Element counts | ||||
|---|---|---|---|---|---|---|
| Facets | Cells | Faces | Edges | Vertices | ||
| 90 | {5,3,3}x{ } 120-cell prism |
122 | 960 | 2640 | 3000 | 1200 |
| 91 | t1{5,3,3}x{ } Rectified 120-cell prism |
722 | 4560 | 9840 | 8400 | 2400 |
| 92 | t0,1{5,3,3}x{ } Truncated 120-cell prism |
722 | 4560 | 11040 | 12000 | 4800 |
| 93 | t0,2{5,3,3}x{ } Cantellated 120-cell prism |
1922 | 12960 | 29040 | 25200 | 7200 |
| 94 | t0,3{5,3,3}x{ } Runcinated 120-cell prism |
2642 | 12720 | 22080 | 16800 | 4800 |
| 95 | t1,2{5,3,3}x{ } Bitruncated 120-cell prism |
722 | 5760 | 15840 | 18000 | 7200 |
| 96 | t0,1,2{5,3,3}x{ } Cantitruncated 120-cell prism |
1922 | 12960 | 32640 | 36000 | 14400 |
| 97 | t0,1,3{5,3,3}x{ } Runcitruncated 120-cell prism |
2642 | 18720 | 44880 | 43200 | 14400 |
| 98 | t0,1,2,3{5,3,3}x{ } Omnitruncated 120-cell prism |
2642 | 22320 | 62880 | 72000 | 28800 |
| 99 | {3,3,5}x{ } 600-cell prism |
602 | 2400 | 3120 | 1560 | 240 |
| 100 | t1{3,3,5}x{ } Rectified 600-cell prism |
722 | 5040 | 10800 | 7920 | 1440 |
| 101 | t0,1{3,3,5}x{ } Truncated 600-cell prism |
722 | 5040 | 11520 | 10080 | 2880 |
| 102 | t0,2{3,3,5}x{ } Cantellated 600-cell prism |
1442 | 11520 | 28080 | 25200 | 7200 |
| 103 | t0,1,2{3,3,5}x{ } Cantitruncated 600-cell prism |
1442 | 11520 | 31680 | 36000 | 14400 |
| 104 | t0,1,3{3,3,5}x{ } Runcitruncated 600-cell prism |
2642 | 18720 | 44880 | 43200 | 14400 |
Grand antiprism prism
The grand antiprism prism is the only known convex nonwythoffian uniform polyteron. It has 200 vertices, 1100 edges, 1940 faces (40 pentagons, 500 squares, 1400 triangles), 1360 cells (300 tetrahedronTetrahedron
In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...
s, 20 pentagonal antiprism
Pentagonal antiprism
In geometry, the pentagonal antiprism is the third in an infinite set of antiprisms formed by an even-numbered sequence of triangle sides closed by two polygon caps. It consists of two pentagons joined to each other by a ring of 10 triangles for a total of 12 faces...
s, 700 triangular prism
Triangular prism
In geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides....
s, 20 pentagonal prism
Pentagonal prism
In geometry, the pentagonal prism is a prism with a pentagonal base. It is a type of heptahedron with 7 faces, 15 edges, and 10 vertices.- As a semiregular polyhedron :...
s), 322 hypercells (2 grand antiprism
Grand antiprism
In geometry, the grand antiprism or pentagonal double antiprismoid is a uniform polychoron bounded by 320 cells: 20 pentagonal antiprisms, and 300 tetrahedra. It is an anomalous, non-Wythoffian uniform polychoron, discovered in 1965 by Conway and Guy.- Alternate names :* Pentagonal double...
s
 , 20 pentagonal antiprism
, 20 pentagonal antiprismPentagonal antiprism
In geometry, the pentagonal antiprism is the third in an infinite set of antiprisms formed by an even-numbered sequence of triangle sides closed by two polygon caps. It consists of two pentagons joined to each other by a ring of 10 triangles for a total of 12 faces...
prisms
 , and 300 tetrahedral prisms
, and 300 tetrahedral prisms  ).
).| # | Name | Element counts | ||||
|---|---|---|---|---|---|---|
| Facets | Cells | Faces | Edges | Vertices | ||
| 105 | grand antiprism prism Gappip |
322 | 1360 | 1940 | 1100 | 200 |
Regular and uniform honeycombs
There are five fundamental affine Coxeter groups, and 13 prismatic groups that generate regular and uniform tessellations in Euclidean 4-space.| # | Coxeter group Coxeter group In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example... |
Coxeter-Dynkin diagram Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... |
||
|---|---|---|---|---|
| 1 |  |
[3[5]] | [(3,3,3,3,3)] | |
| 2 | 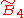 |
[4,3,31,1] | ||
| 3 | 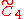 |
[4,3,3,4] | h[4,3,3,4] | |
| 4 | 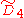 |
[31,1,1,1] | q[4,3,3,4] | |
| 5 | 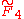 |
[3,4,3,3] | ||
| # | Coxeter group Coxeter group In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example... |
Coxeter-Dynkin diagram Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... |
|
|---|---|---|---|
| 1 | 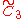 x x |
[4,3,4]x[∞] | |
| 2 | 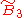 x x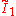 |
[4,31,1]x[∞] | |
| 3 | 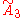 x x |
[3[4]]x[∞] | |
| 4 |  x x x x |
[4,4]x[∞]x[∞] | |
| 5 | 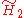 x x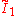 x x |
[6,3]x[∞]x[∞] | |
| 6 | 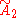 x x x x |
[3[3]]x[∞]x[∞] | |
| 7 | 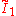 x x x x x x |
[∞]x[∞]x[∞]x[∞] | |
| 8 |  x x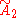 |
[3[3]]x[3[3]] | |
| 9 | 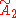 x x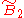 |
[3[3]]x[4,4] | |
| 10 | 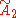 x x |
[3[3]]x[6,3] | |
| 11 |  x x |
[4,4]x[4,4] | |
| 12 |  x x |
[4,4]x[6,3] | |
| 13 | 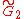 x x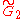 |
[6,3]x[6,3] | |
There are three regular honeycombs of Euclidean 4-space:
- tesseractic honeycomb, with symbols {4,3,3,4}, = . There are 19 uniform honeycombs in this family.
- 24-cell honeycomb, with symbols {3,4,3,3}, . There are 31 reflective uniform honeycombs in this family, and one alternated form.
- Snub 24-cell honeycombSnub 24-cell honeycombIn four-dimensional Euclidean geometry, the snub 24-cell honeycomb, or snub icositetrachoric honeycomb is a uniform space-filling tessellation by snub 24-cells, 16-cells, and 5-cells. It was discovered by Thorold Gosset with his 1900 paper of semiregular polytopes...
, with symbols h0,1{3,4,3,3}, constructed by four snub 24-cellSnub 24-cellIn geometry, the snub 24-cell is a convex uniform polychoron composed of 120 regular tetrahedral and 24 icosahedral cells. Five tetrahedra and three icosahedra meet at each vertex. In total it has 480 triangular faces, 432 edges, and 96 vertices....
, one 16-cell16-cellIn four dimensional geometry, a 16-cell or hexadecachoron is a regular convex 4-polytope. It is one of the six regular convex 4-polytopes first described by the Swiss mathematician Ludwig Schläfli in the mid-19th century....
, and five 5-cells at each vertex.
- Snub 24-cell honeycomb
- 4-demicube honeycomb, with symbols {3,3,4,3},
Other families that generate uniform honeycombs:
- There are 23 uniform honeycombs, 4 unique in the demitesseractic honeycomb family. With symbols h{4,32,4} it is geometrically identical to the hexadecachoric honeycomb, =
- There are 7 uniform honeycombs from the
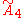 , family, all unique, including:
, family, all unique, including:
- 4-simplex honeycomb
- Truncated 4-simplex honeycombTruncated 4-simplex honeycombIn four-dimensional Euclidean geometry, the truncated 4-simplex honeycomb, truncated 5-cell honeycomb is a space-filling tessellation honeycomb...
- Omnitruncated 4-simplex honeycombOmnitruncated 4-simplex honeycombIn four-dimensional Euclidean geometry, the omnitruncated 4-simplex honeycomb or omnitruncated 5-cell honeycomb is a space-filling tessellation honeycomb. It is composed entirely of omnitruncated 5-cell facets....
- There are 9 uniform honeycombs in the
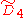 : [31,1,1,1] family, all repeated in other families, including the demitesseractic honeycomb.
: [31,1,1,1] family, all repeated in other families, including the demitesseractic honeycomb.
Non-Wythoffian uniform tessellations in 4-space also exist by elongation (inserting layers), and gyration (rotating layers) from these reflective forms.
Regular tessellations of hyperbolic 4-space
There are five kinds of convex regular honeycombsHoneycomb (geometry)
In geometry, a honeycomb is a space filling or close packing of polyhedral or higher-dimensional cells, so that there are no gaps. It is an example of the more general mathematical tiling or tessellation in any number of dimensions....
and four kinds of star-honeycombs in H4 space:
| Honeycomb name | Schläfli Symbol {p,q,r,s} |
Coxeter-Dynkin diagram Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... |
Facet type {p,q,r} |
Cell type {p,q} |
Face type {p} |
Face figure {s} |
Edge figure {r,s} |
Vertex figure Vertex figure In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:... {q,r,s} |
Dual Dual polyhedron In geometry, polyhedra are associated into pairs called duals, where the vertices of one correspond to the faces of the other. The dual of the dual is the original polyhedron. The dual of a polyhedron with equivalent vertices is one with equivalent faces, and of one with equivalent edges is another... |
|---|---|---|---|---|---|---|---|---|---|
| Order-5 pentachoric | {3,3,3,5} | {3,3,3} | {3,3} | {3} | {5} | {3,5} | {3,3,5} | {5,3,3,3} | |
| Order-3 hecatonicosachoric | {5,3,3,3} | {5,3,3} | {5,3} | {5} | {3} | {3,3} | {3,3,3} | {3,3,3,5} | |
| Order-5 tesseractic | {4,3,3,5} | {4,3,3} | {4,3} | {4} | {5} | {3,5} | {3,3,5} | {5,3,3,4} | |
| Order-4 hecatonicosachoric | {5,3,3,4} | {5,3,3} | {5,3} | {5} | {4} | {3,4} | {3,3,4} | {4,3,3,5} | |
| Order-5 hecatonicosachoric | {5,3,3,5} | {5,3,3} | {5,3} | {5} | {5} | {3,5} | {3,3,5} | Self-dual |
There are four regular star-honeycombs in H4 space:
| Honeycomb name | Schläfli Symbol {p,q,r,s} |
Coxeter-Dynkin diagram Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... |
Facet type {p,q,r} |
Cell type {p,q} |
Face type {p} |
Face figure {s} |
Edge figure {r,s} |
Vertex figure Vertex figure In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:... {q,r,s} |
Dual Dual polyhedron In geometry, polyhedra are associated into pairs called duals, where the vertices of one correspond to the faces of the other. The dual of the dual is the original polyhedron. The dual of a polyhedron with equivalent vertices is one with equivalent faces, and of one with equivalent edges is another... |
|---|---|---|---|---|---|---|---|---|---|
| Order-3 stellated hecatonicosachoric | {5/2,5,3,3} | {5/2,5,3} | {5/2,5} | {5} | {5} | {3,3} | {5,3,3} | {3,3,5,5/2} | |
| Order-5/2 hexacosichoric | {3,3,5,5/2} | {3,3,5} | {3,3} | {3} | {5/2} | {5,5/2} | {3,5,5/2} | {5/2,5,3,3} | |
| Order-5 icosahedral hecatonicosachoric | {3,5,5/2,5} | {3,5,5/2} | {3,5} | {3} | {5} | {5/2,5} | {5,5/2,5} | {5,5/2,5,3} | |
| Order-3 great hecatonicosachoric | {5,5/2,5,3} | {5,5/2,5} | {5,5/2} | {5} | {3} | {5,3} | {5/2,5,3} | {3,5,5/2,5} |
Regular and uniform hyperbolic honeycombs
There are 5 compact hyperbolic Coxeter groups of rank 5, each generating uniform honeycombs in hyperbolic 4-space as permutations of rings of the Coxeter diagrams. There are also 9 noncompact hyperbolic Coxeter groups of rank 5, each generating uniform honeycombs in 4-space as permutations of rings of the Coxeter diagrams. Noncompact groups generate honeycombs with inifinite facets or vertex figures. = [(3,3,3,3,4)]: = [(3,3,3,3,4)]: |
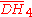 = [5,3,31,1]: = [5,3,31,1]: |
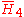 = [3,3,3,5]: = [3,3,3,5]:  = [4,3,3,5]: = [4,3,3,5]: 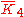 = [5,3,3,5]: = [5,3,3,5]: |
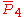 = [3,3[4]]: = [3,3[4]]:
|
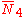 = [4,/3\,3,4]: = [4,/3\,3,4]:  = [3,4,31,1]: = [3,4,31,1]: 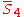 = [4,32,1]: = [4,32,1]: 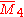 = [4,31,1,1]: = [4,31,1,1]: |
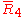 = [3,4,3,4]: = [3,4,3,4]: |
External links
- Polytope names, Guy Inchbald
- Polytopes of Various Dimensions, Jonathan Bowers
- Glossary for hyperspace: Polytope, George OlshevskyGeorge OlshevskyGeorge Olshevsky is a freelance editor, writer, publisher, amateur paleontologist, and mathematician living in San Diego, California.Olshevsky maintains the comprehensive online Dinosaur Genera List...
- Multi-dimensional Glossary, Garrett Jones
- polytope names, Wendy Krieger


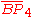 = [4,3[4]]:
= [4,3[4]]: 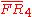 = [(3,3,4,3,4)]:
= [(3,3,4,3,4)]: 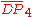 = [3[3]x[ ]]:
= [3[3]x[ ]]: