
Cantellated 5-cube
Encyclopedia
5-cube |
Cantellated 5-cube |
Bicantellated 5-cube |
Cantellated 5-orthoplex Cantellated 5-orthoplex In six-dimensional geometry, a cantellated 5-orthoplex is a convex uniform 5-polytope, being a cantellation of the regular 5-orthoplex.There are 6 cantellation for the 5-orthoplex, including truncations... |
5-orthoplex |
Cantitruncated 5-cube |
Bicantitruncated 5-cube |
Cantitruncated 5-orthoplex |
| Orthogonal projections in BC5 Coxeter plane | |||
|---|---|---|---|
In six-dimensional geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, a cantellated 5-cube is a convex uniform 5-polytope, being a cantellation of the regular 5-cube.
There are 6 unique cantellation for the 5-cube, including truncations. Half of them are more easily constructed from the dual 5-orthoplex
Cantellated 5-cube
| Cantellated 5-cube | ||
| Type | Uniform 5-polytope | |
| Schläfli symbol | t0,2{4,3,3,3} | |
| Coxeter-Dynkin diagram Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... |
colspan=2| | |
| 4-faces | 82 | |
| Cells | 640 | |
| Faces | 1520 | |
| Edges | 1200 | |
| Vertices | 240 | |
| Vertex figure Vertex figure In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:... |
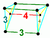 |
|
| Coxeter group Coxeter group In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example... |
BC5 [4,3,3,3] | |
| Properties | convex Convex polytope A convex polytope is a special case of a polytope, having the additional property that it is also a convex set of points in the n-dimensional space Rn... |
|
Coordinates
The Cartesian coordinates of the vertices of a cantellated 5-cube having edge length 2 are all permutations of: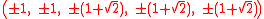
Bicantellated 5-cube
| Bicantellated 5-cube | ||
| Type | Uniform 5-polytope | |
| Schläfli symbol | t1,3{4,3,3,3} | |
| Coxeter-Dynkin diagram Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... |
colspan=2| |
|
| 4-faces | 122 | |
| Cells | 840 | |
| Faces | 2160 | |
| Edges | 1920 | |
| Vertices | 480 | |
| Vertex figure Vertex figure In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:... |
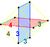 |
|
| Coxeter group Coxeter group In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example... |
BC5 [4,3,3,3] | |
| Properties | convex Convex polytope A convex polytope is a special case of a polytope, having the additional property that it is also a convex set of points in the n-dimensional space Rn... |
|
In five-dimensional geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, a bicantellated 5-cube is a uniform 5-polytope.
Alternate names
- Bicantellated penteract, bicantellated 5-orthoplex, or bicantellated pentacross
- Small birhombated penteractitriacontiditeron (Acronym: sibrant) (Jonathan Bowers)
Coordinates
The Cartesian coordinates of the vertices of a bicantellated 5-cube having edge length 2 are all permutations of:Cantitruncated 5-cube
| Cantitruncated 5-cube | ||
| Type | Uniform 5-polytope | |
| Schläfli symbol | t0,1,2{4,3,3,3} | |
| Coxeter-Dynkin diagram Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... |
||
| 4-faces | 82 | |
| Cells | 640 | |
| Faces | 1520 | |
| Edges | 1440 | |
| Vertices | 480 | |
| Vertex figure Vertex figure In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:... |
||
| Coxeter group Coxeter group In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example... |
BC5 [4,3,3,3] | |
| Properties | convex Convex polytope A convex polytope is a special case of a polytope, having the additional property that it is also a convex set of points in the n-dimensional space Rn... , isogonal Isogonal Isogonal is a mathematical term which means "having similar angles". It occurs in several contexts:*Isogonal polygon, polyhedron, polytope or tiling.*Isogonal trajectory in curve theory.*Isogonal conjugate in triangle geometry.... |
|
Alternate names
- Tricantitruncated 5-orthoplex / tricantitruncated pentacross
- Great rhombated penteract (girn) (Jonathan Bowers)
Coordinates
The Cartesian coordinates of the vertices of an cantitruncated tesseract having an edge length of 2 are given by all permutations of coordinates and sign of: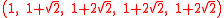
Bicantitruncated 5-cube
| Bicantitruncated 5-cube | |
|---|---|
| Type | uniform polyteron Uniform polyteron In geometry, a uniform polyteron is a five-dimensional uniform polytope. By definition, a uniform polyteron is vertex-transitive and constructed from uniform polychoron facets.... |
| Schläfli symbol | t1,2,3{3,3,3,4} t1,2,3{3,31,1} |
| Coxeter-Dynkin diagram Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... s |
|
| 4-faces | 122 |
| Cells | 840 |
| Faces | 2160 |
| Edges | 2400 |
| Vertices | 960 |
| Vertex figure Vertex figure In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:... |
|
| Coxeter group Coxeter group In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example... s |
BC5, [3,3,3,4] D5, [32,1,1] |
| Properties | convex Convex polytope A convex polytope is a special case of a polytope, having the additional property that it is also a convex set of points in the n-dimensional space Rn... |
Alternate names
- Bicantitruncated penteract
- Bicantitruncated pentacross
- Great birhombated penteractitriacontiditeron (Acronym: gibrant) (Jonathan Bowers)
Coordinates
Cartesian coordinates for the vertices of a cantitruncated 5-cube, centered at the origin, are all sign and coordinate permutationPermutation
In mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
s of
- (±3,±3,±2,±1,0)
Related polytopes
These polytopes are from a set of 31 uniform polytera generated from the regular 5-cube or 5-orthoplex.External links
- Polytopes of Various Dimensions, Jonathan Bowers
- Runcinated uniform polytera (spid), Jonathan Bowers
- Multi-dimensional Glossary

