
Demipenteract
Encyclopedia
| Demipenteract (5-demicube) |
||
|---|---|---|
 Petrie polygon Petrie polygon In geometry, a Petrie polygon for a regular polytope of n dimensions is a skew polygon such that every consecutive sides belong to one of the facets... projection |
||
| Type | Uniform 5-polytope | |
| Family (Dn) | 5-demicube | |
| Families (En) | k21 polytope 1k2 polytope Uniform 1 k2 polytope In geometry, 1k2 polytope is a uniform polytope in n-dimensions constructed from the En Coxeter group. The family was named by Coxeter as 1k2 by its bifurcating Coxeter-Dynkin diagram, with a single ring on the end of the 1-node sequence... |
|
| Coxeter symbol | 121 | |
| Schläfli symbol | {31,2,1} h{4,3,3,3} s{2,2,2,2} |
|
| Coxeter-Dynkin diagram Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... |
||
|-
|bgcolor=#e7dcc3|4-faces||26||10 {31,1,1}
16-cell
In four dimensional geometry, a 16-cell or hexadecachoron is a regular convex 4-polytope. It is one of the six regular convex 4-polytopes first described by the Swiss mathematician Ludwig Schläfli in the mid-19th century....
16 {3,3,3}
|-
|bgcolor=#e7dcc3|Cells||120||40 {31,0,1}
Tetrahedron
In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...
80 {3,3}
Tetrahedron
In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...
|-
|bgcolor=#e7dcc3|Faces||160||{3}
Triangle
A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....
|-
|bgcolor=#e7dcc3|Edges||80
|-
|bgcolor=#e7dcc3|Vertices||16
|-
|bgcolor=#e7dcc3|Vertex figure
Vertex figure
In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:...
|colspan=2|
rectified 5-cell
Rectified 5-cell
In four dimensional geometry, the rectified 5-cell is a uniform polychoron composed of 5 regular tetrahedral and 5 regular octahedral cells. Each edge has one tetrahedron and two octahedra. Each vertex has two tetrahedra and three octahedra. In total it has 30 triangle faces, 30 edges, and 10...
|-
|bgcolor=#e7dcc3|Petrie polygon
Petrie polygon
In geometry, a Petrie polygon for a regular polytope of n dimensions is a skew polygon such that every consecutive sides belong to one of the facets...
|colspan=2|Octagon
|-
|bgcolor=#e7dcc3|Symmetry group
Coxeter notation
In geometry, Coxeter notation is a system of classifying symmetry groups, describing the angles between with fundamental reflections of a Coxeter group. It uses a bracketed notation, with modifiers to indicate certain subgroups. The notation is named after H. S. M...
|colspan=2|D5, [34,1,1] = [1+,4,33]
[24]+
|-
|bgcolor=#e7dcc3|Properties
|colspan=2|convex
Convex polytope
A convex polytope is a special case of a polytope, having the additional property that it is also a convex set of points in the n-dimensional space Rn...
|}
In five dimensional geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, a demipenteract or 5-demicube is a semiregular 5-polytope
5-polytope
In five-dimensional geometry, a 5-polytope is a 5-dimensional polytope, bounded by facets. Each polyhedral cell being shared by exactly two polychoron facets. A proposed name for 5-polytopes is polyteron.-Definition:...
, constructed from a 5-hypercube (penteract
Penteract
In five dimensional geometry, a 5-cube is a name for a five dimensional hypercube with 32 vertices, 80 edges, 80 square faces, 40 cubic cells, and 10 tesseract hypercells....
) with alternated vertices deleted.
It was discovered by Thorold Gosset
Thorold Gosset
Thorold Gosset was an English lawyer and an amateur mathematician. In mathematics, he is noted for discovering and classifying the semiregular polytopes in dimensions four and higher.According to H. S. M...
. Since it was the only semiregular 5-polytope (made of more than one type of regular hypercell), he called it a 5-ic semi-regular.
Coxeter named this polytope as 121 from its Coxeter-Dynkin diagram
Coxeter-Dynkin diagram
In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors...
, which has branches of length 2, 1 and 1 with a ringed node on one of the short branches. It exists in the k21 polytope family as 121 with the Gosset polytopes: 221
Gosset 2 21 polytope
In 6-dimensional geometry, the 221 polytope is a uniform 6-polytope, constructed within the symmetry of the E6 group. It was discovered by Thorold Gosset, published in his 1900 paper. He called it an 6-ic semi-regular figure....
, 321
Gosset 3 21 polytope
In 7-dimensional geometry, the 321 polytope is a uniform 6-polytope, constructed within the symmetry of the E7 group. It was discovered by Thorold Gosset, published in his 1900 paper...
, and 421
Gosset 4 21 polytope
In 8-dimensional geometry, the 421 is a semiregular uniform 8-polytope, constructed within the symmetry of the E8 group. It was discovered by Thorold Gosset, published in his 1900 paper...
.
Cartesian coordinates
Cartesian coordinates for the vertices of a demipenteract centered at the origin and edge length 2√2 are alternate halves of the penteractPenteract
In five dimensional geometry, a 5-cube is a name for a five dimensional hypercube with 32 vertices, 80 edges, 80 square faces, 40 cubic cells, and 10 tesseract hypercells....
:
- (±1,±1,±1,±1,±1)
with an odd number of plus signs.
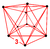
Projected images
 Perspective projection. |
Related polytopes
It is a part of a dimensional family of uniform polytopeUniform polytope
A uniform polytope is a vertex-transitive polytope made from uniform polytope facets of a lower dimension. Uniform polytopes of 2 dimensions are the regular polygons....
s called demihypercubes for being alternation of the hypercube
Hypercube
In geometry, a hypercube is an n-dimensional analogue of a square and a cube . It is a closed, compact, convex figure whose 1-skeleton consists of groups of opposite parallel line segments aligned in each of the space's dimensions, perpendicular to each other and of the same length.An...
family.
There are 23 uniform polytera
Uniform polyteron
In geometry, a uniform polyteron is a five-dimensional uniform polytope. By definition, a uniform polyteron is vertex-transitive and constructed from uniform polychoron facets....
(uniform 5-polytope) that can be constructed from the D5 symmetry of the demipenteract, 8 of which are unique to this family, and 15 are shared within the penteract
Penteract
In five dimensional geometry, a 5-cube is a name for a five dimensional hypercube with 32 vertices, 80 edges, 80 square faces, 40 cubic cells, and 10 tesseract hypercells....
ic family.

