Dynkin diagrams

Finite
E3=A2xA1
E4=A4
E5=D5
E6
E7
E8
Affine (Extended)
E9 or E8(1) or E8+
Hyperbolic (Over-extended)
E10 or E8(1)^ or E8++
Lorentzian algebras (Very-extended+)
E11 or E8+++
E12 or E8++++
...

In mathematics

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, especially in Lie

Lie algebra

In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...

 theory, E_n is the Kac–Moody algebra

Kac–Moody algebra

In mathematics, a Kac–Moody algebra is a Lie algebra, usually infinite-dimensional, that can be defined by generators and relations through a generalized Cartan matrix...

 whose Dynkin diagram is a bifurcating graph with three branches of length 1,2, and k, with k=n-4.

In some older books and papers, E₂ and E₄ are used as names for G₂ and F₄.

Finite dimensional Lie algebras

The E_n group is similar to the A_n group, except the nth node is connected to the 3rd node. So the Cartan matrix

Cartan matrix

In mathematics, the term Cartan matrix has three meanings. All of these are named after the French mathematician Élie Cartan. In fact, Cartan matrices in the context of Lie algebras were first investigated by Wilhelm Killing, whereas the Killing form is due to Cartan.- Lie algebras :A generalized...

 appears similar, -1 above and below the diagonal, except for the last row and column, have -1 in the third row and column.

• E₃ is another name for the Lie algebra A₁A₂ of dimension 11.

  

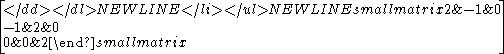
  • E₄ is another name for the Lie algebra A₄ of dimension 24.

    

    • E₅ is another name for the Lie algebra D₅ of dimension 45.

      

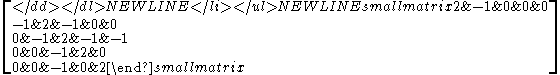
      • E₆ is the exceptional Lie algebra of dimension 78.

        

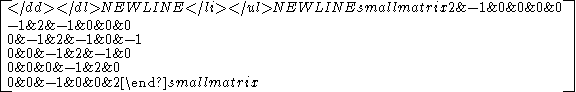
        • E₇ is the exceptional Lie algebra of dimension 133.

          

          • E₈
            E8 (mathematics)
            In mathematics, E8 is any of several closely related exceptional simple Lie groups, linear algebraic groups or Lie algebras of dimension 248; the same notation is used for the corresponding root lattice, which has rank 8...
            
            is the exceptional Lie algebra of dimension 248.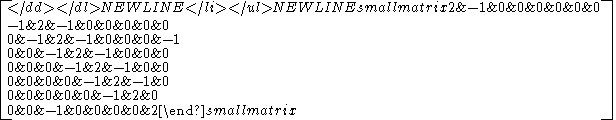

            
            

            Infinite dimensional Lie algebras

            • E₉ is another name for the infinite dimensional affine Lie algebra
              Affine Lie algebra
              In mathematics, an affine Lie algebra is an infinite-dimensional Lie algebra that is constructed in a canonical fashion out of a finite-dimensional simple Lie algebra. It is a Kac–Moody algebra for which the generalized Cartan matrix is positive semi-definite and has corank 1...
              
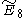                (also as E₈⁺ or E₈⁽¹⁾ as a (one-node) extended E₈) (or E8 lattice
              E8 lattice
              In mathematics, the E8 lattice is a special lattice in R8. It can be characterized as the unique positive-definite, even, unimodular lattice of rank 8...
              
              ) corresponding to the Lie algebra of type E₈
              E8 (mathematics)
              In mathematics, E8 is any of several closely related exceptional simple Lie groups, linear algebraic groups or Lie algebras of dimension 248; the same notation is used for the corresponding root lattice, which has rank 8...
              
              
            • E₁₀ (or E₈⁺⁺ or E₈^{(1)^} as a (two-node) over-extended E₈) is an infinite dimensional Kac–Moody algebra
              Kac–Moody algebra
              In mathematics, a Kac–Moody algebra is a Lie algebra, usually infinite-dimensional, that can be defined by generators and relations through a generalized Cartan matrix...
              
               whose root lattice is the even Lorentzian unimodular lattice
              Unimodular lattice
              In mathematics, a unimodular lattice is a lattice of determinant 1 or −1.The E8 lattice and the Leech lattice are two famous examples.- Definitions :...
              
               II_9,1 of dimension 10. Some of its root multiplicities have been calculated; for small roots the multiplicities seem to be well behaved, but for larger roots the observed patterns break down.
            • E₁₁ (or E₈⁺⁺⁺ as a (three-node) very-extended E₈) is an infinite dimensional Kac–Moody algebra
              Kac–Moody algebra
              In mathematics, a Kac–Moody algebra is a Lie algebra, usually infinite-dimensional, that can be defined by generators and relations through a generalized Cartan matrix...
              
               that has been conjectured to generate the symmetry "group" of M-theory
              M-theory
              In theoretical physics, M-theory is an extension of string theory in which 11 dimensions are identified. Because the dimensionality exceeds that of superstring theories in 10 dimensions, proponents believe that the 11-dimensional theory unites all five string theories...
              
              .
            • E_n for n≥12 is an infinite dimensional Kac–Moody algebra
              Kac–Moody algebra
              In mathematics, a Kac–Moody algebra is a Lie algebra, usually infinite-dimensional, that can be defined by generators and relations through a generalized Cartan matrix...
              
               that has not been studied much.

            
            

            Root lattice

            The root lattice of E_n has determinant 9−n, and can be constructed as the
            lattice of vectors in the unimodular Lorentzian lattice

            Unimodular lattice

            In mathematics, a unimodular lattice is a lattice of determinant 1 or −1.The E8 lattice and the Leech lattice are two famous examples.- Definitions :...

            
             Z_n,1 that are orthogonal to the vector (1,1,1,1,....,1|3) of norm n×1² − 3² = n − 9.
            

            E7½

            Landsberg and Manivel extended the definition of E_n for integer n to include the case n = 7½. They did this in order to fill the "hole" in dimension formulae for representations of the E_n series which was observed by Cvitanovic, Deligne, Cohen and de Man. E_7½ has dimension 190, but is not a simple Lie algebra: it contains a 57 dimensional Heisenberg algebra as its nilradical.
            

            See also

            • k₂₁, 2_k1
              Uniform 2 k1 polytope
              In geometry, 2k1 polytope is a uniform polytope in n dimensions constructed from the En Coxeter group. The family was named by Coxeter as 2k1 by its bifurcating Coxeter-Dynkin diagram, with a single ring on the end of the 2-node sequence...
              
              , 1_k2
              Uniform 1 k2 polytope
              In geometry, 1k2 polytope is a uniform polytope in n-dimensions constructed from the En Coxeter group. The family was named by Coxeter as 1k2 by its bifurcating Coxeter-Dynkin diagram, with a single ring on the end of the 1-node sequence...
              
              polytopes based on E_n Lie algebras.

            
            

            Further reading

            Class.Quant.Grav. 18 (2001) 4443-4460 Guersey Memorial Conference Proceedings '94

            • Landsberg, J. M. Manivel, L. The sextonions and E_7½. Adv. Math. 201 (2006), no. 1, 143-179.
            • Connections between Kac-Moody algebras and M-theory, Paul P. Cook, 2006 http://academia.edu.documents.s3.amazonaws.com/1676492/0711.3498v1.pdf

            The source of this article is wikipedia, the free encyclopedia.  The text of this article is licensed under the GFDL.