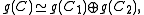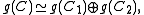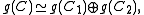Kac–Moody algebra
Encyclopedia
In mathematics
, a Kac–Moody algebra (named for Victor Kac
and Robert Moody
, who independently discovered them) is a Lie algebra
, usually infinite-dimensional, that can be defined by generators and relations through a generalized Cartan matrix. These algebras form a generalization of finite-dimensional semisimple Lie algebras, and many properties related to the structure of a Lie algebra such as its root system
, irreducible representations
, and connection to flag manifold
s have natural analogues in the Kac–Moody setting.
A class of Kac–Moody algebras called affine Lie algebra
s is of particular importance in mathematics and theoretical physics
, especially conformal field theory
and the theory of exactly solvable models. Kac discovered an elegant proof of certain combinatorial identities, Macdonald
identities
, which is based on the representation theory of affine Kac–Moody algebras. Howard Garland and James Lepowsky
demonstrated that Rogers-Ramanujan identities
can be derived in a similar fashion.
and Wilhelm Killing
of finite dimensional simple Lie algebras from the Cartan integers was type dependent. In 1966 Jean-Pierre Serre
showed that relations of Claude Chevalley
and Harish-Chandra
, with simplifications by Nathan Jacobson
, give a defining presentation for the Lie algebra
. One could thus describe a simple Lie algebra in terms of generators and relations using data from the matrix of Cartan integers, which is naturally positive definite.
In his 1967 thesis, Robert Moody
considered Lie algebras whose Cartan matrix
is no longer positive definite. This still gave rise to a Lie algebra, but one which is now infinite dimensional. Simultaneously, Z-graded Lie algebra
s were being studied in Moscow where I. L. Kantor introduced and studied a general class of Lie algebras including what eventually became known as Kac–Moody algebras. Victor Kac
was also studying simple or nearly simple Lie algebras with polynomial growth. A rich mathematical theory of infinite dimensional Lie algebras evolved. An account of the subject, which also includes works of many others is given in (Kac 1990). See also (Seligman 1987).
The Kac–Moody algebra is the Lie algebra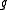 defined by generators
defined by generators
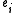 and
and 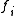 and the elements of
and the elements of 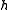 and relations
and relations
where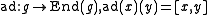 is the adjoint representation of
is the adjoint representation of 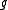 .
.
A real
(possibly infinite-dimensional) Lie algebra
is also considered a Kac–Moody algebra if its complexification
is a Kac–Moody algebra.
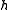 is a Cartan subalgebra of the Kac–Moody algebra.
is a Cartan subalgebra of the Kac–Moody algebra.
If g is an element of the Kac–Moody algebra such that
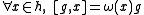
where ω is an element of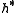 , then g is said to have weight ω. The Kac–Moody algebra can be diagonalized into weight eigenvectors. The Cartan subalgebra h has weight zero, ei has weight α*i and fi has weight −α*i. If the Lie bracket
, then g is said to have weight ω. The Kac–Moody algebra can be diagonalized into weight eigenvectors. The Cartan subalgebra h has weight zero, ei has weight α*i and fi has weight −α*i. If the Lie bracket
of two weight eigenvectors is nonzero, then its weight is the sum of their weights. The condition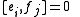 for
for 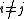 simply means the α*i are simple root
simply means the α*i are simple root
s.
where the two Kac–Moody algebras in the right hand side are associated with the submatrices of C corresponding to the index sets I1 and I2.
An important subclass of Kac–Moody algebras corresponds to symmetrizable generalized Cartan matrices C, which can be decomposed as DS, where D is a diagonal matrix
with positive integer entries and S is a symmetric matrix. Under the assumptions that C is symmetrizable and indecomposable, the Kac–Moody algebras are divided into three classes:
Symmetrizable indecomposable generalized Cartan matrices of finite and affine type have been completely classified. They correspond to Dynkin diagrams and affine Dynkin diagrams. Very little is known about the Kac–Moody algebras of indefinite type. Among those, the main focus has been on the (generalized) Kac–Moody algebras of hyperbolic type, for which the matrix S is indefinite, but for each proper subset of I, the corresponding submatrix is positive definite or positive semidefinite. Such matrices have rank at most 10 and have also been completely determined.
In mathematics
, a Kac–Moody algebra (named for Victor Kac
and Robert Moody
, who independently discovered them) is a Lie algebra
, usually infinite-dimensional, that can be defined by generators and relations through a generalized Cartan matrix. These algebras form a generalization of finite-dimensional semisimple Lie algebras, and many properties related to the structure of a Lie algebra such as its root system
, irreducible representations
, and connection to flag manifold
s have natural analogues in the Kac–Moody setting.
A class of Kac–Moody algebras called affine Lie algebra
s is of particular importance in mathematics and theoretical physics
, especially conformal field theory
and the theory of exactly solvable models. Kac discovered an elegant proof of certain combinatorial identities, Macdonald
identities
, which is based on the representation theory of affine Kac–Moody algebras. Howard Garland and James Lepowsky
demonstrated that Rogers-Ramanujan identities
can be derived in a similar fashion.
and Wilhelm Killing
of finite dimensional simple Lie algebras from the Cartan integers was type dependent. In 1966 Jean-Pierre Serre
showed that relations of Claude Chevalley
and Harish-Chandra
, with simplifications by Nathan Jacobson
, give a defining presentation for the Lie algebra
. One could thus describe a simple Lie algebra in terms of generators and relations using data from the matrix of Cartan integers, which is naturally positive definite.
In his 1967 thesis, Robert Moody
considered Lie algebras whose Cartan matrix
is no longer positive definite. This still gave rise to a Lie algebra, but one which is now infinite dimensional. Simultaneously, Z-graded Lie algebra
s were being studied in Moscow where I. L. Kantor introduced and studied a general class of Lie algebras including what eventually became known as Kac–Moody algebras. Victor Kac
was also studying simple or nearly simple Lie algebras with polynomial growth. A rich mathematical theory of infinite dimensional Lie algebras evolved. An account of the subject, which also includes works of many others is given in (Kac 1990). See also (Seligman 1987).
The Kac–Moody algebra is the Lie algebra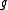 defined by generators
defined by generators
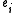 and
and 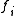 and the elements of
and the elements of 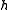 and relations
and relations
where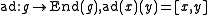 is the adjoint representation of
is the adjoint representation of 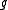 .
.
A real
(possibly infinite-dimensional) Lie algebra
is also considered a Kac–Moody algebra if its complexification
is a Kac–Moody algebra.
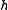 is a Cartan subalgebra of the Kac–Moody algebra.
is a Cartan subalgebra of the Kac–Moody algebra.
If g is an element of the Kac–Moody algebra such that
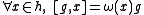
where ω is an element of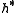 , then g is said to have weight ω. The Kac–Moody algebra can be diagonalized into weight eigenvectors. The Cartan subalgebra h has weight zero, ei has weight α*i and fi has weight −α*i. If the Lie bracket
, then g is said to have weight ω. The Kac–Moody algebra can be diagonalized into weight eigenvectors. The Cartan subalgebra h has weight zero, ei has weight α*i and fi has weight −α*i. If the Lie bracket
of two weight eigenvectors is nonzero, then its weight is the sum of their weights. The condition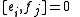 for
for 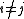 simply means the α*i are simple root
simply means the α*i are simple root
s.
where the two Kac–Moody algebras in the right hand side are associated with the submatrices of C corresponding to the index sets I1 and I2.
An important subclass of Kac–Moody algebras corresponds to symmetrizable generalized Cartan matrices C, which can be decomposed as DS, where D is a diagonal matrix
with positive integer entries and S is a symmetric matrix. Under the assumptions that C is symmetrizable and indecomposable, the Kac–Moody algebras are divided into three classes:
Symmetrizable indecomposable generalized Cartan matrices of finite and affine type have been completely classified. They correspond to Dynkin diagrams and affine Dynkin diagrams. Very little is known about the Kac–Moody algebras of indefinite type. Among those, the main focus has been on the (generalized) Kac–Moody algebras of hyperbolic type, for which the matrix S is indefinite, but for each proper subset of I, the corresponding submatrix is positive definite or positive semidefinite. Such matrices have rank at most 10 and have also been completely determined.
In mathematics
, a Kac–Moody algebra (named for Victor Kac
and Robert Moody
, who independently discovered them) is a Lie algebra
, usually infinite-dimensional, that can be defined by generators and relations through a generalized Cartan matrix. These algebras form a generalization of finite-dimensional semisimple Lie algebras, and many properties related to the structure of a Lie algebra such as its root system
, irreducible representations
, and connection to flag manifold
s have natural analogues in the Kac–Moody setting.
A class of Kac–Moody algebras called affine Lie algebra
s is of particular importance in mathematics and theoretical physics
, especially conformal field theory
and the theory of exactly solvable models. Kac discovered an elegant proof of certain combinatorial identities, Macdonald
identities
, which is based on the representation theory of affine Kac–Moody algebras. Howard Garland and James Lepowsky
demonstrated that Rogers-Ramanujan identities
can be derived in a similar fashion.
and Wilhelm Killing
of finite dimensional simple Lie algebras from the Cartan integers was type dependent. In 1966 Jean-Pierre Serre
showed that relations of Claude Chevalley
and Harish-Chandra
, with simplifications by Nathan Jacobson
, give a defining presentation for the Lie algebra
. One could thus describe a simple Lie algebra in terms of generators and relations using data from the matrix of Cartan integers, which is naturally positive definite.
In his 1967 thesis, Robert Moody
considered Lie algebras whose Cartan matrix
is no longer positive definite. This still gave rise to a Lie algebra, but one which is now infinite dimensional. Simultaneously, Z-graded Lie algebra
s were being studied in Moscow where I. L. Kantor introduced and studied a general class of Lie algebras including what eventually became known as Kac–Moody algebras. Victor Kac
was also studying simple or nearly simple Lie algebras with polynomial growth. A rich mathematical theory of infinite dimensional Lie algebras evolved. An account of the subject, which also includes works of many others is given in (Kac 1990). See also (Seligman 1987).
The Kac–Moody algebra is the Lie algebra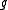 defined by generators
defined by generators
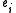 and
and 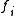 and the elements of
and the elements of 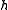 and relations
and relations
where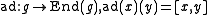 is the adjoint representation of
is the adjoint representation of 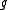 .
.
A real
(possibly infinite-dimensional) Lie algebra
is also considered a Kac–Moody algebra if its complexification
is a Kac–Moody algebra.
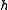 is a Cartan subalgebra of the Kac–Moody algebra.
is a Cartan subalgebra of the Kac–Moody algebra.
If g is an element of the Kac–Moody algebra such that
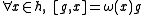
where ω is an element of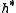 , then g is said to have weight ω. The Kac–Moody algebra can be diagonalized into weight eigenvectors. The Cartan subalgebra h has weight zero, ei has weight α*i and fi has weight −α*i. If the Lie bracket
, then g is said to have weight ω. The Kac–Moody algebra can be diagonalized into weight eigenvectors. The Cartan subalgebra h has weight zero, ei has weight α*i and fi has weight −α*i. If the Lie bracket
of two weight eigenvectors is nonzero, then its weight is the sum of their weights. The condition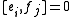 for
for 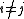 simply means the α*i are simple root
simply means the α*i are simple root
s.
where the two Kac–Moody algebras in the right hand side are associated with the submatrices of C corresponding to the index sets I1 and I2.
An important subclass of Kac–Moody algebras corresponds to symmetrizable generalized Cartan matrices C, which can be decomposed as DS, where D is a diagonal matrix
with positive integer entries and S is a symmetric matrix. Under the assumptions that C is symmetrizable and indecomposable, the Kac–Moody algebras are divided into three classes:
Symmetrizable indecomposable generalized Cartan matrices of finite and affine type have been completely classified. They correspond to Dynkin diagrams and affine Dynkin diagrams. Very little is known about the Kac–Moody algebras of indefinite type. Among those, the main focus has been on the (generalized) Kac–Moody algebras of hyperbolic type, for which the matrix S is indefinite, but for each proper subset of I, the corresponding submatrix is positive definite or positive semidefinite. Such matrices have rank at most 10 and have also been completely determined.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a Kac–Moody algebra (named for Victor Kac
Victor Kac
Victor G. Kac is a Soviet and American mathematician at MIT, known for his work in representation theory. He discovered Kac–Moody algebras, and used the Weyl–Kac character formula for them to reprove the Macdonald identities...
and Robert Moody
Robert Moody
Robert Vaughan Moody, OC, FRSC is a Canadian mathematician. He is the co-discover of Kac-Moody algebra, a Lie algebra, usually infinite-dimensional, that can be defined through a generalized root system....
, who independently discovered them) is a Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
, usually infinite-dimensional, that can be defined by generators and relations through a generalized Cartan matrix. These algebras form a generalization of finite-dimensional semisimple Lie algebras, and many properties related to the structure of a Lie algebra such as its root system
Root system
In mathematics, a root system is a configuration of vectors in a Euclidean space satisfying certain geometrical properties. The concept is fundamental in the theory of Lie groups and Lie algebras...
, irreducible representations
Representation of a Lie algebra
In the mathematical field of representation theory, a Lie algebra representation or representation of a Lie algebra is a way of writing a Lie algebra as a set of matrices in such a way that the Lie bracket is given by the commutator.The notion is closely related to that of a representation of a...
, and connection to flag manifold
Flag manifold
In mathematics, a generalized flag variety is a homogeneous space whose points are flags in a finite-dimensional vector space V over a field F. When F is the real or complex numbers, a generalized flag variety is a smooth or complex manifold, called a real or complex flag manifold...
s have natural analogues in the Kac–Moody setting.
A class of Kac–Moody algebras called affine Lie algebra
Affine Lie algebra
In mathematics, an affine Lie algebra is an infinite-dimensional Lie algebra that is constructed in a canonical fashion out of a finite-dimensional simple Lie algebra. It is a Kac–Moody algebra for which the generalized Cartan matrix is positive semi-definite and has corank 1...
s is of particular importance in mathematics and theoretical physics
Theoretical physics
Theoretical physics is a branch of physics which employs mathematical models and abstractions of physics to rationalize, explain and predict natural phenomena...
, especially conformal field theory
Conformal field theory
A conformal field theory is a quantum field theory that is invariant under conformal transformations...
and the theory of exactly solvable models. Kac discovered an elegant proof of certain combinatorial identities, Macdonald
Ian G. Macdonald
Ian Grant Macdonald is a British mathematician known for his contributions to symmetric functions, special functions, Lie algebra theory and other aspects of algebraic combinatorics ....
identities
Macdonald identities
In mathematics, the Macdonald identities are some infinite product identities associated to affine root systems, introduced by . They include as special cases the Jacobi triple product identity, Watson's quintuple product identity, several identities found by , and a 10-fold product identity found...
, which is based on the representation theory of affine Kac–Moody algebras. Howard Garland and James Lepowsky
James Lepowsky
James Lepowsky is a professor of mathematics at Rutgers University, New Jersey. Previously he taught at Yale University. He received his Ph.D from M.I.T. in 1970 where his advisor was Bertram Kostant. Lepowsky graduated from Stuyvesant High School in 1961, 16 years after Kostant...
demonstrated that Rogers-Ramanujan identities
Rogers-Ramanujan identities
In mathematics, the Rogers–Ramanujan identities are two identities related to basic hypergeometric series, first discovered and proved by . They were subsequently rediscovered by Srinivasa Ramanujan some time before 1913. Ramanujan had no proof, but rediscovered Rogers's paper in 1917, and they...
can be derived in a similar fashion.
History of Kac-Moody algebras
The initial construction by Élie CartanÉlie Cartan
Élie Joseph Cartan was an influential French mathematician, who did fundamental work in the theory of Lie groups and their geometric applications...
and Wilhelm Killing
Wilhelm Killing
Wilhelm Karl Joseph Killing was a German mathematician who made important contributions to the theories of Lie algebras, Lie groups, and non-Euclidean geometry....
of finite dimensional simple Lie algebras from the Cartan integers was type dependent. In 1966 Jean-Pierre Serre
Jean-Pierre Serre
Jean-Pierre Serre is a French mathematician. He has made contributions in the fields of algebraic geometry, number theory, and topology.-Early years:...
showed that relations of Claude Chevalley
Claude Chevalley
Claude Chevalley was a French mathematician who made important contributions to number theory, algebraic geometry, class field theory, finite group theory, and the theory of algebraic groups...
and Harish-Chandra
Harish-Chandra
Harish-Chandra was an Indian mathematician, who did fundamental work in representation theory, especially Harmonic analysis on semisimple Lie groups. -Life:...
, with simplifications by Nathan Jacobson
Nathan Jacobson
Nathan Jacobson was an American mathematician....
, give a defining presentation for the Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
. One could thus describe a simple Lie algebra in terms of generators and relations using data from the matrix of Cartan integers, which is naturally positive definite.
In his 1967 thesis, Robert Moody
Robert Moody
Robert Vaughan Moody, OC, FRSC is a Canadian mathematician. He is the co-discover of Kac-Moody algebra, a Lie algebra, usually infinite-dimensional, that can be defined through a generalized root system....
considered Lie algebras whose Cartan matrix
Cartan matrix
In mathematics, the term Cartan matrix has three meanings. All of these are named after the French mathematician Élie Cartan. In fact, Cartan matrices in the context of Lie algebras were first investigated by Wilhelm Killing, whereas the Killing form is due to Cartan.- Lie algebras :A generalized...
is no longer positive definite. This still gave rise to a Lie algebra, but one which is now infinite dimensional. Simultaneously, Z-graded Lie algebra
Graded Lie algebra
In mathematics, a graded Lie algebra is a Lie algebra endowed with a gradation which is compatible with the Lie bracket. In other words, a graded Lie algebra is a Lie algebra which is also a nonassociative graded algebra under the bracket operation. A choice of Cartan decomposition endows any...
s were being studied in Moscow where I. L. Kantor introduced and studied a general class of Lie algebras including what eventually became known as Kac–Moody algebras. Victor Kac
Victor Kac
Victor G. Kac is a Soviet and American mathematician at MIT, known for his work in representation theory. He discovered Kac–Moody algebras, and used the Weyl–Kac character formula for them to reprove the Macdonald identities...
was also studying simple or nearly simple Lie algebras with polynomial growth. A rich mathematical theory of infinite dimensional Lie algebras evolved. An account of the subject, which also includes works of many others is given in (Kac 1990). See also (Seligman 1987).
Definition
A Kac–Moody algebra is given by the following:- An n×n generalized Cartan matrix of rankRank (linear algebra)The column rank of a matrix A is the maximum number of linearly independent column vectors of A. The row rank of a matrix A is the maximum number of linearly independent row vectors of A...
r. - A vector spaceVector spaceA vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
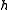 over the complex numberComplex numberA complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
over the complex numberComplex numberA complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s of dimension 2n − r. - A set of n linearly independent elements
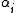 of
of 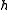 and a set of n linearly independent elements
and a set of n linearly independent elements 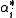 of the dual spaceDual spaceIn mathematics, any vector space, V, has a corresponding dual vector space consisting of all linear functionals on V. Dual vector spaces defined on finite-dimensional vector spaces can be used for defining tensors which are studied in tensor algebra...
of the dual spaceDual spaceIn mathematics, any vector space, V, has a corresponding dual vector space consisting of all linear functionals on V. Dual vector spaces defined on finite-dimensional vector spaces can be used for defining tensors which are studied in tensor algebra...
, such that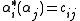 . The
. The 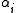 are known as coroots, while the
are known as coroots, while the 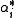 are known as roots.
are known as roots.
The Kac–Moody algebra is the Lie algebra
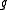 defined by generators
defined by generatorsGenerating set
In mathematics, the expressions generator, generate, generated by and generating set can have several closely related technical meanings:...
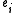 and
and 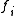 and the elements of
and the elements of 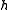 and relations
and relations
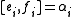
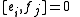 for
for 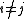
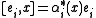 , for
, for 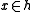
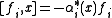 , for
, for 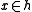
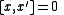 for
for 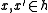
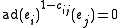
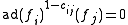
where
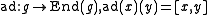 is the adjoint representation of
is the adjoint representation of 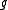 .
.A real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
(possibly infinite-dimensional) Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
is also considered a Kac–Moody algebra if its complexification
Complexification
In mathematics, the complexification of a real vector space V is a vector space VC over the complex number field obtained by formally extending scalar multiplication to include multiplication by complex numbers. Any basis for V over the real numbers serves as a basis for VC over the complex...
is a Kac–Moody algebra.
Interpretation
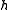 is a Cartan subalgebra of the Kac–Moody algebra.
is a Cartan subalgebra of the Kac–Moody algebra.If g is an element of the Kac–Moody algebra such that
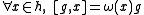
where ω is an element of
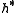 , then g is said to have weight ω. The Kac–Moody algebra can be diagonalized into weight eigenvectors. The Cartan subalgebra h has weight zero, ei has weight α*i and fi has weight −α*i. If the Lie bracket
, then g is said to have weight ω. The Kac–Moody algebra can be diagonalized into weight eigenvectors. The Cartan subalgebra h has weight zero, ei has weight α*i and fi has weight −α*i. If the Lie bracketLie bracket of vector fields
In the mathematical field of differential topology, the Lie bracket of vector fields, Jacobi–Lie bracket, or commutator of vector fields is a bilinear differential operator which assigns, to any two vector fields X and Y on a smooth manifold M, a third vector field denoted [X, Y]...
of two weight eigenvectors is nonzero, then its weight is the sum of their weights. The condition
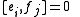 for
for 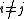 simply means the α*i are simple root
simply means the α*i are simple rootSimple root
in mathematics the term simple root can refer to one of two unrelated notions:*A simple root of a polynomial is a root of multiplicity one*A simple root in a root system is a member of a subset determined by a choice of positive roots...
s.
Types of Kac–Moody algebras
Properties of a Kac–Moody algebra are controlled by the algebraic properties of its generalized Cartan matrix C. In order to classify Kac–Moody algebras, it is enough to consider the case of an indecomposable matrixC, that is, assume that there is no decomposition of the set of indices I into a disjoint union of non-empty subsets I1 and I2 such that Cij = 0 for all i in I1 and j in I2. Any decomposition of the generalized Cartan matrix leads to the direct sum decomposition of the corresponding Kac–Moody algebra:where the two Kac–Moody algebras in the right hand side are associated with the submatrices of C corresponding to the index sets I1 and I2.
An important subclass of Kac–Moody algebras corresponds to symmetrizable generalized Cartan matrices C, which can be decomposed as DS, where D is a diagonal matrix
Diagonal matrix
In linear algebra, a diagonal matrix is a matrix in which the entries outside the main diagonal are all zero. The diagonal entries themselves may or may not be zero...
with positive integer entries and S is a symmetric matrix. Under the assumptions that C is symmetrizable and indecomposable, the Kac–Moody algebras are divided into three classes:
- A positive definite matrix S gives rise to a finite-dimensional simple Lie algebra.
- A positive semidefinite matrix S gives rise to an infinite-dimensional Kac–Moody algebra of affine type, or an affine Lie algebraAffine Lie algebraIn mathematics, an affine Lie algebra is an infinite-dimensional Lie algebra that is constructed in a canonical fashion out of a finite-dimensional simple Lie algebra. It is a Kac–Moody algebra for which the generalized Cartan matrix is positive semi-definite and has corank 1...
. - An indefinite matrix S gives rise to a Kac–Moody algebra of indefinite type.
- Since the diagonal entries of C and S are positive, S cannot be negative definite or negative semidefinite.
Symmetrizable indecomposable generalized Cartan matrices of finite and affine type have been completely classified. They correspond to Dynkin diagrams and affine Dynkin diagrams. Very little is known about the Kac–Moody algebras of indefinite type. Among those, the main focus has been on the (generalized) Kac–Moody algebras of hyperbolic type, for which the matrix S is indefinite, but for each proper subset of I, the corresponding submatrix is positive definite or positive semidefinite. Such matrices have rank at most 10 and have also been completely determined.
See also
- Weyl–Kac character formula
- Generalized Kac–Moody algebraGeneralized Kac–Moody algebraIn mathematics, a generalized Kac–Moody algebra is a Lie algebra that is similar to aKac–Moody algebra, except that it is allowed to have imaginary simple roots.Generalized Kac–Moody algebras are also sometimes called GKM algebras,...
In mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a Kac–Moody algebra (named for Victor Kac
Victor Kac
Victor G. Kac is a Soviet and American mathematician at MIT, known for his work in representation theory. He discovered Kac–Moody algebras, and used the Weyl–Kac character formula for them to reprove the Macdonald identities...
and Robert Moody
Robert Moody
Robert Vaughan Moody, OC, FRSC is a Canadian mathematician. He is the co-discover of Kac-Moody algebra, a Lie algebra, usually infinite-dimensional, that can be defined through a generalized root system....
, who independently discovered them) is a Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
, usually infinite-dimensional, that can be defined by generators and relations through a generalized Cartan matrix. These algebras form a generalization of finite-dimensional semisimple Lie algebras, and many properties related to the structure of a Lie algebra such as its root system
Root system
In mathematics, a root system is a configuration of vectors in a Euclidean space satisfying certain geometrical properties. The concept is fundamental in the theory of Lie groups and Lie algebras...
, irreducible representations
Representation of a Lie algebra
In the mathematical field of representation theory, a Lie algebra representation or representation of a Lie algebra is a way of writing a Lie algebra as a set of matrices in such a way that the Lie bracket is given by the commutator.The notion is closely related to that of a representation of a...
, and connection to flag manifold
Flag manifold
In mathematics, a generalized flag variety is a homogeneous space whose points are flags in a finite-dimensional vector space V over a field F. When F is the real or complex numbers, a generalized flag variety is a smooth or complex manifold, called a real or complex flag manifold...
s have natural analogues in the Kac–Moody setting.
A class of Kac–Moody algebras called affine Lie algebra
Affine Lie algebra
In mathematics, an affine Lie algebra is an infinite-dimensional Lie algebra that is constructed in a canonical fashion out of a finite-dimensional simple Lie algebra. It is a Kac–Moody algebra for which the generalized Cartan matrix is positive semi-definite and has corank 1...
s is of particular importance in mathematics and theoretical physics
Theoretical physics
Theoretical physics is a branch of physics which employs mathematical models and abstractions of physics to rationalize, explain and predict natural phenomena...
, especially conformal field theory
Conformal field theory
A conformal field theory is a quantum field theory that is invariant under conformal transformations...
and the theory of exactly solvable models. Kac discovered an elegant proof of certain combinatorial identities, Macdonald
Ian G. Macdonald
Ian Grant Macdonald is a British mathematician known for his contributions to symmetric functions, special functions, Lie algebra theory and other aspects of algebraic combinatorics ....
identities
Macdonald identities
In mathematics, the Macdonald identities are some infinite product identities associated to affine root systems, introduced by . They include as special cases the Jacobi triple product identity, Watson's quintuple product identity, several identities found by , and a 10-fold product identity found...
, which is based on the representation theory of affine Kac–Moody algebras. Howard Garland and James Lepowsky
James Lepowsky
James Lepowsky is a professor of mathematics at Rutgers University, New Jersey. Previously he taught at Yale University. He received his Ph.D from M.I.T. in 1970 where his advisor was Bertram Kostant. Lepowsky graduated from Stuyvesant High School in 1961, 16 years after Kostant...
demonstrated that Rogers-Ramanujan identities
Rogers-Ramanujan identities
In mathematics, the Rogers–Ramanujan identities are two identities related to basic hypergeometric series, first discovered and proved by . They were subsequently rediscovered by Srinivasa Ramanujan some time before 1913. Ramanujan had no proof, but rediscovered Rogers's paper in 1917, and they...
can be derived in a similar fashion.
History of Kac-Moody algebras
The initial construction by Élie CartanÉlie Cartan
Élie Joseph Cartan was an influential French mathematician, who did fundamental work in the theory of Lie groups and their geometric applications...
and Wilhelm Killing
Wilhelm Killing
Wilhelm Karl Joseph Killing was a German mathematician who made important contributions to the theories of Lie algebras, Lie groups, and non-Euclidean geometry....
of finite dimensional simple Lie algebras from the Cartan integers was type dependent. In 1966 Jean-Pierre Serre
Jean-Pierre Serre
Jean-Pierre Serre is a French mathematician. He has made contributions in the fields of algebraic geometry, number theory, and topology.-Early years:...
showed that relations of Claude Chevalley
Claude Chevalley
Claude Chevalley was a French mathematician who made important contributions to number theory, algebraic geometry, class field theory, finite group theory, and the theory of algebraic groups...
and Harish-Chandra
Harish-Chandra
Harish-Chandra was an Indian mathematician, who did fundamental work in representation theory, especially Harmonic analysis on semisimple Lie groups. -Life:...
, with simplifications by Nathan Jacobson
Nathan Jacobson
Nathan Jacobson was an American mathematician....
, give a defining presentation for the Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
. One could thus describe a simple Lie algebra in terms of generators and relations using data from the matrix of Cartan integers, which is naturally positive definite.
In his 1967 thesis, Robert Moody
Robert Moody
Robert Vaughan Moody, OC, FRSC is a Canadian mathematician. He is the co-discover of Kac-Moody algebra, a Lie algebra, usually infinite-dimensional, that can be defined through a generalized root system....
considered Lie algebras whose Cartan matrix
Cartan matrix
In mathematics, the term Cartan matrix has three meanings. All of these are named after the French mathematician Élie Cartan. In fact, Cartan matrices in the context of Lie algebras were first investigated by Wilhelm Killing, whereas the Killing form is due to Cartan.- Lie algebras :A generalized...
is no longer positive definite. This still gave rise to a Lie algebra, but one which is now infinite dimensional. Simultaneously, Z-graded Lie algebra
Graded Lie algebra
In mathematics, a graded Lie algebra is a Lie algebra endowed with a gradation which is compatible with the Lie bracket. In other words, a graded Lie algebra is a Lie algebra which is also a nonassociative graded algebra under the bracket operation. A choice of Cartan decomposition endows any...
s were being studied in Moscow where I. L. Kantor introduced and studied a general class of Lie algebras including what eventually became known as Kac–Moody algebras. Victor Kac
Victor Kac
Victor G. Kac is a Soviet and American mathematician at MIT, known for his work in representation theory. He discovered Kac–Moody algebras, and used the Weyl–Kac character formula for them to reprove the Macdonald identities...
was also studying simple or nearly simple Lie algebras with polynomial growth. A rich mathematical theory of infinite dimensional Lie algebras evolved. An account of the subject, which also includes works of many others is given in (Kac 1990). See also (Seligman 1987).
Definition
A Kac–Moody algebra is given by the following:- An n×n generalized Cartan matrix of rankRank (linear algebra)The column rank of a matrix A is the maximum number of linearly independent column vectors of A. The row rank of a matrix A is the maximum number of linearly independent row vectors of A...
r. - A vector spaceVector spaceA vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
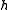 over the complex numberComplex numberA complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
over the complex numberComplex numberA complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s of dimension 2n − r. - A set of n linearly independent elements
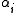 of
of 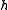 and a set of n linearly independent elements
and a set of n linearly independent elements 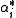 of the dual spaceDual spaceIn mathematics, any vector space, V, has a corresponding dual vector space consisting of all linear functionals on V. Dual vector spaces defined on finite-dimensional vector spaces can be used for defining tensors which are studied in tensor algebra...
of the dual spaceDual spaceIn mathematics, any vector space, V, has a corresponding dual vector space consisting of all linear functionals on V. Dual vector spaces defined on finite-dimensional vector spaces can be used for defining tensors which are studied in tensor algebra...
, such that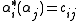 . The
. The 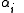 are known as coroots, while the
are known as coroots, while the 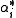 are known as roots.
are known as roots.
The Kac–Moody algebra is the Lie algebra
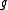 defined by generators
defined by generatorsGenerating set
In mathematics, the expressions generator, generate, generated by and generating set can have several closely related technical meanings:...
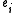 and
and 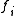 and the elements of
and the elements of 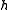 and relations
and relations
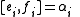
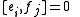 for
for 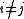
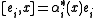 , for
, for 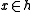
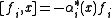 , for
, for 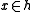
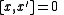 for
for 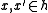
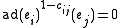
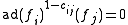
where
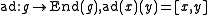 is the adjoint representation of
is the adjoint representation of 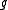 .
.A real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
(possibly infinite-dimensional) Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
is also considered a Kac–Moody algebra if its complexification
Complexification
In mathematics, the complexification of a real vector space V is a vector space VC over the complex number field obtained by formally extending scalar multiplication to include multiplication by complex numbers. Any basis for V over the real numbers serves as a basis for VC over the complex...
is a Kac–Moody algebra.
Interpretation
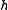 is a Cartan subalgebra of the Kac–Moody algebra.
is a Cartan subalgebra of the Kac–Moody algebra.If g is an element of the Kac–Moody algebra such that
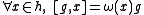
where ω is an element of
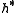 , then g is said to have weight ω. The Kac–Moody algebra can be diagonalized into weight eigenvectors. The Cartan subalgebra h has weight zero, ei has weight α*i and fi has weight −α*i. If the Lie bracket
, then g is said to have weight ω. The Kac–Moody algebra can be diagonalized into weight eigenvectors. The Cartan subalgebra h has weight zero, ei has weight α*i and fi has weight −α*i. If the Lie bracketLie bracket of vector fields
In the mathematical field of differential topology, the Lie bracket of vector fields, Jacobi–Lie bracket, or commutator of vector fields is a bilinear differential operator which assigns, to any two vector fields X and Y on a smooth manifold M, a third vector field denoted [X, Y]...
of two weight eigenvectors is nonzero, then its weight is the sum of their weights. The condition
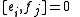 for
for 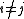 simply means the α*i are simple root
simply means the α*i are simple rootSimple root
in mathematics the term simple root can refer to one of two unrelated notions:*A simple root of a polynomial is a root of multiplicity one*A simple root in a root system is a member of a subset determined by a choice of positive roots...
s.
Types of Kac–Moody algebras
Properties of a Kac–Moody algebra are controlled by the algebraic properties of its generalized Cartan matrix C. In order to classify Kac–Moody algebras, it is enough to consider the case of an indecomposable matrixC, that is, assume that there is no decomposition of the set of indices I into a disjoint union of non-empty subsets I1 and I2 such that Cij = 0 for all i in I1 and j in I2. Any decomposition of the generalized Cartan matrix leads to the direct sum decomposition of the corresponding Kac–Moody algebra:where the two Kac–Moody algebras in the right hand side are associated with the submatrices of C corresponding to the index sets I1 and I2.
An important subclass of Kac–Moody algebras corresponds to symmetrizable generalized Cartan matrices C, which can be decomposed as DS, where D is a diagonal matrix
Diagonal matrix
In linear algebra, a diagonal matrix is a matrix in which the entries outside the main diagonal are all zero. The diagonal entries themselves may or may not be zero...
with positive integer entries and S is a symmetric matrix. Under the assumptions that C is symmetrizable and indecomposable, the Kac–Moody algebras are divided into three classes:
- A positive definite matrix S gives rise to a finite-dimensional simple Lie algebra.
- A positive semidefinite matrix S gives rise to an infinite-dimensional Kac–Moody algebra of affine type, or an affine Lie algebraAffine Lie algebraIn mathematics, an affine Lie algebra is an infinite-dimensional Lie algebra that is constructed in a canonical fashion out of a finite-dimensional simple Lie algebra. It is a Kac–Moody algebra for which the generalized Cartan matrix is positive semi-definite and has corank 1...
. - An indefinite matrix S gives rise to a Kac–Moody algebra of indefinite type.
- Since the diagonal entries of C and S are positive, S cannot be negative definite or negative semidefinite.
Symmetrizable indecomposable generalized Cartan matrices of finite and affine type have been completely classified. They correspond to Dynkin diagrams and affine Dynkin diagrams. Very little is known about the Kac–Moody algebras of indefinite type. Among those, the main focus has been on the (generalized) Kac–Moody algebras of hyperbolic type, for which the matrix S is indefinite, but for each proper subset of I, the corresponding submatrix is positive definite or positive semidefinite. Such matrices have rank at most 10 and have also been completely determined.
See also
- Weyl–Kac character formula
- Generalized Kac–Moody algebraGeneralized Kac–Moody algebraIn mathematics, a generalized Kac–Moody algebra is a Lie algebra that is similar to aKac–Moody algebra, except that it is allowed to have imaginary simple roots.Generalized Kac–Moody algebras are also sometimes called GKM algebras,...
In mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a Kac–Moody algebra (named for Victor Kac
Victor Kac
Victor G. Kac is a Soviet and American mathematician at MIT, known for his work in representation theory. He discovered Kac–Moody algebras, and used the Weyl–Kac character formula for them to reprove the Macdonald identities...
and Robert Moody
Robert Moody
Robert Vaughan Moody, OC, FRSC is a Canadian mathematician. He is the co-discover of Kac-Moody algebra, a Lie algebra, usually infinite-dimensional, that can be defined through a generalized root system....
, who independently discovered them) is a Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
, usually infinite-dimensional, that can be defined by generators and relations through a generalized Cartan matrix. These algebras form a generalization of finite-dimensional semisimple Lie algebras, and many properties related to the structure of a Lie algebra such as its root system
Root system
In mathematics, a root system is a configuration of vectors in a Euclidean space satisfying certain geometrical properties. The concept is fundamental in the theory of Lie groups and Lie algebras...
, irreducible representations
Representation of a Lie algebra
In the mathematical field of representation theory, a Lie algebra representation or representation of a Lie algebra is a way of writing a Lie algebra as a set of matrices in such a way that the Lie bracket is given by the commutator.The notion is closely related to that of a representation of a...
, and connection to flag manifold
Flag manifold
In mathematics, a generalized flag variety is a homogeneous space whose points are flags in a finite-dimensional vector space V over a field F. When F is the real or complex numbers, a generalized flag variety is a smooth or complex manifold, called a real or complex flag manifold...
s have natural analogues in the Kac–Moody setting.
A class of Kac–Moody algebras called affine Lie algebra
Affine Lie algebra
In mathematics, an affine Lie algebra is an infinite-dimensional Lie algebra that is constructed in a canonical fashion out of a finite-dimensional simple Lie algebra. It is a Kac–Moody algebra for which the generalized Cartan matrix is positive semi-definite and has corank 1...
s is of particular importance in mathematics and theoretical physics
Theoretical physics
Theoretical physics is a branch of physics which employs mathematical models and abstractions of physics to rationalize, explain and predict natural phenomena...
, especially conformal field theory
Conformal field theory
A conformal field theory is a quantum field theory that is invariant under conformal transformations...
and the theory of exactly solvable models. Kac discovered an elegant proof of certain combinatorial identities, Macdonald
Ian G. Macdonald
Ian Grant Macdonald is a British mathematician known for his contributions to symmetric functions, special functions, Lie algebra theory and other aspects of algebraic combinatorics ....
identities
Macdonald identities
In mathematics, the Macdonald identities are some infinite product identities associated to affine root systems, introduced by . They include as special cases the Jacobi triple product identity, Watson's quintuple product identity, several identities found by , and a 10-fold product identity found...
, which is based on the representation theory of affine Kac–Moody algebras. Howard Garland and James Lepowsky
James Lepowsky
James Lepowsky is a professor of mathematics at Rutgers University, New Jersey. Previously he taught at Yale University. He received his Ph.D from M.I.T. in 1970 where his advisor was Bertram Kostant. Lepowsky graduated from Stuyvesant High School in 1961, 16 years after Kostant...
demonstrated that Rogers-Ramanujan identities
Rogers-Ramanujan identities
In mathematics, the Rogers–Ramanujan identities are two identities related to basic hypergeometric series, first discovered and proved by . They were subsequently rediscovered by Srinivasa Ramanujan some time before 1913. Ramanujan had no proof, but rediscovered Rogers's paper in 1917, and they...
can be derived in a similar fashion.
History of Kac-Moody algebras
The initial construction by Élie CartanÉlie Cartan
Élie Joseph Cartan was an influential French mathematician, who did fundamental work in the theory of Lie groups and their geometric applications...
and Wilhelm Killing
Wilhelm Killing
Wilhelm Karl Joseph Killing was a German mathematician who made important contributions to the theories of Lie algebras, Lie groups, and non-Euclidean geometry....
of finite dimensional simple Lie algebras from the Cartan integers was type dependent. In 1966 Jean-Pierre Serre
Jean-Pierre Serre
Jean-Pierre Serre is a French mathematician. He has made contributions in the fields of algebraic geometry, number theory, and topology.-Early years:...
showed that relations of Claude Chevalley
Claude Chevalley
Claude Chevalley was a French mathematician who made important contributions to number theory, algebraic geometry, class field theory, finite group theory, and the theory of algebraic groups...
and Harish-Chandra
Harish-Chandra
Harish-Chandra was an Indian mathematician, who did fundamental work in representation theory, especially Harmonic analysis on semisimple Lie groups. -Life:...
, with simplifications by Nathan Jacobson
Nathan Jacobson
Nathan Jacobson was an American mathematician....
, give a defining presentation for the Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
. One could thus describe a simple Lie algebra in terms of generators and relations using data from the matrix of Cartan integers, which is naturally positive definite.
In his 1967 thesis, Robert Moody
Robert Moody
Robert Vaughan Moody, OC, FRSC is a Canadian mathematician. He is the co-discover of Kac-Moody algebra, a Lie algebra, usually infinite-dimensional, that can be defined through a generalized root system....
considered Lie algebras whose Cartan matrix
Cartan matrix
In mathematics, the term Cartan matrix has three meanings. All of these are named after the French mathematician Élie Cartan. In fact, Cartan matrices in the context of Lie algebras were first investigated by Wilhelm Killing, whereas the Killing form is due to Cartan.- Lie algebras :A generalized...
is no longer positive definite. This still gave rise to a Lie algebra, but one which is now infinite dimensional. Simultaneously, Z-graded Lie algebra
Graded Lie algebra
In mathematics, a graded Lie algebra is a Lie algebra endowed with a gradation which is compatible with the Lie bracket. In other words, a graded Lie algebra is a Lie algebra which is also a nonassociative graded algebra under the bracket operation. A choice of Cartan decomposition endows any...
s were being studied in Moscow where I. L. Kantor introduced and studied a general class of Lie algebras including what eventually became known as Kac–Moody algebras. Victor Kac
Victor Kac
Victor G. Kac is a Soviet and American mathematician at MIT, known for his work in representation theory. He discovered Kac–Moody algebras, and used the Weyl–Kac character formula for them to reprove the Macdonald identities...
was also studying simple or nearly simple Lie algebras with polynomial growth. A rich mathematical theory of infinite dimensional Lie algebras evolved. An account of the subject, which also includes works of many others is given in (Kac 1990). See also (Seligman 1987).
Definition
A Kac–Moody algebra is given by the following:- An n×n generalized Cartan matrix of rankRank (linear algebra)The column rank of a matrix A is the maximum number of linearly independent column vectors of A. The row rank of a matrix A is the maximum number of linearly independent row vectors of A...
r. - A vector spaceVector spaceA vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
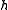 over the complex numberComplex numberA complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
over the complex numberComplex numberA complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s of dimension 2n − r. - A set of n linearly independent elements
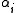 of
of 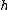 and a set of n linearly independent elements
and a set of n linearly independent elements 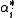 of the dual spaceDual spaceIn mathematics, any vector space, V, has a corresponding dual vector space consisting of all linear functionals on V. Dual vector spaces defined on finite-dimensional vector spaces can be used for defining tensors which are studied in tensor algebra...
of the dual spaceDual spaceIn mathematics, any vector space, V, has a corresponding dual vector space consisting of all linear functionals on V. Dual vector spaces defined on finite-dimensional vector spaces can be used for defining tensors which are studied in tensor algebra...
, such that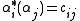 . The
. The 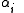 are known as coroots, while the
are known as coroots, while the 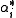 are known as roots.
are known as roots.
The Kac–Moody algebra is the Lie algebra
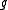 defined by generators
defined by generatorsGenerating set
In mathematics, the expressions generator, generate, generated by and generating set can have several closely related technical meanings:...
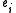 and
and 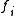 and the elements of
and the elements of 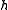 and relations
and relations
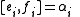
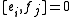 for
for 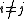
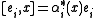 , for
, for 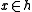
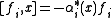 , for
, for 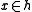
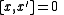 for
for 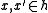
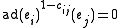
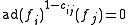
where
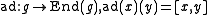 is the adjoint representation of
is the adjoint representation of 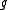 .
.A real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
(possibly infinite-dimensional) Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
is also considered a Kac–Moody algebra if its complexification
Complexification
In mathematics, the complexification of a real vector space V is a vector space VC over the complex number field obtained by formally extending scalar multiplication to include multiplication by complex numbers. Any basis for V over the real numbers serves as a basis for VC over the complex...
is a Kac–Moody algebra.
Interpretation
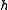 is a Cartan subalgebra of the Kac–Moody algebra.
is a Cartan subalgebra of the Kac–Moody algebra.If g is an element of the Kac–Moody algebra such that
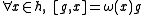
where ω is an element of
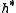 , then g is said to have weight ω. The Kac–Moody algebra can be diagonalized into weight eigenvectors. The Cartan subalgebra h has weight zero, ei has weight α*i and fi has weight −α*i. If the Lie bracket
, then g is said to have weight ω. The Kac–Moody algebra can be diagonalized into weight eigenvectors. The Cartan subalgebra h has weight zero, ei has weight α*i and fi has weight −α*i. If the Lie bracketLie bracket of vector fields
In the mathematical field of differential topology, the Lie bracket of vector fields, Jacobi–Lie bracket, or commutator of vector fields is a bilinear differential operator which assigns, to any two vector fields X and Y on a smooth manifold M, a third vector field denoted [X, Y]...
of two weight eigenvectors is nonzero, then its weight is the sum of their weights. The condition
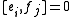 for
for 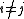 simply means the α*i are simple root
simply means the α*i are simple rootSimple root
in mathematics the term simple root can refer to one of two unrelated notions:*A simple root of a polynomial is a root of multiplicity one*A simple root in a root system is a member of a subset determined by a choice of positive roots...
s.
Types of Kac–Moody algebras
Properties of a Kac–Moody algebra are controlled by the algebraic properties of its generalized Cartan matrix C. In order to classify Kac–Moody algebras, it is enough to consider the case of an indecomposable matrixC, that is, assume that there is no decomposition of the set of indices I into a disjoint union of non-empty subsets I1 and I2 such that Cij = 0 for all i in I1 and j in I2. Any decomposition of the generalized Cartan matrix leads to the direct sum decomposition of the corresponding Kac–Moody algebra:where the two Kac–Moody algebras in the right hand side are associated with the submatrices of C corresponding to the index sets I1 and I2.
An important subclass of Kac–Moody algebras corresponds to symmetrizable generalized Cartan matrices C, which can be decomposed as DS, where D is a diagonal matrix
Diagonal matrix
In linear algebra, a diagonal matrix is a matrix in which the entries outside the main diagonal are all zero. The diagonal entries themselves may or may not be zero...
with positive integer entries and S is a symmetric matrix. Under the assumptions that C is symmetrizable and indecomposable, the Kac–Moody algebras are divided into three classes:
- A positive definite matrix S gives rise to a finite-dimensional simple Lie algebra.
- A positive semidefinite matrix S gives rise to an infinite-dimensional Kac–Moody algebra of affine type, or an affine Lie algebraAffine Lie algebraIn mathematics, an affine Lie algebra is an infinite-dimensional Lie algebra that is constructed in a canonical fashion out of a finite-dimensional simple Lie algebra. It is a Kac–Moody algebra for which the generalized Cartan matrix is positive semi-definite and has corank 1...
. - An indefinite matrix S gives rise to a Kac–Moody algebra of indefinite type.
- Since the diagonal entries of C and S are positive, S cannot be negative definite or negative semidefinite.
Symmetrizable indecomposable generalized Cartan matrices of finite and affine type have been completely classified. They correspond to Dynkin diagrams and affine Dynkin diagrams. Very little is known about the Kac–Moody algebras of indefinite type. Among those, the main focus has been on the (generalized) Kac–Moody algebras of hyperbolic type, for which the matrix S is indefinite, but for each proper subset of I, the corresponding submatrix is positive definite or positive semidefinite. Such matrices have rank at most 10 and have also been completely determined.