
Semisimple Lie algebra
Encyclopedia
In mathematics
, a Lie algebra
is semisimple if it is a direct sum
of simple Lie algebras, i.e., non-abelian Lie algebras whose only ideals are {0} and
whose only ideals are {0} and  itself.
itself.
Throughout the article, unless otherwise stated,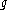 is a finite-dimensional Lie algebra over a field of characteristic 0. The following conditions are equivalent:
is a finite-dimensional Lie algebra over a field of characteristic 0. The following conditions are equivalent:
These Lie algebras are numbered so that n is the rank. Except certain exceptions in low dimensions, many of these are simple Lie algebras, which are a fortiori
semisimple. These four families, together with five exceptions (E6, E7, E8, F4, and G2), are in fact the only simple Lie algebras over the complex numbers.
 Every semisimple Lie algebra over an algebraically closed field is a direct sum
Every semisimple Lie algebra over an algebraically closed field is a direct sum
of simple Lie algebras (by definition), and the simple Lie algebras fall in four families – An, Bn, Cn, and Dn – with five exceptions
E6, E7, E8, F4, and G2. Simple Lie algebras are classified by the connected Dynkin diagrams, shown at right, while semisimple Lie algebras correspond to not necessarily connected Dynkin diagrams, where each component of the diagram corresponds to a summand of the decomposition of the semisimple Lie algebra into simple Lie algebras.
The classification proceeds by considering a Cartan subalgebra (maximal abelian Lie algebra; corresponds to a maximal torus
in a Lie group) and the adjoint action of the Lie algebra on this subalgebra. The root system
of the action then both determines the original Lie algebra and must have a very constrained form, which can be classified by the Dynkin diagrams.
The classification is widely considered one of the most elegant results in mathematics – a brief list of axioms yields, via a relatively short proof, a complete but non-trivial classification with surprising structure. This should be compared to the classification of finite simple groups
, which is significantly more complicated.
The enumeration of the four families is non-redundant and consists only of simple algebras if for An,
for An, 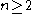 for Bn,
for Bn, 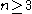 for Cn, and
for Cn, and  for Dn. If one starts numbering lower, the enumeration is redundant, and one has exceptional isomorphism
for Dn. If one starts numbering lower, the enumeration is redundant, and one has exceptional isomorphism
s between simple Lie algebras, which are reflected in isomorphisms of Dynkin diagrams; the En can also be extended down, but below E6 are isomorphic to other, non-exceptional algebras.
Over a non-algebraically closed field, the classification is more complicated – one classifies simple Lie algebras over the algebraic closure, then for each of these, one classifies simple Lie algebras over the original field which have this form (over the closure). For example, to classify simple real Lie algebras, one classifies real Lie algebras with a given complexification, which are known as real forms
of the complex Lie algebra; this can be done by Satake diagram
s, which are Dynkin diagrams with addition data ("decorations").
(1888–90), though his proof lacked rigor. His proof was made rigorous by Élie Cartan
(1894) in his Ph.D. thesis, who also classified semisimple real Lie algebras. This was subsequently refined, and the present classification by Dynkin diagrams was given by then 22-year old Eugene Dynkin
in 1947. Some minor modifications have been made (notably by J. P. Serre), but the proof is unchanged in its essentials and can be found in any standard reference, such as .
: every finite-dimensional representation
is completely reducible; that is for every invariant subspace of the representation there is an invariant complement. Infinite-dimensional representations of semisimple Lie algebras are not in general completely reducible.
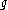 is an abelian ideal, if
is an abelian ideal, if  is semisimple, then its center is zero. (Note: since
is semisimple, then its center is zero. (Note: since 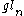 has non-trivial center, it is not semisimple.) In other words, the adjoint representation
has non-trivial center, it is not semisimple.) In other words, the adjoint representation 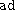 is injective. Moreover, it can be shown that the dimension of the Lie algebra
is injective. Moreover, it can be shown that the dimension of the Lie algebra  of derivations
of derivations
on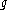 is equal to the dimension of
is equal to the dimension of  . Hence,
. Hence, 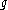 is Lie algebra isomorphic to
is Lie algebra isomorphic to  . Every ideal, quotient and product of semisimple Lie algebras is again semisimple.
. Every ideal, quotient and product of semisimple Lie algebras is again semisimple.
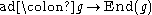 is injective, and so a semisimple Lie algebra is also a linear Lie algebra under the adjoint representation. This may lead to some ambiguity, as every Lie algebra is already linear with respect to some other vector space (Ado's theorem
is injective, and so a semisimple Lie algebra is also a linear Lie algebra under the adjoint representation. This may lead to some ambiguity, as every Lie algebra is already linear with respect to some other vector space (Ado's theorem
), although not necessarily via the adjoint representation. But in practice, such ambiguity rarely occurs.

such that s and n commute with each other. Moreover, each of s and n is a polynomial in x. This is a consequence of the Jordan decomposition
.
If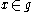 , then the image of x under the adjoint map decomposes as
, then the image of x under the adjoint map decomposes as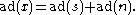
The elements s and n are unique elements of such that n is nilpotent and s is semisimple for which such a decomposition holds. This abstract Jordan decomposition factors through any representation of
such that n is nilpotent and s is semisimple for which such a decomposition holds. This abstract Jordan decomposition factors through any representation of  in the sense that given any representation ρ,
in the sense that given any representation ρ,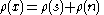
is the Jordan decomposition of ρ(x) in the endomorphism ring of the representation space.
, which states that every finite dimensional Lie algebra is the semidirect product of a solvable ideal (its radical) and a semisimple algebra. In particular, there is no nonzero Lie algebra that is both solvable and semisimple.
Semisimple Lie algebras have a very elegant classification, in stark contrast to solvable Lie algebras. Semisimple Lie algebras over an algebraically closed field are completely classified by their root system
, which are in turn classified by Dynkin diagrams. Semisimple algebras over non-algebraically closed fields can be understood in terms of those over the algebraic closure, though the classification is somewhat more intricate; see real form for the case of real semisimple Lie algebras, which were classified by Élie Cartan
.
Further, the representation theory of semisimple Lie algebras is much cleaner than that for general Lie algebras. For example, the Jordan decomposition in a semisimple Lie algebra coincides with the Jordan decomposition in its representation; this is not the case for Lie algebras in general.
If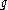 is semisimple, then
is semisimple, then 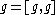 . In particular, every linear semisimple Lie algebra is a subalgebra of
. In particular, every linear semisimple Lie algebra is a subalgebra of 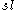 , the special linear Lie algebra
, the special linear Lie algebra
. The study of the structure of constitutes an important part of the representation theory for semisimple Lie algebras.
constitutes an important part of the representation theory for semisimple Lie algebras.
 is semisimple, and
is semisimple, and  is reductive. Many properties of semisimple Lie algebras depend only on reducibility.
is reductive. Many properties of semisimple Lie algebras depend only on reducibility.
Many properties of complex semisimple/reductive Lie algebras are true not only for semisimple/reductive Lie algebras over algebraically closed fields, but more generally for split semisimple/reductive Lie algebras over other fields: semisimple/reductive Lie algebras over algebraically closed fields are always split, but over other fields this is not always the case. Split Lie algebras have essentially the same representation theory as semsimple Lie algebras over algebraically closed fields, for instance, the splitting Cartan subalgebra playing the same role as the Cartan subalgebra plays over algebraically closed fields. This is the approach followed in , for instance, which classifies representations of split semisimple/reductive Lie algebras.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
is semisimple if it is a direct sum
Direct sum of modules
In abstract algebra, the direct sum is a construction which combines several modules into a new, larger module. The result of the direct summation of modules is the "smallest general" module which contains the given modules as submodules...
of simple Lie algebras, i.e., non-abelian Lie algebras
 whose only ideals are {0} and
whose only ideals are {0} and  itself.
itself.Throughout the article, unless otherwise stated,
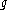 is a finite-dimensional Lie algebra over a field of characteristic 0. The following conditions are equivalent:
is a finite-dimensional Lie algebra over a field of characteristic 0. The following conditions are equivalent:
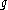 is semisimple
is semisimple- the Killing formKilling formIn mathematics, the Killing form, named after Wilhelm Killing, is a symmetric bilinear form that plays a basic role in the theories of Lie groups and Lie algebras...
, κ(x,y) = tr(ad(x)ad(y)), is non-degenerate, 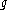 has no non-zero abelian ideals,
has no non-zero abelian ideals,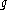 has no non-zero solvable ideals,
has no non-zero solvable ideals,- The radical of
 is zero.
is zero.
Examples
Examples of semisimple Lie algebras, with notation coming from classification by Dynkin diagrams, are:-
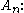
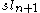 , the special linear Lie algebraSpecial linear Lie algebraIn mathematics, the special linear Lie algebra of order n is the Lie algebra of n \times n matrices with trace zero and with the Lie bracket [X,Y]:=XY-YX...
, the special linear Lie algebraSpecial linear Lie algebraIn mathematics, the special linear Lie algebra of order n is the Lie algebra of n \times n matrices with trace zero and with the Lie bracket [X,Y]:=XY-YX...
. -
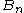
 , the odd-dimensional special orthogonal Lie algebra.
, the odd-dimensional special orthogonal Lie algebra. -

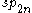 , the symplectic Lie algebra.
, the symplectic Lie algebra. -
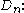
 , the even-dimensional special orthogonal Lie algebra.
, the even-dimensional special orthogonal Lie algebra.
These Lie algebras are numbered so that n is the rank. Except certain exceptions in low dimensions, many of these are simple Lie algebras, which are a fortiori
A fortiori argument
The Latin phrase ' denotes "argument 'from [the] stronger [reason]'." For example, if it has been established that a person is deceased, then one can, with equal or greater certainty, argue that the person is not breathing.-Usage:...
semisimple. These four families, together with five exceptions (E6, E7, E8, F4, and G2), are in fact the only simple Lie algebras over the complex numbers.
Classification

Direct sum
In mathematics, one can often define a direct sum of objectsalready known, giving a new one. This is generally the Cartesian product of the underlying sets , together with a suitably defined structure. More abstractly, the direct sum is often, but not always, the coproduct in the category in question...
of simple Lie algebras (by definition), and the simple Lie algebras fall in four families – An, Bn, Cn, and Dn – with five exceptions
E6, E7, E8, F4, and G2. Simple Lie algebras are classified by the connected Dynkin diagrams, shown at right, while semisimple Lie algebras correspond to not necessarily connected Dynkin diagrams, where each component of the diagram corresponds to a summand of the decomposition of the semisimple Lie algebra into simple Lie algebras.
The classification proceeds by considering a Cartan subalgebra (maximal abelian Lie algebra; corresponds to a maximal torus
Maximal torus
In the mathematical theory of compact Lie groups a special role is played by torus subgroups, in particular by the maximal torus subgroups.A torus in a Lie group G is a compact, connected, abelian Lie subgroup of G . A maximal torus is one which is maximal among such subgroups...
in a Lie group) and the adjoint action of the Lie algebra on this subalgebra. The root system
Root system
In mathematics, a root system is a configuration of vectors in a Euclidean space satisfying certain geometrical properties. The concept is fundamental in the theory of Lie groups and Lie algebras...
of the action then both determines the original Lie algebra and must have a very constrained form, which can be classified by the Dynkin diagrams.
The classification is widely considered one of the most elegant results in mathematics – a brief list of axioms yields, via a relatively short proof, a complete but non-trivial classification with surprising structure. This should be compared to the classification of finite simple groups
Classification of finite simple groups
In mathematics, the classification of the finite simple groups is a theorem stating that every finite simple group belongs to one of four categories described below. These groups can be seen as the basic building blocks of all finite groups, in much the same way as the prime numbers are the basic...
, which is significantly more complicated.
The enumeration of the four families is non-redundant and consists only of simple algebras if
 for An,
for An, 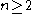 for Bn,
for Bn, 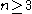 for Cn, and
for Cn, and  for Dn. If one starts numbering lower, the enumeration is redundant, and one has exceptional isomorphism
for Dn. If one starts numbering lower, the enumeration is redundant, and one has exceptional isomorphismExceptional isomorphism
In mathematics, an exceptional isomorphism, also called an accidental isomorphism, is an isomorphism between members ai and bj of two families of mathematical objects, that is not an example of a pattern of such isomorphisms.Because these series of objects are presented differently, they are not...
s between simple Lie algebras, which are reflected in isomorphisms of Dynkin diagrams; the En can also be extended down, but below E6 are isomorphic to other, non-exceptional algebras.
Over a non-algebraically closed field, the classification is more complicated – one classifies simple Lie algebras over the algebraic closure, then for each of these, one classifies simple Lie algebras over the original field which have this form (over the closure). For example, to classify simple real Lie algebras, one classifies real Lie algebras with a given complexification, which are known as real forms
Real form (Lie theory)
In mathematics, the notion of a real form relates objects defined over the field of real and complex numbers. A real Lie algebra g0 is called a real form of a complex Lie algebra g if g is the complexification of g0:...
of the complex Lie algebra; this can be done by Satake diagram
Satake diagram
In the mathematical study of Lie algebras and Lie groups, a Satake diagram is a generalization of a Dynkin diagram whose configurations classify simple Lie algebras over the field of real numbers...
s, which are Dynkin diagrams with addition data ("decorations").
History
The semisimple Lie algebras over the complex numbers were first classified by Wilhelm KillingWilhelm Killing
Wilhelm Karl Joseph Killing was a German mathematician who made important contributions to the theories of Lie algebras, Lie groups, and non-Euclidean geometry....
(1888–90), though his proof lacked rigor. His proof was made rigorous by Élie Cartan
Élie Cartan
Élie Joseph Cartan was an influential French mathematician, who did fundamental work in the theory of Lie groups and their geometric applications...
(1894) in his Ph.D. thesis, who also classified semisimple real Lie algebras. This was subsequently refined, and the present classification by Dynkin diagrams was given by then 22-year old Eugene Dynkin
Eugene Dynkin
Eugene Borisovich Dynkin is a Soviet and American mathematician. He has made contributions to the fields of probability and algebra, especially semisimple Lie groups, Lie algebras, and Markov processes...
in 1947. Some minor modifications have been made (notably by J. P. Serre), but the proof is unchanged in its essentials and can be found in any standard reference, such as .
Complete reducibility
A consequence of semisimplicity is a theorem due to WeylUnitarian trick
In mathematics, the unitarian trick is a device in the representation theory of Lie groups, introduced by for the special linear group and by Hermann Weyl for general semisimple groups. It applies to show that the representation theory of some group G is in a qualitative way controlled by that...
: every finite-dimensional representation
Representation of a Lie algebra
In the mathematical field of representation theory, a Lie algebra representation or representation of a Lie algebra is a way of writing a Lie algebra as a set of matrices in such a way that the Lie bracket is given by the commutator.The notion is closely related to that of a representation of a...
is completely reducible; that is for every invariant subspace of the representation there is an invariant complement. Infinite-dimensional representations of semisimple Lie algebras are not in general completely reducible.
Centerless
Since the center of a Lie algebra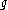 is an abelian ideal, if
is an abelian ideal, if  is semisimple, then its center is zero. (Note: since
is semisimple, then its center is zero. (Note: since 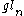 has non-trivial center, it is not semisimple.) In other words, the adjoint representation
has non-trivial center, it is not semisimple.) In other words, the adjoint representation 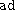 is injective. Moreover, it can be shown that the dimension of the Lie algebra
is injective. Moreover, it can be shown that the dimension of the Lie algebra  of derivations
of derivationsDerivation (abstract algebra)
In abstract algebra, a derivation is a function on an algebra which generalizes certain features of the derivative operator. Specifically, given an algebra A over a ring or a field K, a K-derivation is a K-linear map D: A → A that satisfies Leibniz's law: D = b + a.More...
on
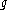 is equal to the dimension of
is equal to the dimension of  . Hence,
. Hence, 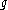 is Lie algebra isomorphic to
is Lie algebra isomorphic to  . Every ideal, quotient and product of semisimple Lie algebras is again semisimple.
. Every ideal, quotient and product of semisimple Lie algebras is again semisimple.Linear
The adjoint representation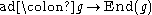 is injective, and so a semisimple Lie algebra is also a linear Lie algebra under the adjoint representation. This may lead to some ambiguity, as every Lie algebra is already linear with respect to some other vector space (Ado's theorem
is injective, and so a semisimple Lie algebra is also a linear Lie algebra under the adjoint representation. This may lead to some ambiguity, as every Lie algebra is already linear with respect to some other vector space (Ado's theoremAdo's theorem
In abstract algebra, Ado's theorem states that every finite-dimensional Lie algebra L over a field K of characteristic zero can be viewed as a Lie algebra of square matrices under the commutator bracket...
), although not necessarily via the adjoint representation. But in practice, such ambiguity rarely occurs.
Jordan decomposition
Any endomorphism x of a finite-dimensional vector space over an algebraically closed field can be decomposed uniquely into a diagonalizable (or semisimple) and nilpotent part
such that s and n commute with each other. Moreover, each of s and n is a polynomial in x. This is a consequence of the Jordan decomposition
Jordan decomposition
In mathematics, Jordan decomposition may refer to* Hahn decomposition theorem, and the Jordan decomposition of a measure* Jordan normal form of a matrix* Jordan–Chevalley decomposition of a matrix...
.
If
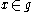 , then the image of x under the adjoint map decomposes as
, then the image of x under the adjoint map decomposes as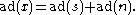
The elements s and n are unique elements of
 such that n is nilpotent and s is semisimple for which such a decomposition holds. This abstract Jordan decomposition factors through any representation of
such that n is nilpotent and s is semisimple for which such a decomposition holds. This abstract Jordan decomposition factors through any representation of  in the sense that given any representation ρ,
in the sense that given any representation ρ,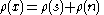
is the Jordan decomposition of ρ(x) in the endomorphism ring of the representation space.
Rank
The rank of a complex semisimple Lie algebra is the dimension of any of its Cartan subalgebras.Significance
The significance of semisimplicity comes firstly from the Levi decompositionLevi decomposition
In Lie theory and representation theory, the Levi decomposition, conjectured by Killing and Cartan and proved by , states that any finite dimensional real Lie algebra g is the semidirect product of a solvable ideal and a semisimple subalgebra....
, which states that every finite dimensional Lie algebra is the semidirect product of a solvable ideal (its radical) and a semisimple algebra. In particular, there is no nonzero Lie algebra that is both solvable and semisimple.
Semisimple Lie algebras have a very elegant classification, in stark contrast to solvable Lie algebras. Semisimple Lie algebras over an algebraically closed field are completely classified by their root system
Root system
In mathematics, a root system is a configuration of vectors in a Euclidean space satisfying certain geometrical properties. The concept is fundamental in the theory of Lie groups and Lie algebras...
, which are in turn classified by Dynkin diagrams. Semisimple algebras over non-algebraically closed fields can be understood in terms of those over the algebraic closure, though the classification is somewhat more intricate; see real form for the case of real semisimple Lie algebras, which were classified by Élie Cartan
Élie Cartan
Élie Joseph Cartan was an influential French mathematician, who did fundamental work in the theory of Lie groups and their geometric applications...
.
Further, the representation theory of semisimple Lie algebras is much cleaner than that for general Lie algebras. For example, the Jordan decomposition in a semisimple Lie algebra coincides with the Jordan decomposition in its representation; this is not the case for Lie algebras in general.
If
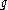 is semisimple, then
is semisimple, then 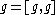 . In particular, every linear semisimple Lie algebra is a subalgebra of
. In particular, every linear semisimple Lie algebra is a subalgebra of 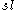 , the special linear Lie algebra
, the special linear Lie algebraSpecial linear Lie algebra
In mathematics, the special linear Lie algebra of order n is the Lie algebra of n \times n matrices with trace zero and with the Lie bracket [X,Y]:=XY-YX...
. The study of the structure of
 constitutes an important part of the representation theory for semisimple Lie algebras.
constitutes an important part of the representation theory for semisimple Lie algebras.Generalizations
Semisimple Lie algebras admit certain generalizations. Firstly, many statements that are true for semisimple Lie algebras are true more generally for reductive Lie algebras. Abstractly, a reductive Lie algebra is one whose adjoint representation is completely reducible, while concretely, a reductive Lie algebra is a direct sum of a semisimple Lie algebra and an abelian Lie algebra; for example, is semisimple, and
is semisimple, and  is reductive. Many properties of semisimple Lie algebras depend only on reducibility.
is reductive. Many properties of semisimple Lie algebras depend only on reducibility.Many properties of complex semisimple/reductive Lie algebras are true not only for semisimple/reductive Lie algebras over algebraically closed fields, but more generally for split semisimple/reductive Lie algebras over other fields: semisimple/reductive Lie algebras over algebraically closed fields are always split, but over other fields this is not always the case. Split Lie algebras have essentially the same representation theory as semsimple Lie algebras over algebraically closed fields, for instance, the splitting Cartan subalgebra playing the same role as the Cartan subalgebra plays over algebraically closed fields. This is the approach followed in , for instance, which classifies representations of split semisimple/reductive Lie algebras.

