Radical of a Lie algebra
Encyclopedia
In the mathematical field of Lie theory
, the radical of a Lie algebra
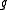is the largest solvable ideal of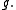 
be a field and let 
be a finite-dimensional Lie algebra
over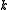
. A maximal solvable ideal, which is called the radical, exists for the following reason.
Firstly let
and 
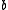be two solvable ideals of 
. Then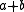 
is again an ideal of 
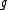, and it is solvable because it is an extension of 
by 
. Therefore we may also define the radical of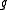 
as the sum of all the solvable ideals of 
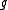, hence the radical of 
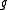is unique. Secondly, as 
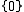is always a solvable ideal of 
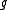, the radical of 
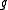always exists.
Lie theory
Lie theory is an area of mathematics, developed initially by Sophus Lie.Early expressions of Lie theory are found in books composed by Lie with Friedrich Engel and Georg Scheffers from 1888 to 1896....
, the radical of a Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
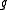is the largest solvable ideal of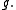 Definition
Let be a field and let be a finite-dimensional Lie algebraLie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
over
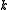. A maximal solvable ideal, which is called the radical, exists for the following reason.Firstly let
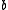and be two solvable ideals of . Then 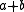is again an ideal of 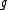, and it is solvable because it is an extension of by . Therefore we may also define the radical of 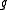as the sum of all the solvable ideals of 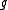, hence the radical of 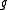is unique. Secondly, as 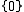is always a solvable ideal of 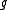, the radical of 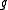always exists.Related concepts
- A Lie algebra is semisimple if and only if its radical is
. - A Lie algebra is reductive if and only if its radical equals its center.