E8 lattice
Encyclopedia
In mathematics
, the E8 lattice is a special lattice
in R8. It can be characterized as the unique positive-definite, even, unimodular lattice
of rank 8. The name derives from the fact that it is the root lattice of the E8 root system
.
The norm of the E8 lattice (divided by 2) is a positive definite even unimodular quadratic form
in 8 variables, and conversely such a quadratic form can be used to construct a positive-definite, even, unimodular lattice
of rank 8.
The existence of such a form was first shown by H. J. S. Smith in 1867, and the first explicit construction of this quadratic form was given by A. Korkine and G. Zolotareff in 1873.
The E8 lattice is also called the Gosset lattice after Thorold Gosset
who was one of the first to study the geometry of the lattice itself around 1900.
In symbols,
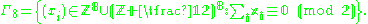
It is not hard to check that the sum of two lattice points is another lattice point, so that Γ8 is indeed a subgroup.
An alternative description of the E8 lattice which is sometimes convenient is the set of all points in Γ′8 ⊂ R8 such that
In symbols,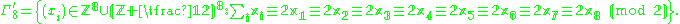
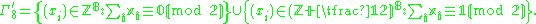
The lattices Γ8 and Γ′8 are isomorphic and one may pass from one to the other by changing the signs of any odd number of coordinates. The lattice Γ8 is sometimes called the even coordinate system for E8 while the lattice Γ8' is called the odd coordinate system. Unless we specify otherwise we shall work in the even coordinate system.
Even unimodular lattices can occur only in dimensions divisible by 8. In dimension 16 there are two such lattices: Γ8 ⊕ Γ8 and Γ16 (constructed in an analogous fashion to Γ8). In dimension 24 there are 24 such lattices, called Niemeier lattice
s. The most important of these is the Leech lattice
.
One possible basis for Γ8 is given by the columns of the (upper triangular) matrix
Γ8 is then the integral span of these vectors. All other possible bases are obtained from this one by right multiplication by elements of GL(8,Z).
The shortest nonzero vectors in Γ8 have norm 2. There are 240 such vectors.
These form a root system
of type E8
. The lattice Γ8 is equal to the E8 root lattice, meaning that it is given by the integral span of the 240 roots. Any choice of 8 simple root
s gives a basis for Γ8.
) of a lattice in Rn is defined as the subgroup of the orthogonal group
O(n) that preserves the lattice. The symmetry group of the E8 lattice is the Weyl
/Coxeter group
of type E8. This is the group generated by reflection
s in the hyperplanes orthogonal to the 240 roots of the lattice. Its order
is given by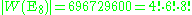
The E8 Weyl group contains a subgroup of order 128·8! consisting of all permutation
s of the coordinates and all even sign changes. This subgroup is the Weyl group of type D8. The full E8 Weyl group is generated by this subgroup and the block diagonal matrix H4⊕H4 where H4 is the Hadamard matrix
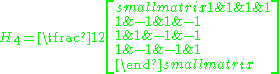
A hole in a lattice is a point in the ambient Euclidean space whose distance to the nearest lattice point is a local maximum. A deep hole is one whose distance to the lattice is a global maximum. There are two types of holes in the E8 lattice:
The E8 lattice points are the vertices of the 521
honeycomb, which is composed of regular 8-simplex and 8-orthoplex facets. This honeycomb was first studied by Gosset who called it a 9-ic semi-regular figure (Gosset regarded honeycombs in n dimensions as degenerate n+1 polytopes). In Coxeter's notation, Gosset's honeycomb is denoted by 521 and has the Coxeter-Dynkin diagram
:
The vertex figure
of Gosset's honeycomb is the semiregular E8 polytope (421 in Coxeter's notation) given by the convex hull
of the 240 roots of the E8 lattice.
Each point of the E8 lattice is surrounded by 2160 8-orthoplexes and 17280 8-simplices. The 2160 deep holes near the origin are exactly the halves of the norm 4 lattice points. The 17520 norm 8 lattice points fall into two classes (two orbits under the action of the E8 automorphism group): 240 are twice the norm 2 lattice points while 17280 are 3 times the shallow holes surrounding the origin.
This honeycomb is highly regular in the sense that its symmetry group (the affine E8 Weyl group) acts transitively on the k-faces
for k ≤ 6. All of the k-faces for k ≤ 7 are simplices.
in 8 dimensions.
The general sphere packing problem asks what is the densest way to pack n-dimensional (solid) spheres in Rn so that no two spheres overlap. Lattice packings are special types of sphere packings where the spheres are centered at the points of a lattice. Placing spheres of radius 1/√2 at the points of the E8 lattice gives a lattice packing in R8 with a density of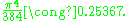
It is known that this is the maximum density that can be achieved by a lattice packing in 8 dimensions. Furthermore, the E8 lattice is the unique lattice (up to isometries and rescalings) with this density. It is conjectured this density is, in fact, optimal (even among irregular packings). Researchers have recently shown that no irregular packing density can exceed that of the E8 lattice by a factor of more than 1 + 10−14.
The kissing number problem asks what is the maximum number of spheres of a fixed radius that can touch (or "kiss") a central sphere of the same radius. In the E8 lattice packing mentioned above any given sphere touches 240 neighboring spheres. This is because there are 240 lattice vectors of minimum nonzero norm (the roots of the E8 lattice). It was shown in 1979 that this is the maximum possible number in 8-dimensions.
The kissing number problem is remarkably difficult and solutions are only known in 1, 2, 3, 4, 8, and 24 dimensions. Perhaps surprisingly, it is easier to find the solution in 8 (and 24) dimensions than in 3 or 4. This follows from the special properties of the E8 lattice (and its 24-dimensional cousin, the Leech lattice
).
The theta function of a lattice is then a holomorphic function
on the upper half-plane. Furthermore, the theta function of an even unimodular lattice of rank n is actually a modular form
of weight n/2. The theta function of an integral lattice is often written as a power series in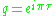
so that the coefficient of qn gives the number of lattice vectors of norm n.
Up to normalization, there is a unique modular form of weight 4: the Eisenstein series
G4(τ). The theta function for the E8 lattice must then be proportional to G4(τ). The normalization can be fixed by noting that there is a unique vector of norm 0. This gives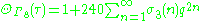
where σ3(n) is the divisor function
. It follows that the number of E8 lattice vectors of norm 2n is 240 times the sum of the cubes of the divisors of n. The first few terms of this series are given by :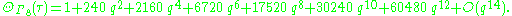
The E8 theta function may be written in terms of the Jacobi theta functions as follows: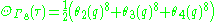
where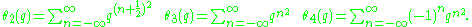
H(8,4) and can, in fact, be constructed from it. The Hamming code H(8,4) is a binary code
of length 8 and rank 4; that is, it is a 4-dimensional subspace of the finite vector space (F2)8. Writing elements of (F2)8 as 8-bit integers in hexadecimal
, the code H(8,4) can by given explicitly as the set
The code H(8,4) is significant partly because it is a Type II self-dual code. It has a minimum Hamming weight
4, meaning that any two codewords differ by at least 4 bits. It is the largest length 8 binary code with this property.
One can construct a lattice Λ from a binary code C of length n by taking the set of all vectors x in Zn such that x is congruent (modulo 2) to a codeword of C. It is often convenient to rescale Λ by a factor of 1/√2,
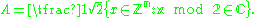
Applying this construction a Type II self-dual code gives an even, unimodular lattice. In particular, applying it to the Hamming code H(8,4) gives an E8 lattice. It is not entirely trivial, however, to find an explicit isomorphism between this lattice and the lattice Γ8 defined above.
s O. It is possible to define the concept of an integral octonion analogous to that of an integral quaternion. The integral octonions naturally form a lattice inside O. This lattice is just a rescaled E8 lattice. (The minimum norm in the integral octonion lattice is 1 rather than 2). Embedded in the octonions in this manner the E8 lattice takes on the structure of a nonassociative ring
.
Fixing a basis (1, i, j, k, ℓ, ℓi, ℓj, ℓk) of unit octonions,
one can define the integral octonions as a maximal order containing this basis. (One must, of course, extend the definitions of order and ring to include the nonassociative case). This amounts to finding the largest subring
of O containing the units on which the expressions x*x (the norm of x) and x + x* (twice the real part of x) are integer-valued. There are actually seven such maximal orders, one corresponding to each of the seven imaginary units. However, all seven maximal orders are isomorphic. One such maximal order is generated by the octonions i, j, and ½ (i + j + k + ℓ).
A detailed account of the integral octonions and their relation to the E8 lattice can be found in Conway and Smith (2003).
1)
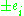, i=0,1,...,7
2)
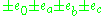, indexes abc span triads: 123, 145, 167, 346, 375, 274, 265
3)
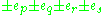, indexes pqrs span fours: 1246, 1257, 1347, 1356, 2345, 2367, 4567
Imaginary octonions in this set (14 from point 1 and 7*16=112 from point 3) form roots of Lie algebra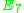
. Adding remaining 2+112 vectors we obtain 240 vectors which form roots of Lie algebra 
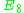. See the Koca work on this subject.
produced a bizarre example of a topological 4-manifold
, called the E8 manifold
, whose intersection form
is given by the E8 lattice. This manifold is an example of a topological manifold which admits no smooth structure
and is not even triangulable
.
In string theory
, the heterotic string
is a peculiar hybrid of a 26-dimensional bosonic string and a 10-dimensional superstring. In order for the theory to work correctly, the 16 mismatched dimensions must be compactified on an even, unimodular lattice of rank 16. There are two such lattices: Γ8⊕Γ8 and Γ16 (constructed in a fashion analogous to that of Γ8). These lead to two version of the heterotic string known as the E8×E8 heterotic string and the SO(32) heterotic string.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the E8 lattice is a special lattice
Lattice (group)
In mathematics, especially in geometry and group theory, a lattice in Rn is a discrete subgroup of Rn which spans the real vector space Rn. Every lattice in Rn can be generated from a basis for the vector space by forming all linear combinations with integer coefficients...
in R8. It can be characterized as the unique positive-definite, even, unimodular lattice
Unimodular lattice
In mathematics, a unimodular lattice is a lattice of determinant 1 or −1.The E8 lattice and the Leech lattice are two famous examples.- Definitions :...
of rank 8. The name derives from the fact that it is the root lattice of the E8 root system
E8 (mathematics)
In mathematics, E8 is any of several closely related exceptional simple Lie groups, linear algebraic groups or Lie algebras of dimension 248; the same notation is used for the corresponding root lattice, which has rank 8...
.
The norm of the E8 lattice (divided by 2) is a positive definite even unimodular quadratic form
Quadratic form
In mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,4x^2 + 2xy - 3y^2\,\!is a quadratic form in the variables x and y....
in 8 variables, and conversely such a quadratic form can be used to construct a positive-definite, even, unimodular lattice
Unimodular lattice
In mathematics, a unimodular lattice is a lattice of determinant 1 or −1.The E8 lattice and the Leech lattice are two famous examples.- Definitions :...
of rank 8.
The existence of such a form was first shown by H. J. S. Smith in 1867, and the first explicit construction of this quadratic form was given by A. Korkine and G. Zolotareff in 1873.
The E8 lattice is also called the Gosset lattice after Thorold Gosset
Thorold Gosset
Thorold Gosset was an English lawyer and an amateur mathematician. In mathematics, he is noted for discovering and classifying the semiregular polytopes in dimensions four and higher.According to H. S. M...
who was one of the first to study the geometry of the lattice itself around 1900.
Lattice points
The E8 lattice is a discrete subgroup of R8 of full rank (i.e. it spans all of R8). It can be given explicitly by the set of points Γ8 ⊂ R8 such that- all the coordinates are integerIntegerThe integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s or all the coordinates are half-integerHalf-integerIn mathematics, a half-integer is a number of the formn + 1/2,where n is an integer. For example,are all half-integers. Note that a half of an integer is not always a half-integer: half of an even integer is an integer but not a half-integer...
s (a mixture of integers and half-integers is not allowed), and - the sum of the eight coordinates is an even integer.
In symbols,
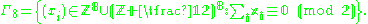
It is not hard to check that the sum of two lattice points is another lattice point, so that Γ8 is indeed a subgroup.
An alternative description of the E8 lattice which is sometimes convenient is the set of all points in Γ′8 ⊂ R8 such that
- all the coordinates are integers and the sum of the coordinates is even, or
- all the coordinates are half-integers and the sum of the coordinates is odd.
In symbols,
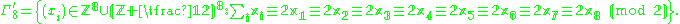
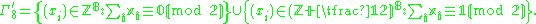
The lattices Γ8 and Γ′8 are isomorphic and one may pass from one to the other by changing the signs of any odd number of coordinates. The lattice Γ8 is sometimes called the even coordinate system for E8 while the lattice Γ8' is called the odd coordinate system. Unless we specify otherwise we shall work in the even coordinate system.
Properties
The E8 lattice Γ8 can be characterized as the unique lattice in R8 with the following properties:- It is unimodularUnimodular latticeIn mathematics, a unimodular lattice is a lattice of determinant 1 or −1.The E8 lattice and the Leech lattice are two famous examples.- Definitions :...
, meaning that it can be generated by the columns of a 8×8 matrix with determinantDeterminantIn linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
±1 (i.e. the volume of the fundamental parallelotope of the lattice is 1). Equivalently, Γ8 is self-dual, meaning it is equal to its dual lattice. - It is even, meaning that the norm of any lattice vector is even.
Even unimodular lattices can occur only in dimensions divisible by 8. In dimension 16 there are two such lattices: Γ8 ⊕ Γ8 and Γ16 (constructed in an analogous fashion to Γ8). In dimension 24 there are 24 such lattices, called Niemeier lattice
Niemeier lattice
In mathematics, a Niemeier lattice is one of the 24positive definite even unimodular lattices of rank 24,which were classified by . gave a simplified proof of the classification. has a sentence mentioning that he found more than 10 such lattices, but gives no further details...
s. The most important of these is the Leech lattice
Leech lattice
In mathematics, the Leech lattice is an even unimodular lattice Λ24 in 24-dimensional Euclidean space E24 found by .-History:Many of the cross-sections of the Leech lattice, including the Coxeter–Todd lattice and Barnes–Wall lattice, in 12 and 16 dimensions, were found much earlier than...
.
One possible basis for Γ8 is given by the columns of the (upper triangular) matrix
Γ8 is then the integral span of these vectors. All other possible bases are obtained from this one by right multiplication by elements of GL(8,Z).
The shortest nonzero vectors in Γ8 have norm 2. There are 240 such vectors.
- All half-integer: (can only be ±1/2)
- All positive or all negative: 2
- Four positive, four negative: (8*7*6*5)/(4*3*2*1)=70
- Two of one, six of the other: 2*(8*7)/(2*1) = 56
- All integer: (can only be 0, ±1)
- Two ±1, six zeroes: 4*(8*7)/(2*1)=112
These form a root system
Root system
In mathematics, a root system is a configuration of vectors in a Euclidean space satisfying certain geometrical properties. The concept is fundamental in the theory of Lie groups and Lie algebras...
of type E8
E8 (mathematics)
In mathematics, E8 is any of several closely related exceptional simple Lie groups, linear algebraic groups or Lie algebras of dimension 248; the same notation is used for the corresponding root lattice, which has rank 8...
. The lattice Γ8 is equal to the E8 root lattice, meaning that it is given by the integral span of the 240 roots. Any choice of 8 simple root
Simple root
in mathematics the term simple root can refer to one of two unrelated notions:*A simple root of a polynomial is a root of multiplicity one*A simple root in a root system is a member of a subset determined by a choice of positive roots...
s gives a basis for Γ8.
Symmetry group
The automorphism group (or symmetry groupSymmetry group
The symmetry group of an object is the group of all isometries under which it is invariant with composition as the operation...
) of a lattice in Rn is defined as the subgroup of the orthogonal group
Orthogonal group
In mathematics, the orthogonal group of degree n over a field F is the group of n × n orthogonal matrices with entries from F, with the group operation of matrix multiplication...
O(n) that preserves the lattice. The symmetry group of the E8 lattice is the Weyl
Weyl group
In mathematics, in particular the theory of Lie algebras, the Weyl group of a root system Φ is a subgroup of the isometry group of the root system. Specifically, it is the subgroup which is generated by reflections through the hyperplanes orthogonal to the roots, and as such is a finite reflection...
/Coxeter group
Coxeter group
In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example...
of type E8. This is the group generated by reflection
Reflection (mathematics)
In mathematics, a reflection is a mapping from a Euclidean space to itself that is an isometry with a hyperplane as set of fixed points; this set is called the axis or plane of reflection. The image of a figure by a reflection is its mirror image in the axis or plane of reflection...
s in the hyperplanes orthogonal to the 240 roots of the lattice. Its order
Order (group theory)
In group theory, a branch of mathematics, the term order is used in two closely related senses:* The order of a group is its cardinality, i.e., the number of its elements....
is given by
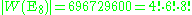
The E8 Weyl group contains a subgroup of order 128·8! consisting of all permutation
Permutation
In mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
s of the coordinates and all even sign changes. This subgroup is the Weyl group of type D8. The full E8 Weyl group is generated by this subgroup and the block diagonal matrix H4⊕H4 where H4 is the Hadamard matrix
Hadamard matrix
In mathematics, an Hadamard matrix, named after the French mathematician Jacques Hadamard, is a square matrix whose entries are either +1 or −1 and whose rows are mutually orthogonal...
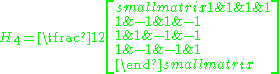
Geometry
- See 521 honeycomb5 21 honeycombIn geometry, the 521 honeycomb is a uniform tessellation of 8-dimensional Euclidean space.This honeycomb was first studied by Gosset who called it a 9-ic semi-regular figure...
A hole in a lattice is a point in the ambient Euclidean space whose distance to the nearest lattice point is a local maximum. A deep hole is one whose distance to the lattice is a global maximum. There are two types of holes in the E8 lattice:
- Deep holes such as the point (1,0,0,0,0,0,0,0) are at a distance of 1 from the nearest lattice points. There are 16 lattice points at this distance which form the vertices of an 8-orthoplex centered at the hole (the Delaunay cell of the hole).
- Shallow holes such as the point
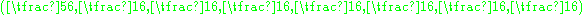are at a distance of 
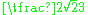from the nearest lattice points. There are 9 lattice points at this distance forming the vertices of an 8-simplex centered at the hole.
The E8 lattice points are the vertices of the 521
5 21 honeycomb
In geometry, the 521 honeycomb is a uniform tessellation of 8-dimensional Euclidean space.This honeycomb was first studied by Gosset who called it a 9-ic semi-regular figure...
honeycomb, which is composed of regular 8-simplex and 8-orthoplex facets. This honeycomb was first studied by Gosset who called it a 9-ic semi-regular figure (Gosset regarded honeycombs in n dimensions as degenerate n+1 polytopes). In Coxeter's notation, Gosset's honeycomb is denoted by 521 and has the Coxeter-Dynkin diagram
Coxeter-Dynkin diagram
In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors...
:
The vertex figure
Vertex figure
In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:...
of Gosset's honeycomb is the semiregular E8 polytope (421 in Coxeter's notation) given by the convex hull
Convex hull
In mathematics, the convex hull or convex envelope for a set of points X in a real vector space V is the minimal convex set containing X....
of the 240 roots of the E8 lattice.
Each point of the E8 lattice is surrounded by 2160 8-orthoplexes and 17280 8-simplices. The 2160 deep holes near the origin are exactly the halves of the norm 4 lattice points. The 17520 norm 8 lattice points fall into two classes (two orbits under the action of the E8 automorphism group): 240 are twice the norm 2 lattice points while 17280 are 3 times the shallow holes surrounding the origin.
This honeycomb is highly regular in the sense that its symmetry group (the affine E8 Weyl group) acts transitively on the k-faces
Face (geometry)
In geometry, a face of a polyhedron is any of the polygons that make up its boundaries. For example, any of the squares that bound a cube is a face of the cube...
for k ≤ 6. All of the k-faces for k ≤ 7 are simplices.
Sphere packings and kissing numbers
The E8 lattice is remarkable in that it gives solutions to the lattice packing problem and the kissing number problemKissing number problem
In geometry, a kissing number is defined as the number of non-overlapping unit spheres that touch another given unit sphere. For a lattice packing the kissing number is the same for every sphere, but for an arbitrary sphere packing the kissing number may vary from one sphere to another...
in 8 dimensions.
The general sphere packing problem asks what is the densest way to pack n-dimensional (solid) spheres in Rn so that no two spheres overlap. Lattice packings are special types of sphere packings where the spheres are centered at the points of a lattice. Placing spheres of radius 1/√2 at the points of the E8 lattice gives a lattice packing in R8 with a density of
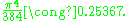
It is known that this is the maximum density that can be achieved by a lattice packing in 8 dimensions. Furthermore, the E8 lattice is the unique lattice (up to isometries and rescalings) with this density. It is conjectured this density is, in fact, optimal (even among irregular packings). Researchers have recently shown that no irregular packing density can exceed that of the E8 lattice by a factor of more than 1 + 10−14.
The kissing number problem asks what is the maximum number of spheres of a fixed radius that can touch (or "kiss") a central sphere of the same radius. In the E8 lattice packing mentioned above any given sphere touches 240 neighboring spheres. This is because there are 240 lattice vectors of minimum nonzero norm (the roots of the E8 lattice). It was shown in 1979 that this is the maximum possible number in 8-dimensions.
The kissing number problem is remarkably difficult and solutions are only known in 1, 2, 3, 4, 8, and 24 dimensions. Perhaps surprisingly, it is easier to find the solution in 8 (and 24) dimensions than in 3 or 4. This follows from the special properties of the E8 lattice (and its 24-dimensional cousin, the Leech lattice
Leech lattice
In mathematics, the Leech lattice is an even unimodular lattice Λ24 in 24-dimensional Euclidean space E24 found by .-History:Many of the cross-sections of the Leech lattice, including the Coxeter–Todd lattice and Barnes–Wall lattice, in 12 and 16 dimensions, were found much earlier than...
).
Theta function
One can associate to any (positive-definite) lattice Λ a theta function given byThe theta function of a lattice is then a holomorphic function
Holomorphic function
In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
on the upper half-plane. Furthermore, the theta function of an even unimodular lattice of rank n is actually a modular form
Modular form
In mathematics, a modular form is a analytic function on the upper half-plane satisfying a certain kind of functional equation and growth condition. The theory of modular forms therefore belongs to complex analysis but the main importance of the theory has traditionally been in its connections...
of weight n/2. The theta function of an integral lattice is often written as a power series in
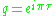so that the coefficient of qn gives the number of lattice vectors of norm n.Up to normalization, there is a unique modular form of weight 4: the Eisenstein series
Eisenstein series
Eisenstein series, named after German mathematician Gotthold Eisenstein, are particular modular forms with infinite series expansions that may be written down directly...
G4(τ). The theta function for the E8 lattice must then be proportional to G4(τ). The normalization can be fixed by noting that there is a unique vector of norm 0. This gives
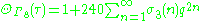
where σ3(n) is the divisor function
Divisor function
In mathematics, and specifically in number theory, a divisor function is an arithmetical function related to the divisors of an integer. When referred to as the divisor function, it counts the number of divisors of an integer. It appears in a number of remarkable identities, including relationships...
. It follows that the number of E8 lattice vectors of norm 2n is 240 times the sum of the cubes of the divisors of n. The first few terms of this series are given by :
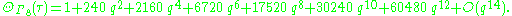
The E8 theta function may be written in terms of the Jacobi theta functions as follows:
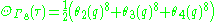
where
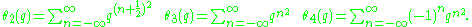
Hamming code
The E8 lattice is very closely related to the Hamming codeHamming code
In telecommunication, Hamming codes are a family of linear error-correcting codes that generalize the Hamming-code invented by Richard Hamming in 1950. Hamming codes can detect up to two and correct up to one bit errors. By contrast, the simple parity code cannot correct errors, and can detect only...
H(8,4) and can, in fact, be constructed from it. The Hamming code H(8,4) is a binary code
Linear code
In coding theory, a linear code is an error-correcting code for which any linear combination of codewords is also a codeword. Linear codes are traditionally partitioned into block codes and convolutional codes, although Turbo codes can be seen as a hybrid of these two types. Linear codes allow for...
of length 8 and rank 4; that is, it is a 4-dimensional subspace of the finite vector space (F2)8. Writing elements of (F2)8 as 8-bit integers in hexadecimal
Hexadecimal
In mathematics and computer science, hexadecimal is a positional numeral system with a radix, or base, of 16. It uses sixteen distinct symbols, most often the symbols 0–9 to represent values zero to nine, and A, B, C, D, E, F to represent values ten to fifteen...
, the code H(8,4) can by given explicitly as the set
- {00, 0F, 33, 3C, 55, 5A, 66, 69, 96, 99, A5, AA, C3, CC, F0, FF}
The code H(8,4) is significant partly because it is a Type II self-dual code. It has a minimum Hamming weight
Hamming weight
The Hamming weight of a string is the number of symbols that are different from the zero-symbol of the alphabet used. It is thus equivalent to the Hamming distance from the all-zero string of the same length. For the most typical case, a string of bits, this is the number of 1's in the string...
4, meaning that any two codewords differ by at least 4 bits. It is the largest length 8 binary code with this property.
One can construct a lattice Λ from a binary code C of length n by taking the set of all vectors x in Zn such that x is congruent (modulo 2) to a codeword of C. It is often convenient to rescale Λ by a factor of 1/√2,
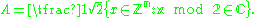
Applying this construction a Type II self-dual code gives an even, unimodular lattice. In particular, applying it to the Hamming code H(8,4) gives an E8 lattice. It is not entirely trivial, however, to find an explicit isomorphism between this lattice and the lattice Γ8 defined above.
Integral octonions
The E8 lattice is also closely related to the nonassociative algebra of real octonionOctonion
In mathematics, the octonions are a normed division algebra over the real numbers, usually represented by the capital letter O, using boldface O or blackboard bold \mathbb O. There are only four such algebras, the other three being the real numbers R, the complex numbers C, and the quaternions H...
s O. It is possible to define the concept of an integral octonion analogous to that of an integral quaternion. The integral octonions naturally form a lattice inside O. This lattice is just a rescaled E8 lattice. (The minimum norm in the integral octonion lattice is 1 rather than 2). Embedded in the octonions in this manner the E8 lattice takes on the structure of a nonassociative ring
Nonassociative ring
In abstract algebra, a nonassociative ring is a generalization of the concept of ring.A nonassociative ring is a set R with two operations, addition and multiplication, such that:# R is an abelian group under addition:## a+b = b+a...
.
Fixing a basis (1, i, j, k, ℓ, ℓi, ℓj, ℓk) of unit octonions,
one can define the integral octonions as a maximal order containing this basis. (One must, of course, extend the definitions of order and ring to include the nonassociative case). This amounts to finding the largest subring
Subring
In mathematics, a subring of R is a subset of a ring, is itself a ring with the restrictions of the binary operations of addition and multiplication of R, and which contains the multiplicative identity of R...
of O containing the units on which the expressions x*x (the norm of x) and x + x* (twice the real part of x) are integer-valued. There are actually seven such maximal orders, one corresponding to each of the seven imaginary units. However, all seven maximal orders are isomorphic. One such maximal order is generated by the octonions i, j, and ½ (i + j + k + ℓ).
A detailed account of the integral octonions and their relation to the E8 lattice can be found in Conway and Smith (2003).
Example definition of integral octonions
Consider octonion multiplication defined by triads: 123, 145, 167, 246, 275, 374, 365. Then integral octonions form vectors:1)
, i=0,1,...,72)
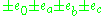, indexes abc span triads: 123, 145, 167, 346, 375, 274, 2653)
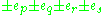, indexes pqrs span fours: 1246, 1257, 1347, 1356, 2345, 2367, 4567Imaginary octonions in this set (14 from point 1 and 7*16=112 from point 3) form roots of Lie algebra
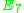. Adding remaining 2+112 vectors we obtain 240 vectors which form roots of Lie algebra 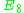. See the Koca work on this subject.Applications
In 1982 Michael FreedmanMichael Freedman
Michael Hartley Freedman is a mathematician at Microsoft Station Q, a research group at the University of California, Santa Barbara. In 1986, he was awarded a Fields Medal for his work on the Poincaré conjecture. Freedman and Robion Kirby showed that an exotic R4 manifold exists.Freedman was born...
produced a bizarre example of a topological 4-manifold
4-manifold
In mathematics, 4-manifold is a 4-dimensional topological manifold. A smooth 4-manifold is a 4-manifold with a smooth structure. In dimension four, in marked contrast with lower dimensions, topological and smooth manifolds are quite different...
, called the E8 manifold
E8 manifold
In mathematics, the E8 manifold is the unique compact, simply connected topological 4-manifold with intersection form the E8 lattice.The E8 manifold was discovered by Michael Freedman in 1982...
, whose intersection form
Intersection form
Intersection form may refer to:*Intersection theory *intersection form...
is given by the E8 lattice. This manifold is an example of a topological manifold which admits no smooth structure
Smooth structure
In mathematics, a smooth structure on a manifold allows for an unambiguous notion of smooth function. In particular, a smooth structure allows one to perform mathematical analysis on the manifold....
and is not even triangulable
Triangulation (topology)
In mathematics, topology generalizes the notion of triangulation in a natural way as follows:A triangulation of a topological space X is a simplicial complex K, homeomorphic to X, together with a homeomorphism h:K\to X....
.
In string theory
String theory
String theory is an active research framework in particle physics that attempts to reconcile quantum mechanics and general relativity. It is a contender for a theory of everything , a manner of describing the known fundamental forces and matter in a mathematically complete system...
, the heterotic string
Heterotic string
In physics, a heterotic string is a peculiar mixture of the bosonic string and the superstring...
is a peculiar hybrid of a 26-dimensional bosonic string and a 10-dimensional superstring. In order for the theory to work correctly, the 16 mismatched dimensions must be compactified on an even, unimodular lattice of rank 16. There are two such lattices: Γ8⊕Γ8 and Γ16 (constructed in a fashion analogous to that of Γ8). These lead to two version of the heterotic string known as the E8×E8 heterotic string and the SO(32) heterotic string.
See also
- Leech latticeLeech latticeIn mathematics, the Leech lattice is an even unimodular lattice Λ24 in 24-dimensional Euclidean space E24 found by .-History:Many of the cross-sections of the Leech lattice, including the Coxeter–Todd lattice and Barnes–Wall lattice, in 12 and 16 dimensions, were found much earlier than...
- E8 (mathematics)E8 (mathematics)In mathematics, E8 is any of several closely related exceptional simple Lie groups, linear algebraic groups or Lie algebras of dimension 248; the same notation is used for the corresponding root lattice, which has rank 8...
- Semiregular E-polytopeSemiregular E-polytopeIn geometry, a uniform k21 polytope is a polytope in k + 4 dimensions constructed from the En Coxeter group, and having only regular polytope facets...