Hadamard matrix
Encyclopedia
In mathematics
, an Hadamard matrix, named after the French mathematician
Jacques Hadamard
, is a square matrix whose entries are either +1 or −1 and whose rows are mutually orthogonal. In geometric terms, this means that every two different rows in a Hadamard matrix represent two perpendicular
vector
s, while in combinatorial
terms, it means that every two different rows have matching entries in exactly half of their columns and mismatched entries in the remaining columns. It is a consequence of this definition that the corresponding properties hold for columns as well as rows. The n-dimensional parallelotope
spanned by the rows of an n×n Hadamard matrix has the maximum possible n-dimensional volume
among parallelotopes spanned by vectors whose entries are bounded in absolute value
by 1. Equivalently, a Hadamard matrix has maximal determinant among matrices with entries of absolute value less than or equal to 1.
Certain Hadamard matrices can almost directly be used as an error-correcting code using a Hadamard code
(generalized in Reed–Muller code
s), and are also used in balanced repeated replication
(BRR), used by statistician
s to estimate the variance
of a parameter
estimator
.
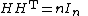
where In is the n × n identity matrix
and HT is the transpose
of H. Consequently the determinant
of H equals ±nn/2.
Suppose that M is a complex matrix of order n, whose entries are bounded by |Mij| ≤1, for each i, j between 1 and n. Then Hadamard's determinant bound
states that
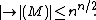
Equality in this bound is attained for a real matrix M if and only if M is a Hadamard matrix.
The order of a Hadamard matrix must be 1, 2, or a multiple of 4.
in 1867. Let H be a Hadamard matrix of order n. Then the partitioned matrix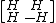
is a Hadamard matrix of order 2n. This observation can be applied repeatedly and leads to the following sequence of matrices, also called Walsh matrices
.
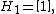
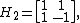
and
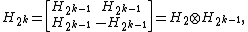
for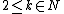
, where 
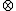denotes the Kronecker product
.
In this manner, Sylvester constructed Hadamard matrices of order 2k for every non-negative integer k.
Sylvester's matrices have a number of special properties. They are symmetric and traceless. The elements in the first column and the first row are all positive. The elements in all the other rows and columns are evenly divided between positive and negative
. Sylvester matrices are closely connected with Walsh function
s.
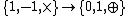, we can describe an alternative construction of Sylvester's Hadamard matrix. First consider the matrix 
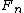, the 
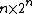matrix whose columns consist of all n-bit numbers arranged in ascending counting order. We may define 
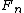recursively by
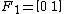
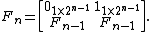
It can be shown by induction that the image of the Hadamard matrix under the above homomorphism is given by
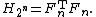
This construction demonstrates that the rows of the Hadamard matrix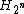
can be viewed as a length 
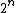linear error-correcting code of rank n, and minimum distance 
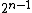with generating matrix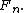 
This code is also referred to as a Walsh code
. The Hadamard code
, by contrast, is constructed from the Hadamard matrix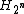
by a slightly different procedure.
Sylvester's 1867 construction yields Hadamard matrices of order 1, 2, 4, 8, 16, 32, etc. Hadamard matrices of orders 12 and 20 were subsequently constructed by Hadamard (in 1893). In 1933 Raymond Paley
discovered a construction that produces a Hadamard matrix of order q+1 when q is any prime
power that is congruent
to 3 modulo 4 and that produces a Hadamard matrix of order 2(q+1) when q is a prime power that is congruent to 1 modulo 4. His method uses finite field
s. The Hadamard conjecture should probably be attributed to Paley.
The smallest order that cannot be constructed by a combination of Sylvester's and Paley's methods is 92. A Hadamard matrix of this order was found using a computer by Baumert, Golomb
, and Hall
in 1962. They used a construction, due to Williamson, that has yielded many additional orders. Many other methods for constructing Hadamard matrices are now known.
In 2005, Hadi Kharaghani and Behruz Tayfeh-Rezaie published their construction of a Hadamard matrix of order 428. As a result, the smallest order for which no Hadamard matrix is presently known is 668.
, there are 13 multiples of 4 less than or equal to 2000 for which no Hadamard matrix of that order is known. They are:
668, 716, 892, 1004, 1132, 1244, 1388, 1436, 1676, 1772, 1916, 1948, 1964.
if one can be obtained from the other by negating rows or columns, or by interchanging rows or columns. Up to equivalence, there is a unique Hadamard matrix of orders 1, 2, 4, 8, and 12. There are 5 inequivalent matrices of order 16, 3 of order 20, 60 of order 24, and 487 of order 28. Millions of inequivalent matrices are known for orders 32, 36, and 40. Using a coarser notion of equivalence that also allows transposition, there are 4 inequivalent matrices of order 16, 3 of order 20, 36 of order 24, and 294 of order 28 .
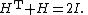
Reid and Brown in 1972 showed that there exists a "doubly regular tournament
of order n" if and only if there exists a skew Hadamard matrix of order n+1.
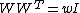for some w, its weight. A weighing matrix with its weight equal to its order is a Hadamard matrix.
Another generalization defines a complex Hadamard matrix to be a matrix in which the entries are complex numbers of unit modulus
and which satisfies H H*= n In where H* is the conjugate transpose
of H. Complex Hadamard matrices arise in the study of operator algebras and the theory of quantum computation.
Butson-type Hadamard matrices
are complex Hadamard matrices in which the entries are taken to be qth roots of unity. The term "complex Hadamard matrix" has been used by some authors to refer specifically to the case q = 4.
Regular Hadamard matrices are real Hadamard matrices whose row and column sums are all equal. A necessary condition on the existence of a regular n×n Hadamard matrix is that n be a perfect square. A circulant matrix is manifestly regular, and therefore a circulant Hadamard matrix would have to be of perfect square order. Moreover, if an n×n circulant Hadamard
matrix existed with n>1 then n would necessarily have to be of the form 4u2 with u odd.
The circulant Hadamard matrix conjecture, however, asserts that, apart from the known 1×1 and 4×4 examples, no such matrices exist. This was verified for all but 26 values of u less than 104. In 2011, an attempted proof of the circulant Hadamard matrix conjecture was published. However, this attempted proof depends on the commutativity of two matrix operators which do not, in general, commute.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, an Hadamard matrix, named after the French mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
Jacques Hadamard
Jacques Hadamard
Jacques Salomon Hadamard FRS was a French mathematician who made major contributions in number theory, complex function theory, differential geometry and partial differential equations.-Biography:...
, is a square matrix whose entries are either +1 or −1 and whose rows are mutually orthogonal. In geometric terms, this means that every two different rows in a Hadamard matrix represent two perpendicular
Perpendicular
In geometry, two lines or planes are considered perpendicular to each other if they form congruent adjacent angles . The term may be used as a noun or adjective...
vector
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
s, while in combinatorial
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
terms, it means that every two different rows have matching entries in exactly half of their columns and mismatched entries in the remaining columns. It is a consequence of this definition that the corresponding properties hold for columns as well as rows. The n-dimensional parallelotope
Parallelepiped
In geometry, a parallelepiped is a three-dimensional figure formed by six parallelograms. By analogy, it relates to a parallelogram just as a cube relates to a square. In Euclidean geometry, its definition encompasses all four concepts...
spanned by the rows of an n×n Hadamard matrix has the maximum possible n-dimensional volume
Volume
Volume is the quantity of three-dimensional space enclosed by some closed boundary, for example, the space that a substance or shape occupies or contains....
among parallelotopes spanned by vectors whose entries are bounded in absolute value
Absolute value
In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
by 1. Equivalently, a Hadamard matrix has maximal determinant among matrices with entries of absolute value less than or equal to 1.
Certain Hadamard matrices can almost directly be used as an error-correcting code using a Hadamard code
Hadamard code
The Hadamard code is an error-correcting code that is used for error detection and correction when transmitting messages over very noisy or unreliable channels....
(generalized in Reed–Muller code
Reed–Muller code
Reed–Muller codes are a family of linear error-correcting codes used in communications. Reed–Muller codes belong to the classes of locally testable codes and locally decodable codes, which is why they are useful in the design of probabilistically checkable proofs in computational complexity theory....
s), and are also used in balanced repeated replication
Balanced repeated replication
Balanced repeated replication is a statistical technique for estimating the sampling variability of a statistic obtained by stratified sampling.- Outline of the technique :# Select balanced half-samples from the full sample....
(BRR), used by statistician
Statistician
A statistician is someone who works with theoretical or applied statistics. The profession exists in both the private and public sectors. The core of that work is to measure, interpret, and describe the world and human activity patterns within it...
s to estimate the variance
Variance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
of a parameter
Parameter
Parameter from Ancient Greek παρά also “para” meaning “beside, subsidiary” and μέτρον also “metron” meaning “measure”, can be interpreted in mathematics, logic, linguistics, environmental science and other disciplines....
estimator
Estimator
In statistics, an estimator is a rule for calculating an estimate of a given quantity based on observed data: thus the rule and its result are distinguished....
.
Properties
It follows from the definition that a Hadamard matrix H of order n satisfies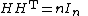where In is the n × n identity matrix
Identity matrix
In linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
and HT is the transpose
Transpose
In linear algebra, the transpose of a matrix A is another matrix AT created by any one of the following equivalent actions:...
of H. Consequently the determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
of H equals ±nn/2.
Suppose that M is a complex matrix of order n, whose entries are bounded by |Mij| ≤1, for each i, j between 1 and n. Then Hadamard's determinant bound
Hadamard's inequality
In mathematics, Hadamard's inequality, first published by Jacques Hadamard in 1893, is a bound on the determinant of a matrix whose entries are complex numbers in terms of the lengths of its column vectors...
states that
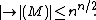
Equality in this bound is attained for a real matrix M if and only if M is a Hadamard matrix.
The order of a Hadamard matrix must be 1, 2, or a multiple of 4.
Sylvester's construction
Examples of Hadamard matrices were actually first constructed by James Joseph SylvesterJames Joseph Sylvester
James Joseph Sylvester was an English mathematician. He made fundamental contributions to matrix theory, invariant theory, number theory, partition theory and combinatorics...
in 1867. Let H be a Hadamard matrix of order n. Then the partitioned matrix
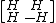
is a Hadamard matrix of order 2n. This observation can be applied repeatedly and leads to the following sequence of matrices, also called Walsh matrices
Walsh matrix
In mathematics, a Walsh matrix is a specific square matrix, with dimensions a power of 2, the entries of which are +1 or −1, and the property that the dot product of any two distinct rows is zero. The Walsh matrix was proposed by Joseph Leonard Walsh in 1923...
.
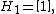
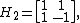
and
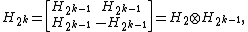
for
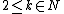, where 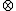denotes the Kronecker productKronecker product
In mathematics, the Kronecker product, denoted by ⊗, is an operation on two matrices of arbitrary size resulting in a block matrix. It gives the matrix of the tensor product with respect to a standard choice of basis. The Kronecker product should not be confused with the usual matrix...
.
In this manner, Sylvester constructed Hadamard matrices of order 2k for every non-negative integer k.
Sylvester's matrices have a number of special properties. They are symmetric and traceless. The elements in the first column and the first row are all positive. The elements in all the other rows and columns are evenly divided between positive and negative
Sign (mathematics)
In mathematics, the word sign refers to the property of being positive or negative. Every nonzero real number is either positive or negative, and therefore has a sign. Zero itself is signless, although in some contexts it makes sense to consider a signed zero...
. Sylvester matrices are closely connected with Walsh function
Walsh function
In mathematical analysis, the set of Walsh functions form an orthogonal basis of the square-integrable functions on the unit interval. The functions take the values -1 and +1 only, on sub-intervals defined by dyadic fractions...
s.
Alternative construction
If we map the elements of the Hadamard matrix using the group homomorphismGroup homomorphism
In mathematics, given two groups and , a group homomorphism from to is a function h : G → H such that for all u and v in G it holds that h = h \cdot h...
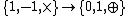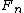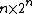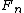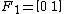
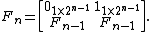
, we can describe an alternative construction of Sylvester's Hadamard matrix. First consider the matrix , the matrix whose columns consist of all n-bit numbers arranged in ascending counting order. We may define recursively byIt can be shown by induction that the image of the Hadamard matrix under the above homomorphism is given by
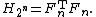
This construction demonstrates that the rows of the Hadamard matrix
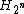can be viewed as a length 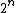linear error-correcting code of rank n, and minimum distance 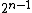with generating matrix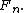 This code is also referred to as a Walsh code
Walsh code
In coding theory, the Walsh–Hadamard code, named after the American mathematician Joseph Leonard Walsh and the French mathematician Jacques Hadamard, is an example of a linear code over a binary alphabet that maps messages of length n to codewords of length 2^n...
. The Hadamard code
Hadamard code
The Hadamard code is an error-correcting code that is used for error detection and correction when transmitting messages over very noisy or unreliable channels....
, by contrast, is constructed from the Hadamard matrix
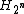by a slightly different procedure.The Hadamard conjecture
The most important open question in the theory of Hadamard matrices is that of existence. The Hadamard conjecture proposes that a Hadamard matrix of order 4k exists for every positive integer k.Sylvester's 1867 construction yields Hadamard matrices of order 1, 2, 4, 8, 16, 32, etc. Hadamard matrices of orders 12 and 20 were subsequently constructed by Hadamard (in 1893). In 1933 Raymond Paley
Raymond Paley
Raymond Edward Alan Christopher Paley was an English mathematician. Paley was born in Bournemouth, England. He was educated at Eton. From there he entered Trinity College, Cambridge where he showed himself the most brilliant student among a remarkable collection of fellow undergraduates...
discovered a construction that produces a Hadamard matrix of order q+1 when q is any prime
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
power that is congruent
Congruence relation
In abstract algebra, a congruence relation is an equivalence relation on an algebraic structure that is compatible with the structure...
to 3 modulo 4 and that produces a Hadamard matrix of order 2(q+1) when q is a prime power that is congruent to 1 modulo 4. His method uses finite field
Finite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
s. The Hadamard conjecture should probably be attributed to Paley.
The smallest order that cannot be constructed by a combination of Sylvester's and Paley's methods is 92. A Hadamard matrix of this order was found using a computer by Baumert, Golomb
Solomon W. Golomb
Solomon Wolf Golomb is an American mathematician and engineer and a professor of electrical engineering at the University of Southern California, best known to the general public and fans of mathematical games as the inventor of polyominoes, the inspiration for the computer game Tetris...
, and Hall
Marshall Hall (mathematician)
Marshall Hall, Jr. was an American mathematician who made contributions to group theory and combinatorics.- Career :...
in 1962. They used a construction, due to Williamson, that has yielded many additional orders. Many other methods for constructing Hadamard matrices are now known.
In 2005, Hadi Kharaghani and Behruz Tayfeh-Rezaie published their construction of a Hadamard matrix of order 428. As a result, the smallest order for which no Hadamard matrix is presently known is 668.
, there are 13 multiples of 4 less than or equal to 2000 for which no Hadamard matrix of that order is known. They are:
668, 716, 892, 1004, 1132, 1244, 1388, 1436, 1676, 1772, 1916, 1948, 1964.
Equivalence of Hadamard matrices
Two Hadamard matrices are considered equivalentEquivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
if one can be obtained from the other by negating rows or columns, or by interchanging rows or columns. Up to equivalence, there is a unique Hadamard matrix of orders 1, 2, 4, 8, and 12. There are 5 inequivalent matrices of order 16, 3 of order 20, 60 of order 24, and 487 of order 28. Millions of inequivalent matrices are known for orders 32, 36, and 40. Using a coarser notion of equivalence that also allows transposition, there are 4 inequivalent matrices of order 16, 3 of order 20, 36 of order 24, and 294 of order 28 .
Skew Hadamard matrices
A Hadamard matrix H is skew if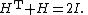Reid and Brown in 1972 showed that there exists a "doubly regular tournament
Tournament (graph theory)
A tournament is a directed graph obtained by assigning a direction for each edge in an undirected complete graph. That is, it is a directed graph in which every pair of vertices is connected by a single directed edge....
of order n" if and only if there exists a skew Hadamard matrix of order n+1.
Generalizations and special cases
Many generalizations and special cases of Hadamard matrices have been investigated in the mathematical literature. One basic generalization is the weighing matrix, a square matrix in which entries may also be zero and which satisfies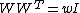 for some w, its weight. A weighing matrix with its weight equal to its order is a Hadamard matrix.Another generalization defines a complex Hadamard matrix to be a matrix in which the entries are complex numbers of unit modulus
Absolute value
In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
and which satisfies H H*= n In where H* is the conjugate transpose
Conjugate transpose
In mathematics, the conjugate transpose, Hermitian transpose, Hermitian conjugate, or adjoint matrix of an m-by-n matrix A with complex entries is the n-by-m matrix A* obtained from A by taking the transpose and then taking the complex conjugate of each entry...
of H. Complex Hadamard matrices arise in the study of operator algebras and the theory of quantum computation.
Butson-type Hadamard matrices
Butson-type Hadamard matrices
In mathematics, a complex Hadamard matrix H of size N with all its columns mutually orthogonal, belongs to the Butson-type H if all its elements are powers of q-th root of unity,- Existence :...
are complex Hadamard matrices in which the entries are taken to be qth roots of unity. The term "complex Hadamard matrix" has been used by some authors to refer specifically to the case q = 4.
Regular Hadamard matrices are real Hadamard matrices whose row and column sums are all equal. A necessary condition on the existence of a regular n×n Hadamard matrix is that n be a perfect square. A circulant matrix is manifestly regular, and therefore a circulant Hadamard matrix would have to be of perfect square order. Moreover, if an n×n circulant Hadamard
matrix existed with n>1 then n would necessarily have to be of the form 4u2 with u odd.
The circulant Hadamard matrix conjecture, however, asserts that, apart from the known 1×1 and 4×4 examples, no such matrices exist. This was verified for all but 26 values of u less than 104. In 2011, an attempted proof of the circulant Hadamard matrix conjecture was published. However, this attempted proof depends on the commutativity of two matrix operators which do not, in general, commute.
Practical applications
- Olivia MFSKOlivia MFSKOlivia MFSK is an amateur radioteletype protocol designed to work in difficult conditions on shortwave bands. The signal can still be properly copied when it is buried 10 dB below the noise floor...
– an amateur-radio digital protocol designed to work in difficult (low signal-to-noise ratio plus multipath propagation) conditions on shortwave bands. - Balanced Repeated ReplicationBalanced repeated replicationBalanced repeated replication is a statistical technique for estimating the sampling variability of a statistic obtained by stratified sampling.- Outline of the technique :# Select balanced half-samples from the full sample....
(BRR) – a technique used by statisticians to estimate the varianceVarianceIn probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
of a statistical estimator. - Coded apertureCoded apertureCoded Apertures or Coded-Aperture Masks are grids, gratings, or other patterns of materials opaque to various wavelengths of light. The wavelengths are usually high-energy radiation such as X-rays and gamma rays. By blocking and unblocking light in a known pattern, a coded "shadow" is cast upon a...
spectrometry – an instrument for measuring the spectrum of light. The mask element used in coded aperture spectrometers is often a variant of a Hadamard matrix.
External links
- Skew Hadamard matrices of all orders up to 100, including every type with order up to 28;
- N.J.A. Sloane's Library of Hadamard Matrices
- On-line utility to obtain all orders up to 1000, except 668, 716, 876 & 892.
- On Hotelling's Weighing Problem, Alexander M. Mood, Ann. Math. Statist. Volume 17, Number 4 (1946), 432–446.