Hadamard code
Encyclopedia
Error detection and correction
In information theory and coding theory with applications in computer science and telecommunication, error detection and correction or error control are techniques that enable reliable delivery of digital data over unreliable communication channels...
when transmitting messages over very noisy or unreliable channels.
A famous application of the Hadamard code was the NASA space probe Mariner 9
Mariner 9
Mariner 9 was a NASA space orbiter that helped in the exploration of Mars and was part of the Mariner program. Mariner 9 was launched toward Mars on May 30, 1971 from Cape Canaveral Air Force Station and reached the planet on November 13 of the same year, becoming the first spacecraft to orbit...
in 1971, where the code was used to transmit photos of Mars back to Earth.
Because of its unique mathematical properties, the Hadamard code is not only used by engineers, but also intensely studied in coding theory
Coding theory
Coding theory is the study of the properties of codes and their fitness for a specific application. Codes are used for data compression, cryptography, error-correction and more recently also for network coding...
, mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, and theoretical computer science
Theoretical computer science
Theoretical computer science is a division or subset of general computer science and mathematics which focuses on more abstract or mathematical aspects of computing....
.
The Hadamard code is named after Jacques Hadamard
Jacques Hadamard
Jacques Salomon Hadamard FRS was a French mathematician who made major contributions in number theory, complex function theory, differential geometry and partial differential equations.-Biography:...
and also known under the names Walsh code and Walsh–Hadamard code.
The Hadamard code maps a message consisting of
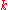bits to a codeword of 
bits; it is able to detect 
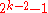errors and to correct 
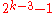errors. In standard coding theory notation for block codeBlock code
In coding theory, block codes refers to the large and important family of error-correcting codes that encode data in blocks.There is a vast number of examples for block codes, many of which have a wide range of practical applications...
s, the Hadamard code is a
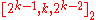-code, that is, it is a linear codeLinear code
In coding theory, a linear code is an error-correcting code for which any linear combination of codewords is also a codeword. Linear codes are traditionally partitioned into block codes and convolutional codes, although Turbo codes can be seen as a hybrid of these two types. Linear codes allow for...
over a binary alphabet
Binary alphabet
Binary alphabet may refer to:* The members of a binary set in mathematical set theory* ASCII...
, has block length
, message length (or dimension)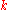 
, and minimum distance 
. For large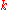 
, the block length is very large, but many errors can be corrected. The Hadamard code of message length k is the same as the first order Reed–Muller codeReed–Muller code
Reed–Muller codes are a family of linear error-correcting codes used in communications. Reed–Muller codes belong to the classes of locally testable codes and locally decodable codes, which is why they are useful in the design of probabilistically checkable proofs in computational complexity theory....
RM(1,k−1).
Normally, Hadamard codes are based on Sylvester's construction of Hadamard matrices, but the term “Hadamard code” is also used to refer to codes constructed from arbitrary Hadamard matrices
Hadamard matrix
In mathematics, an Hadamard matrix, named after the French mathematician Jacques Hadamard, is a square matrix whose entries are either +1 or −1 and whose rows are mutually orthogonal...
, which are not necessarily of Sylvester type.
In general, such a code is not linear.
Such codes were first constructed by R. C. Bose and S. S. Shrikhande in 1959. If n is the size of the Hadamard matrix, the code has parameters
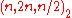, meaning it is a not-necessarily-linear binary code with 2n codewords of block length n and minimal distance n/2. The construction and decoding scheme described below apply for general n, but the property of linearity and the identification with Reed–Muller codes require that n be a power of 2 and that the Hadamard matrix be equivalent to the matrix constructed by Sylvester's method.History
Hadamard code is the name that is most commonly used for this code in the literature.Jacques Hadamard
Jacques Hadamard
Jacques Salomon Hadamard FRS was a French mathematician who made major contributions in number theory, complex function theory, differential geometry and partial differential equations.-Biography:...
did not invent the code himself, but he defined Hadamard matrices
Hadamard matrix
In mathematics, an Hadamard matrix, named after the French mathematician Jacques Hadamard, is a square matrix whose entries are either +1 or −1 and whose rows are mutually orthogonal...
around 1893, long before the first error-correcting code, the Hamming code
Hamming code
In telecommunication, Hamming codes are a family of linear error-correcting codes that generalize the Hamming-code invented by Richard Hamming in 1950. Hamming codes can detect up to two and correct up to one bit errors. By contrast, the simple parity code cannot correct errors, and can detect only...
, was developed in the 1940s.
The Hadamard code is based on Hadamard matrices, and while there are many different Hadamard matrices that could be used here, normally only Sylvester's construction of Hadamard matrices is used to obtain the codewords of the Hadamard code.
James Joseph Sylvester
James Joseph Sylvester
James Joseph Sylvester was an English mathematician. He made fundamental contributions to matrix theory, invariant theory, number theory, partition theory and combinatorics...
developed his construction of Hadamard matrices in 1867, which actually predates Hadamard's work on Hadamard matrices.
Hence the name Hadamard code is not undisputed and sometimes the code is called Walsh code, honoring the American mathematician Joseph Leonard Walsh
Joseph Leonard Walsh
Joseph Leonard Walsh, was an American mathematician. His work was mainly in the field of analysis.For most of his professional career he studied and worked at Harvard University. He received a B.S. in 1916 and a PhD in 1920. The Advisor of his PhD was Maxime Bôcher...
.
A Hadamard code was used during the 1971 Mariner 9
Mariner 9
Mariner 9 was a NASA space orbiter that helped in the exploration of Mars and was part of the Mariner program. Mariner 9 was launched toward Mars on May 30, 1971 from Cape Canaveral Air Force Station and reached the planet on November 13 of the same year, becoming the first spacecraft to orbit...
mission to correct for picture transmission errors. The data words used during this mission were 6 bits long, which represented 64 grayscale
Grayscale
In photography and computing, a grayscale or greyscale digital image is an image in which the value of each pixel is a single sample, that is, it carries only intensity information...
values.
Because of limitations of the quality of the alignment of the transmitter the maximum useful data length was about 30 bits. Instead of using a repetition code
Repetition code
In coding theory, the repetition code is one of the most basic error-correcting codes. In order to transmit a message over a noisy channel that may corrupt the transmission in a few places, the idea of the repetition code is to just repeat the message several times. The hope is that the channel...
, a [32, 6, 16] Hadamard code was used. Errors of up to 7 bits per word could be corrected using this scheme. Compared to a 5-repetition code
Repetition code
In coding theory, the repetition code is one of the most basic error-correcting codes. In order to transmit a message over a noisy channel that may corrupt the transmission in a few places, the idea of the repetition code is to just repeat the message several times. The hope is that the channel...
, the error correcting properties of this Hadamard code are much better, yet its rate is comparable.
The efficient decoding algorithm was an important factor in the decision to use this code. The circuitry used was called the "Green Machine". It employed the fast Fourier transform
Fast Fourier transform
A fast Fourier transform is an efficient algorithm to compute the discrete Fourier transform and its inverse. "The FFT has been called the most important numerical algorithm of our lifetime ." There are many distinct FFT algorithms involving a wide range of mathematics, from simple...
which can increase the decoding speed by a factor of 3.
Since the 1990s use of this code by space programs has more or less ceased, and the Deep Space Network does not support this error correction scheme for its dishes that are greater than 26m.
Construction
While all Hadamard codes are based on Hadamard matrices, the constructions differ in subtle ways for different scientific fields, authors, and uses.Engineers, who use the codes for data transmission, and coding theorists
Coding theory
Coding theory is the study of the properties of codes and their fitness for a specific application. Codes are used for data compression, cryptography, error-correction and more recently also for network coding...
, who analyze extremal properties of codes, typically want the rate of the code to be as high as possible, even if this means that the construction becomes mathematically slightly less elegant.
On the other hand, for many applications of Hadamard codes in theoretical computer science
Theoretical computer science
Theoretical computer science is a division or subset of general computer science and mathematics which focuses on more abstract or mathematical aspects of computing....
it is not so important to achieve the optimal rate, and hence simpler constructions of Hadamard codes are preferred since they can be analyzed more elegantly.
Construction with higher rate
The Hadamard code is obtained from an n-by-n Hadamard matrixHadamard matrix
In mathematics, an Hadamard matrix, named after the French mathematician Jacques Hadamard, is a square matrix whose entries are either +1 or −1 and whose rows are mutually orthogonal...
H.
In particular, the 2n codewords of the Hadamard code are the rows of H and the rows of −H.
To obtain a code over the alphabet {0,1}, the mapping −1 ↦ 1, 1 ↦ 0, or, equivalently, x ↦ log−1 x, is applied to the matrix elements. That the minimum distance of the code is n/2 follows from the defining property of Hadamard matrices, namely that their rows are mutually orthogonal.
This implies that two distinct rows of a Hadamard matrix differ in exactly n/2 positions, and, since negation of a row does not affect orthogonality, that any row of H differs from any row of −H in n/2 positions as well, except when the rows correspond, in which case they differ in n positions.
For the linear code, where n = 2k-1 and H is of Sylvester type, the message length is log2(2n) = k. A generator matrix
Generator matrix
In coding theory, a generator matrix is a basis for a linear code, generating all its possible codewords.If the matrix is G and the linear code is C,where w is a codeword of the linear code C, c is a row vector, and a bijection exists between w and c. A generator matrix for an q-code has...
for this code can be constructed by forming the (k−1)×2k−1 matrix
where
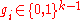is the vector corresponding to the binary representationBinary numeral system
The binary numeral system, or base-2 number system, represents numeric values using two symbols, 0 and 1. More specifically, the usual base-2 system is a positional notation with a radix of 2...
of
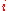,and then inserting and additional all-one vector as row 1. In other words,
is the list of all vectors of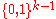 
in lexicographic order. For example, when k = 4, a generator matrix is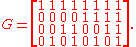
For general k, this generator matrix is a parity-check matrix
Parity-check matrix
In coding theory, a parity-check matrix of a linear block code Cis a generator matrix of the dual code. As such, a codeword c is in C if and only if the matrix-vector product Hc=0....
for the extended Hamming code of length 2k−1 and dimension 2k−1−k, which makes the Hadamard code the dual code of the extended Hamming code. Alternative constructions for the Hadamard code use its parity-check matrix or a recursive encoding process.
Elegant construction
In many theoretical applications of the Hadamard code, the rate does not matter so much. Here, a simpler construction than the above is used that roughly keeps the properties of the code the same.Most authors call this code also Hadamard code, but some texts refer to this simpler code as the Walsh–Hadamard code.
The codewords of the Walsh–Hadamard code consist of all rows of an n-by-n Hadamard matrix
Hadamard matrix
In mathematics, an Hadamard matrix, named after the French mathematician Jacques Hadamard, is a square matrix whose entries are either +1 or −1 and whose rows are mutually orthogonal...
H that is of Sylvester type, where again the mapping −1 ↦ 1, 1 ↦ 0 has been applied to the matrix elements.
This code has
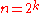codewords, but the block length is twice as large as above, that is, the rate is half of the rate of the above code. The Walsh–Hadamard code of dimension k−1 and the Hadamard code of dimension k both have block length k−1. The former is a subcode of the latter in which the complements of codewords are not codewords. In particular, in the Walsh–Hadamard code, the first letter of every codeword is 0 and therefore the all-one word is not a codeword.The
generator matrix for the Walsh–Hadamard code of dimensionDimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
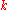is obtained from the generator matrix for the Hadamard matrix of dimension k+1, described above, by removing its first row.For example, the generator matrix for the Walsh–Hadamard code of dimension 3 is
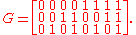
As is usual for linear codes generated by a generator matrix, we encode a message
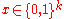, viewed as a row vector, by computing its codeword 
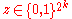using the vector-matrix product in the vector spaceVector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
over the finite field
:
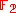This way, the matrix
defines a linear operator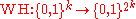 
and we can write 
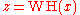.Equivalently,
can be defined using the scalar product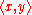 
over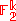 
:- For any two strings
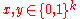, we have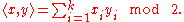 
Then
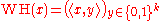, that is, the Walsh–Hadamard encoding of 
is the string consisting of all inner products with 
.Decoding
The code has minimum distance n/2 and hence can correct at most t = n/4 − 1 errors. The algorithm below achieves this.When a codeword is received it is first transformed to a ±1 vector v by changing all 0s to −1. Compute
(v HT). The entry with the maximum absolute value corresponds to the row taken as a codeword. If it is positive the codeword came from H; if it is negative the codeword came from −H.
Proof: If there were no errors the product (v HT) would be a vector consisting of zeros except for one entry of magnitude n. For each error in v, the dot product of v with a row of H changes by ±2. If there are no more than t errors, the zero entries become entries of magnitude no larger than 2t = n/2 − 2, and the entry of magnitude n becomes an entry of magnitude no smaller than n−2t = n/2+2. Consequently the entry with maximum absolute value remains maximal, and therefore points to the intended codeword. This argument also implies that the code can detect up to t+1 errors.