Block code
Encyclopedia
In coding theory
, block codes refers to the large and important family of error-correcting codes that encode data in blocks.
There is a vast number of examples for block codes, many of which have a wide range of practical applications. The main reason why the concept of block codes is so useful is that it allows coding theorists, mathematicians
, and computer scientists
to study the limitations of all block codes in a unified way.
Such limitations often take the form of bounds that relate different parameters of the block code to each other, such as its rate and its ability to detect and correct errors.
Examples of block codes are Reed–Solomon codes, Hamming code
s, Hadamard code
s, Expander code
s, Golay codes, and Reed–Muller code
s. These examples also belong to the class of linear code
s, and hence they are called linear block codes.
transmit digital data over unreliable communication channels subject to channel noise.
When a sender wants to transmit a possibly very long data stream using a block code, the sender breaks the stream up into pieces of some fixed size. Each such piece is called message and the procedure given by the block code encodes each message individually into a codeword, also called a block in the context of block codes. The sender then transmits all blocks to the receiver, who can in turn use some decoding mechanism to (hopefully) recover the original messages from the possibly corrupted received blocks.
The performance and success of the overall transmission depends on the parameters of the channel and the block code.
Formally, a block code is an injective mapping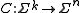 .
.
Here, is a finite and nonempty set and
is a finite and nonempty set and 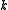 and
and  are integers. The meaning and significance of these three parameters and other parameters related to the code are described below.
are integers. The meaning and significance of these three parameters and other parameters related to the code are described below.
over some alphabet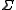 . The size
. The size  of the alphabet is often written as
of the alphabet is often written as 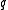 . If
. If  , then the block code is called a binary block code. In many applications it is useful to consider
, then the block code is called a binary block code. In many applications it is useful to consider  to be a prime power
to be a prime power
, and to identify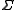 with the finite field
with the finite field
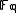 .
.
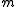 of
of 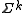 , that is, strings of length
, that is, strings of length 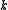 .
.
Hence the number is called the message length or dimension of a block code.
is called the message length or dimension of a block code.
 of a block code is the number of symbols in a block. Hence, the elements
of a block code is the number of symbols in a block. Hence, the elements  of
of 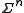 are strings of length
are strings of length  and correspond to blocks that may be received by the receiver. Hence they are also called received words.
and correspond to blocks that may be received by the receiver. Hence they are also called received words.
If for some message
for some message 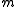 , then
, then  is called the codeword of
is called the codeword of 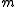 .
.
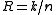 .
.
A large rate means that the amount of actual message per transmitted block is high. In this sense, the rate measures the transmission speed and the quantity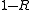 measures the overhead that occurs due to the encoding with the block code.
measures the overhead that occurs due to the encoding with the block code.
It is a simple information theoretical
fact that the rate cannot exceed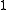 since data cannot be compressed in general. Formally, this follows from the fact that the code
since data cannot be compressed in general. Formally, this follows from the fact that the code 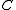 is an injective map.
is an injective map.
 of a block code is the minimum number of positions in which any two distinct codewords differ, and the relative distance
of a block code is the minimum number of positions in which any two distinct codewords differ, and the relative distance 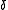 is the fraction
is the fraction 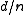 .
.
Formally, for received words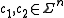 , let
, let  denote the Hamming distance
denote the Hamming distance
between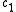 and
and 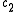 , that is, the number of positions in which
, that is, the number of positions in which 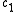 and
and  differ.
differ.
Then the minimum distance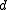 of the code
of the code  is defined as
is defined as .
.
Since any code has to be injective, any two codewords will disagree in at least one position, so the distance of any code is at least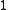 .
.
A larger distance allows for more error correction and detection.
For example, if we only consider errors that may change symbols of the sent codeword but never erase or add them, then the number of errors is the number of positions in which the sent codeword and the received word differ.
A code with distance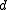 allows the receiver to detect up to
allows the receiver to detect up to 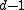 transmission errors since changing
transmission errors since changing 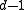 positions of a codeword can never accidentally yield another codeword. Furthermore, if no more than
positions of a codeword can never accidentally yield another codeword. Furthermore, if no more than  transmission errors occur, the receiver can uniquely decode the received word to a codeword. This is because every received word has at most one codeword at distance
transmission errors occur, the receiver can uniquely decode the received word to a codeword. This is because every received word has at most one codeword at distance 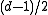 . If more than
. If more than 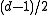 transmission errors occur, the receiver cannot uniquely decode the received word in general as there might be several possible codewords. One way for the receiver to cope with this situation is to use list-decoding, in which the decoder outputs a list of all codewords in a certain radius.
transmission errors occur, the receiver cannot uniquely decode the received word in general as there might be several possible codewords. One way for the receiver to cope with this situation is to use list-decoding, in which the decoder outputs a list of all codewords in a certain radius.
 is used as a shorthand for the fact that the block code under consideration is over an alphabet
is used as a shorthand for the fact that the block code under consideration is over an alphabet  of size
of size 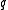 , has block length
, has block length  , message length
, message length 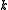 , and distance
, and distance 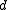 .
.
If the block code is a linear block code, then the square brackets in the notation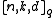 are used to represent that fact.
are used to represent that fact.
For binary codes with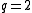 , the index is sometimes dropped.
, the index is sometimes dropped.
For maximum distance separable codes, the distance is always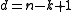 , and sometimes the precise distance is not known, non-trivial to prove or state, or not needed. In such cases, the
, and sometimes the precise distance is not known, non-trivial to prove or state, or not needed. In such cases, the  -component may be missing.
-component may be missing.
Sometimes, especially for non-block codes, the notation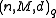 is used for codes that contain
is used for codes that contain 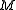 codewords of length
codewords of length  . For block codes with messages of length
. For block codes with messages of length 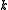 over an alphabet of size
over an alphabet of size 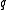 , this number would be
, this number would be 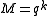 .
.
The first error-correcting code was the Hamming(7,4)-code
, developed by Richard W. Hamming in 1950. This code transform a message consisting of 4 bits into a codeword of 7 bits by adding 3 parity bits. Hence this code is a block code. It turns out that it is also a linear code and that it has distance 3. In the shorthand notation above, this means that the Hamming(7,4)-code is a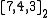 -code.
-code.
Reed-Solomon codes are a family of -codes with
-codes with 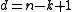 and
and 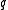 being a prime power
being a prime power
. Hadamard code
s are a family of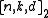 -codes with
-codes with 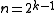 and
and 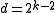 .
.
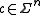 could be considered as a point in the
could be considered as a point in the  -dimension space
-dimension space 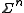 and the code
and the code 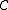 is the subset of
is the subset of  . A code
. A code 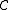 has distance
has distance 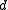 means that
means that 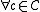 , there is no other codeword in the Hamming ball centered at
, there is no other codeword in the Hamming ball centered at  with radius
with radius 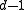 , which is defined as the collection of
, which is defined as the collection of  -dimension words whose Hamming distance
-dimension words whose Hamming distance
to is no more than
is no more than 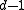 . Similarly,
. Similarly, 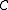 with (minimum) distance
with (minimum) distance 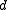 has the following properties:
has the following properties:
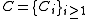 is called family of codes, where
is called family of codes, where 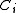 is an
is an 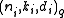 code with monotonic increasing
code with monotonic increasing 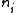 .
.
Rate of family of codes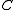 is defined as
is defined as 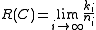
Relative distance of family of codes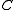 is defined as
is defined as 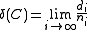
To explore the relationship between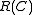 and
and 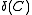 , a set of lower and upper bounds of block codes are known.
, a set of lower and upper bounds of block codes are known.
Hamming bound
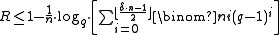
Singleton bound
The Singleton bound is that the sum of the rate and the relative distance of a block code cannot be much larger than 1: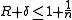 .
.
In other words, every block code satisfies the inequality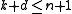 .
.
Reed–Solomon codes are non-trivial examples of codes that satisfy the singleton bound with equality.
Plotkin bound
For 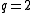 ,
, 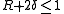
For the general case, the following Plotkin bounds holds for any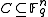 with distance
with distance 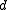 :
:
1. If
2. If >
> 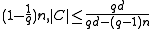
For any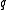 -ary code with distance
-ary code with distance  ,
, 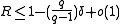
Gilbert–Varshamov bound
 , where
, where 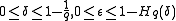 ,
,
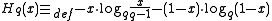 is the
is the 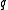 -ary entropy function.
-ary entropy function.
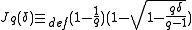 .
.
Let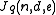 be the maximum number of codewords in a Hamming ball of radius
be the maximum number of codewords in a Hamming ball of radius  for any code
for any code  of distance
of distance 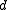 .
.
Then we have the Johnson Bound :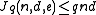 , if
, if 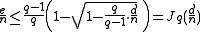
used in deep space communications uses 24 dimensions. If used as a binary code (which it usually is), the dimensions refer to the length of the codeword as defined above.
The theory of coding uses the N-dimensional sphere model. For example, how many pennies can be packed into a circle on a tabletop or in 3 dimensions, how many marbles can be packed into a globe. Other considerations enter the choice of a code. For example, hexagon packing into the constraint of a rectangular box will leave empty space at the corners. As the dimensions get larger, the percentage of empty space grows smaller. But at certain dimensions, the packing uses all the space and these codes are the so called perfect codes. There are very few of these codes.
Another property is the number of neighbors a single codeword may have.
Again, consider pennies as an example. First we pack the pennies in a rectangular grid. Each penny will have 4 near neighbors (and 4 at the corners which are farther away). In a hexagon, each penny will have 6 near neighbors. Respectively, in three and four dimensions, the maximum packing is given by the 12-face and 24-cell with 12 and 24 neighbors, respectively. When we increase the dimensions, the number of near neighbors increases very rapidly. In general, the value is given by the kissing numbers.
The result is the number of ways for noise to make the receiver choose
a neighbor (hence an error) grows as well. This is a fundamental limitation
of block codes, and indeed all codes. It may be harder to cause an error to
a single neighbor, but the number of neighbors can be large enough so the
total error probability actually suffers.
Coding theory
Coding theory is the study of the properties of codes and their fitness for a specific application. Codes are used for data compression, cryptography, error-correction and more recently also for network coding...
, block codes refers to the large and important family of error-correcting codes that encode data in blocks.
There is a vast number of examples for block codes, many of which have a wide range of practical applications. The main reason why the concept of block codes is so useful is that it allows coding theorists, mathematicians
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, and computer scientists
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
to study the limitations of all block codes in a unified way.
Such limitations often take the form of bounds that relate different parameters of the block code to each other, such as its rate and its ability to detect and correct errors.
Examples of block codes are Reed–Solomon codes, Hamming code
Hamming code
In telecommunication, Hamming codes are a family of linear error-correcting codes that generalize the Hamming-code invented by Richard Hamming in 1950. Hamming codes can detect up to two and correct up to one bit errors. By contrast, the simple parity code cannot correct errors, and can detect only...
s, Hadamard code
Hadamard code
The Hadamard code is an error-correcting code that is used for error detection and correction when transmitting messages over very noisy or unreliable channels....
s, Expander code
Expander code
In coding theory, expander codes are a type of linear block code that arises by using bipartite expander graphs. Along with concatenated codes, expander codes are interesting since they can construct binary codes with constant positive rate and relative distance...
s, Golay codes, and Reed–Muller code
Reed–Muller code
Reed–Muller codes are a family of linear error-correcting codes used in communications. Reed–Muller codes belong to the classes of locally testable codes and locally decodable codes, which is why they are useful in the design of probabilistically checkable proofs in computational complexity theory....
s. These examples also belong to the class of linear code
Linear code
In coding theory, a linear code is an error-correcting code for which any linear combination of codewords is also a codeword. Linear codes are traditionally partitioned into block codes and convolutional codes, although Turbo codes can be seen as a hybrid of these two types. Linear codes allow for...
s, and hence they are called linear block codes.
The block code and its parameters
Error-correcting codes are used to reliablyReliability (computer networking)
In computer networking, a reliable protocol is one that provides reliability properties with respect to the delivery of data to the intended recipient, as opposed to an unreliable protocol, which does not provide notifications to the sender as to the delivery of transmitted data.A reliable...
transmit digital data over unreliable communication channels subject to channel noise.
When a sender wants to transmit a possibly very long data stream using a block code, the sender breaks the stream up into pieces of some fixed size. Each such piece is called message and the procedure given by the block code encodes each message individually into a codeword, also called a block in the context of block codes. The sender then transmits all blocks to the receiver, who can in turn use some decoding mechanism to (hopefully) recover the original messages from the possibly corrupted received blocks.
The performance and success of the overall transmission depends on the parameters of the channel and the block code.
Formally, a block code is an injective mapping
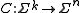 .
.Here,
 is a finite and nonempty set and
is a finite and nonempty set and 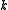 and
and  are integers. The meaning and significance of these three parameters and other parameters related to the code are described below.
are integers. The meaning and significance of these three parameters and other parameters related to the code are described below.The alphabet Σ
The data stream that has to be encoded is modeled as a stringString (computer science)
In formal languages, which are used in mathematical logic and theoretical computer science, a string is a finite sequence of symbols that are chosen from a set or alphabet....
over some alphabet
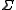 . The size
. The size  of the alphabet is often written as
of the alphabet is often written as 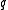 . If
. If  , then the block code is called a binary block code. In many applications it is useful to consider
, then the block code is called a binary block code. In many applications it is useful to consider  to be a prime power
to be a prime powerPrime power
In mathematics, a prime power is a positive integer power of a prime number.For example: 5=51, 9=32 and 16=24 are prime powers, while6=2×3, 15=3×5 and 36=62=22×32 are not...
, and to identify
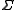 with the finite field
with the finite fieldFinite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
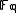 .
.The message length k
Messages are elements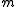 of
of 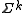 , that is, strings of length
, that is, strings of length 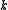 .
.Hence the number
 is called the message length or dimension of a block code.
is called the message length or dimension of a block code.The block length n
The block length of a block code is the number of symbols in a block. Hence, the elements
of a block code is the number of symbols in a block. Hence, the elements  of
of 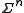 are strings of length
are strings of length  and correspond to blocks that may be received by the receiver. Hence they are also called received words.
and correspond to blocks that may be received by the receiver. Hence they are also called received words.If
 for some message
for some message 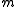 , then
, then  is called the codeword of
is called the codeword of 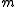 .
.The rate R
The rate of a block code is defined as the ratio between its message length and its block length: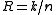 .
.A large rate means that the amount of actual message per transmitted block is high. In this sense, the rate measures the transmission speed and the quantity
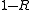 measures the overhead that occurs due to the encoding with the block code.
measures the overhead that occurs due to the encoding with the block code.It is a simple information theoretical
Information theory
Information theory is a branch of applied mathematics and electrical engineering involving the quantification of information. Information theory was developed by Claude E. Shannon to find fundamental limits on signal processing operations such as compressing data and on reliably storing and...
fact that the rate cannot exceed
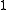 since data cannot be compressed in general. Formally, this follows from the fact that the code
since data cannot be compressed in general. Formally, this follows from the fact that the code 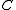 is an injective map.
is an injective map.The distance d
The distance or minimum distance of a block code is the minimum number of positions in which any two distinct codewords differ, and the relative distance
of a block code is the minimum number of positions in which any two distinct codewords differ, and the relative distance 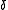 is the fraction
is the fraction 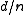 .
.Formally, for received words
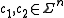 , let
, let  denote the Hamming distance
denote the Hamming distanceHamming distance
In information theory, the Hamming distance between two strings of equal length is the number of positions at which the corresponding symbols are different...
between
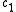 and
and 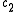 , that is, the number of positions in which
, that is, the number of positions in which 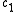 and
and  differ.
differ.Then the minimum distance
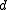 of the code
of the code  is defined as
is defined as .
.Since any code has to be injective, any two codewords will disagree in at least one position, so the distance of any code is at least
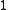 .
.A larger distance allows for more error correction and detection.
For example, if we only consider errors that may change symbols of the sent codeword but never erase or add them, then the number of errors is the number of positions in which the sent codeword and the received word differ.
A code with distance
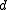 allows the receiver to detect up to
allows the receiver to detect up to 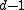 transmission errors since changing
transmission errors since changing 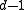 positions of a codeword can never accidentally yield another codeword. Furthermore, if no more than
positions of a codeword can never accidentally yield another codeword. Furthermore, if no more than  transmission errors occur, the receiver can uniquely decode the received word to a codeword. This is because every received word has at most one codeword at distance
transmission errors occur, the receiver can uniquely decode the received word to a codeword. This is because every received word has at most one codeword at distance 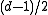 . If more than
. If more than 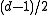 transmission errors occur, the receiver cannot uniquely decode the received word in general as there might be several possible codewords. One way for the receiver to cope with this situation is to use list-decoding, in which the decoder outputs a list of all codewords in a certain radius.
transmission errors occur, the receiver cannot uniquely decode the received word in general as there might be several possible codewords. One way for the receiver to cope with this situation is to use list-decoding, in which the decoder outputs a list of all codewords in a certain radius.Popular notation
The notation is used as a shorthand for the fact that the block code under consideration is over an alphabet
is used as a shorthand for the fact that the block code under consideration is over an alphabet  of size
of size 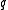 , has block length
, has block length  , message length
, message length 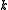 , and distance
, and distance 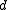 .
.If the block code is a linear block code, then the square brackets in the notation
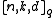 are used to represent that fact.
are used to represent that fact.For binary codes with
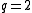 , the index is sometimes dropped.
, the index is sometimes dropped.For maximum distance separable codes, the distance is always
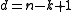 , and sometimes the precise distance is not known, non-trivial to prove or state, or not needed. In such cases, the
, and sometimes the precise distance is not known, non-trivial to prove or state, or not needed. In such cases, the  -component may be missing.
-component may be missing.Sometimes, especially for non-block codes, the notation
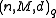 is used for codes that contain
is used for codes that contain 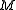 codewords of length
codewords of length  . For block codes with messages of length
. For block codes with messages of length 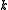 over an alphabet of size
over an alphabet of size 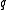 , this number would be
, this number would be 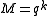 .
.Examples
As mentioned above, there is a vast number of error-correcting codes that are actually block codes.The first error-correcting code was the Hamming(7,4)-code
Hamming(7,4)
In coding theory, Hamming is a linear error-correcting code that encodes 4 bits of data into 7 bits by adding 3 parity bits. It is a member of a larger family of Hamming codes, but the term Hamming code often refers to this specific code that Richard W. Hamming introduced in 1950...
, developed by Richard W. Hamming in 1950. This code transform a message consisting of 4 bits into a codeword of 7 bits by adding 3 parity bits. Hence this code is a block code. It turns out that it is also a linear code and that it has distance 3. In the shorthand notation above, this means that the Hamming(7,4)-code is a
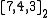 -code.
-code.Reed-Solomon codes are a family of
 -codes with
-codes with 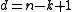 and
and 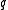 being a prime power
being a prime powerPrime power
In mathematics, a prime power is a positive integer power of a prime number.For example: 5=51, 9=32 and 16=24 are prime powers, while6=2×3, 15=3×5 and 36=62=22×32 are not...
. Hadamard code
Hadamard code
The Hadamard code is an error-correcting code that is used for error detection and correction when transmitting messages over very noisy or unreliable channels....
s are a family of
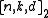 -codes with
-codes with 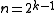 and
and 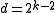 .
.Error detection and correction properties
A codeword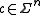 could be considered as a point in the
could be considered as a point in the  -dimension space
-dimension space 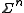 and the code
and the code 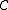 is the subset of
is the subset of  . A code
. A code 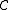 has distance
has distance 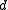 means that
means that 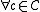 , there is no other codeword in the Hamming ball centered at
, there is no other codeword in the Hamming ball centered at  with radius
with radius 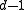 , which is defined as the collection of
, which is defined as the collection of  -dimension words whose Hamming distance
-dimension words whose Hamming distanceHamming distance
In information theory, the Hamming distance between two strings of equal length is the number of positions at which the corresponding symbols are different...
to
 is no more than
is no more than 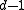 . Similarly,
. Similarly, 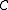 with (minimum) distance
with (minimum) distance 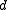 has the following properties:
has the following properties:
-
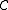 can detect
can detect 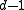 errors : Because a codeword
errors : Because a codeword  is the only codeword in the Hamming ball centered at itself with radius
is the only codeword in the Hamming ball centered at itself with radius 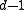 , no error pattern of
, no error pattern of  or fewer errors could change one codeword to another. When the receiver detects that the received vector is not a codeword of
or fewer errors could change one codeword to another. When the receiver detects that the received vector is not a codeword of 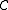 , the errors are detected (but no guarantee to correct).
, the errors are detected (but no guarantee to correct). -
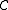 can correct
can correct  errors. Because a codeword
errors. Because a codeword  is the only codeword in the Hamming ball centered at itself with radius
is the only codeword in the Hamming ball centered at itself with radius  , the two Hamming balls centered at two different codewords respectively with both radius
, the two Hamming balls centered at two different codewords respectively with both radius 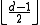 do not overlap with each other. Therefore, if we consider the error correction as finding the codeword closest to the received word
do not overlap with each other. Therefore, if we consider the error correction as finding the codeword closest to the received word 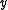 , as long as the number of errors is no more than
, as long as the number of errors is no more than 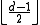 , there is only one codeword in the hamming ball centered at
, there is only one codeword in the hamming ball centered at 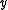 with radius
with radius  , therefore all errors could be corrected.
, therefore all errors could be corrected. - In order to decode in the presence of more than
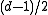 errors, list-decoding or maximum likelihood decoding can be used.
errors, list-decoding or maximum likelihood decoding can be used. -
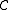 can correct
can correct 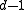 erasuresBinary erasure channelA binary erasure channel is a common communications channel model used in coding theory and information theory. In this model, a transmitter sends a bit , and the receiver either receives the bit or it receives a message that the bit was not received...
erasuresBinary erasure channelA binary erasure channel is a common communications channel model used in coding theory and information theory. In this model, a transmitter sends a bit , and the receiver either receives the bit or it receives a message that the bit was not received...
. By erasure it means that the position of the erased symbol is known. Correcting could be achieved by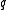 -passing decoding : In
-passing decoding : In 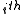 passing the erased position is filled with the
passing the erased position is filled with the 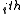 symbol and error correcting is carried out. There must be one passing that the number of errors is no more than
symbol and error correcting is carried out. There must be one passing that the number of errors is no more than 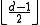 and therefore the erasures could be corrected.
and therefore the erasures could be corrected.
Lower and upper bounds of block codes
Family of codes
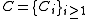 is called family of codes, where
is called family of codes, where 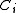 is an
is an 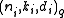 code with monotonic increasing
code with monotonic increasing 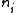 .
.Rate of family of codes
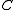 is defined as
is defined as 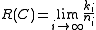
Relative distance of family of codes
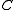 is defined as
is defined as 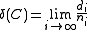
To explore the relationship between
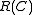 and
and 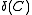 , a set of lower and upper bounds of block codes are known.
, a set of lower and upper bounds of block codes are known. Hamming boundHamming boundIn mathematics and computer science, in the field of coding theory, the Hamming bound is a limit on the parameters of an arbitrary block code: it is also known as the sphere-packing bound or the volume bound from an interpretation in terms of packing balls in the Hamming metric into the space of...
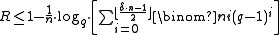
Singleton boundSingleton boundIn coding theory, the Singleton bound, named after Richard Collom Singleton, is a relatively crude bound on the size of a block code C with block length n, size r and minimum distance d.-Statement of the Bound:...
The Singleton bound is that the sum of the rate and the relative distance of a block code cannot be much larger than 1: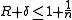 .
.In other words, every block code satisfies the inequality
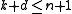 .
.Reed–Solomon codes are non-trivial examples of codes that satisfy the singleton bound with equality.
Plotkin boundPlotkin boundIn the mathematics of coding theory, the Plotkin bound, named after Morris Plotkin, is a bound on the maximum possible number of codewords in binary codes of given length n and given minimum distance d.- Statement of the bound :...
For 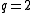 ,
, 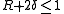
For the general case, the following Plotkin bounds holds for any
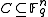 with distance
with distance 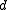 :
:1. If

2. If
 >
> 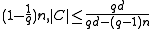
For any
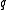 -ary code with distance
-ary code with distance  ,
, 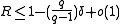
Gilbert–Varshamov boundGilbert-Varshamov boundIn coding theory, the Gilbert–Varshamov bound is a bound on the parameters of a code . It is occasionally known as the Gilbert–Shannon–Varshamov bound , but the Gilbert–Varshamov bound is by far the most popular name...
 , where
, where 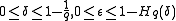 ,
,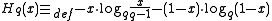 is the
is the 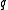 -ary entropy function.
-ary entropy function.Johnson bound
Define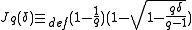 .
. Let
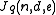 be the maximum number of codewords in a Hamming ball of radius
be the maximum number of codewords in a Hamming ball of radius  for any code
for any code  of distance
of distance 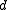 .
.Then we have the Johnson Bound :
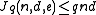 , if
, if 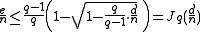
Elias–Bassalygo bound
Sphere packings and lattices
Block codes are tied to the sphere packing problem which has received some attention over the years. In two dimensions, it is easy to visualize. Take a bunch of pennies flat on the table and push them together. The result is a hexagon pattern like a bee's nest. But block codes rely on more dimensions which cannot easily be visualized. The powerful Golay codeBinary Golay code
In mathematics and electronics engineering, a binary Golay code is a type of error-correcting code used in digital communications. The binary Golay code, along with the ternary Golay code, has a particularly deep and interesting connection to the theory of finite sporadic groups in mathematics....
used in deep space communications uses 24 dimensions. If used as a binary code (which it usually is), the dimensions refer to the length of the codeword as defined above.
The theory of coding uses the N-dimensional sphere model. For example, how many pennies can be packed into a circle on a tabletop or in 3 dimensions, how many marbles can be packed into a globe. Other considerations enter the choice of a code. For example, hexagon packing into the constraint of a rectangular box will leave empty space at the corners. As the dimensions get larger, the percentage of empty space grows smaller. But at certain dimensions, the packing uses all the space and these codes are the so called perfect codes. There are very few of these codes.
Another property is the number of neighbors a single codeword may have.
Again, consider pennies as an example. First we pack the pennies in a rectangular grid. Each penny will have 4 near neighbors (and 4 at the corners which are farther away). In a hexagon, each penny will have 6 near neighbors. Respectively, in three and four dimensions, the maximum packing is given by the 12-face and 24-cell with 12 and 24 neighbors, respectively. When we increase the dimensions, the number of near neighbors increases very rapidly. In general, the value is given by the kissing numbers.
The result is the number of ways for noise to make the receiver choose
a neighbor (hence an error) grows as well. This is a fundamental limitation
of block codes, and indeed all codes. It may be harder to cause an error to
a single neighbor, but the number of neighbors can be large enough so the
total error probability actually suffers.
See also
- Channel CapacityChannel capacityIn electrical engineering, computer science and information theory, channel capacity is the tightest upper bound on the amount of information that can be reliably transmitted over a communications channel...
- Shannon–Hartley theoremShannon–Hartley theoremIn information theory, the Shannon–Hartley theorem tells the maximum rate at which information can be transmitted over a communications channel of a specified bandwidth in the presence of noise. It is an application of the noisy channel coding theorem to the archetypal case of a continuous-time...
- Noisy channel
- List decoding
- Sphere packingSphere packingIn geometry, a sphere packing is an arrangement of non-overlapping spheres within a containing space. The spheres considered are usually all of identical size, and the space is usually three-dimensional Euclidean space...