Binary Golay code
Encyclopedia
In mathematics
and electronics engineering, a binary Golay code is a type of error-correcting code used in digital communications. The binary Golay code, along with the ternary Golay code
, has a particularly deep and interesting connection to the theory of finite sporadic groups in mathematics. These codes are named in honor of Marcel J. E. Golay
.
There are two closely related binary Golay codes. The extended binary Golay code encodes 12 bits of data in a 24-bit word in such a way that any 3-bit errors can be corrected and any 7-bit errors can be detected.
The other, the perfect binary Golay code, has codewords of length 23 and is obtained from the extended binary Golay code by deleting one coordinate position (conversely, the extended binary Golay code is obtained from the perfect binary Golay code by adding a parity bit
). In standard code notation the codes have parameters [24, 12, 8] and [23, 12, 7].
W of the space V=F224 of 24-bit words such that any two distinct elements of W differ in at least eight coordinates. Equivalently, any non-zero element of W has at least eight non-zero coordinates.
The perfect binary Golay code is a perfect code. That is, the spheres of radius three around code words form a partition of the vector space.
The automorphism group of the binary Golay code is the Mathieu group
.
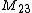The automorphism group of the extended binary Golay code is the Mathieu group
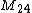. The other Mathieu groups occur as stabilizer
s of one or several elements of W.
The Golay code word
s of weight eight are elements of the S(5,8,24) Steiner system
.
1 & 2 spacecraft needed to transmit hundreds of color pictures of Jupiter
and Saturn
in their 1979, 1980, and 1981 fly-bys within a constrained telecommunications bandwidth.
(ALE) in High Frequency
(HF) radio systems specifies the use of an extended (24,12) Golay block code for forward error correction
(FEC).
The minimum Hamming distance
between any two code words (the number of bits by which any pair of code words differs) is eight.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
and electronics engineering, a binary Golay code is a type of error-correcting code used in digital communications. The binary Golay code, along with the ternary Golay code
Ternary Golay code
There are two closely related error-correcting codes known as ternary Golay codes. The code generally known simply as the ternary Golay code is a perfect [11, 6, 5] ternary linear code; the extended ternary Golay code is a [12, 6, 6] linear code obtained by adding a zero-sum check digit to the...
, has a particularly deep and interesting connection to the theory of finite sporadic groups in mathematics. These codes are named in honor of Marcel J. E. Golay
Marcel J. E. Golay
Marcel J.E. Golay was a Swiss-born mathematician, physicist, and information theorist, who applied mathematics to real-world military and industrial problems. He was born in Neuchâtel, Switzerland.-Career:...
.
There are two closely related binary Golay codes. The extended binary Golay code encodes 12 bits of data in a 24-bit word in such a way that any 3-bit errors can be corrected and any 7-bit errors can be detected.
The other, the perfect binary Golay code, has codewords of length 23 and is obtained from the extended binary Golay code by deleting one coordinate position (conversely, the extended binary Golay code is obtained from the perfect binary Golay code by adding a parity bit
Parity bit
A parity bit is a bit that is added to ensure that the number of bits with the value one in a set of bits is even or odd. Parity bits are used as the simplest form of error detecting code....
). In standard code notation the codes have parameters [24, 12, 8] and [23, 12, 7].
Mathematical definition
In mathematical terms, the extended binary Golay code consists of a 12-dimensional subspaceLinear subspace
The concept of a linear subspace is important in linear algebra and related fields of mathematics.A linear subspace is usually called simply a subspace when the context serves to distinguish it from other kinds of subspaces....
W of the space V=F224 of 24-bit words such that any two distinct elements of W differ in at least eight coordinates. Equivalently, any non-zero element of W has at least eight non-zero coordinates.
- The possible sets of non-zero coordinates as w ranges over W are called code words. In the extended binary Golay code, all code words have the Hamming weightHamming weightThe Hamming weight of a string is the number of symbols that are different from the zero-symbol of the alphabet used. It is thus equivalent to the Hamming distance from the all-zero string of the same length. For the most typical case, a string of bits, this is the number of 1's in the string...
s of 0, 8, 12, 16, or 24. - Up to relabeling coordinates, W is unique.
The perfect binary Golay code is a perfect code. That is, the spheres of radius three around code words form a partition of the vector space.
The automorphism group of the binary Golay code is the Mathieu group
Mathieu group
In the mathematical field of group theory, the Mathieu groups, named after the French mathematician Émile Léonard Mathieu, are five finite simple groups he discovered and reported in papers in 1861 and 1873; these were the first sporadic simple groups discovered...
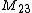.The automorphism group of the extended binary Golay code is the Mathieu group
Mathieu group
In the mathematical field of group theory, the Mathieu groups, named after the French mathematician Émile Léonard Mathieu, are five finite simple groups he discovered and reported in papers in 1861 and 1873; these were the first sporadic simple groups discovered...
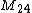. The other Mathieu groups occur as stabilizerGroup action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
s of one or several elements of W.
The Golay code word
Code word
In communication, a code word is an element of a standardized code or protocol. Each code word is assembled in accordance with the specific rules of the code and assigned a unique meaning...
s of weight eight are elements of the S(5,8,24) Steiner system
Steiner system
250px|right|thumbnail|The [[Fano plane]] is an S Steiner triple system. The blocks are the 7 lines, each containing 3 points. Every pair of points belongs to a unique line....
.
Constructions
- Lexicographic code: Order the vectors in V lexicographically (i.e., interpret them as unsigned 24-bit binary integers and take the usual ordering). Starting with w1 = 0, define w2, w3, ..., w12 by the rule that wn is the smallest integer which differs from all linear combinations of previous elements in at least eight coordinates. Then W can be defined as the span of w1, ..., w12.
- Quadratic residue codeQuadratic residue codeA quadratic residue code is a type of cyclic code.There is a quadratic residue code of length pover the finite field GF whenever pand l are primes, p is odd andl is a quadratic residue modulo p....
: Consider the set N of quadratic non-residues (mod 23). This is an 11-element subset of the cyclic groupCyclic groupIn group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
Z/23Z. Consider the translates t+N of this subset. Augment each translate to a 12-element set St by adding an element ∞. Then labeling the basis elements of V by 0, 1, 2, ..., 22, ∞, W can be defined as the span of the words St together with the word consisting of all basis vectors. (The perfect code is obtained by leaving out ∞.) - As a Cyclic code: The perfect G23 code can be constructed via factorization of
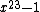, it is the code generated by 
- The Miracle Octad GeneratorMiracle Octad GeneratorIn mathematics, the Miracle Octad Generator, or MOG, is a mathematical tool introduced by for manipulating the Mathieu groups, binary Golay code and Leech lattice.-Description:...
of R. T. Curtis: This uses a 4×6 array of square cells to picture the 759 Hamming-weight-8 code words, or "octads," of the extended binary Golay code. The remaining code words are obtained via symmetric differenceSymmetric differenceIn mathematics, the symmetric difference of two sets is the set of elements which are in either of the sets and not in their intersection. The symmetric difference of the sets A and B is commonly denoted by A\,\Delta\,B\,orA \ominus B....
s of subsets of the 24 cells-- i.e., by binary addition. - Winning positions in the mathematical gameMathematical gameA mathematical game is a multiplayer game whose rules, strategies, and outcomes can be studied and explained by mathematics. Examples of such games are Tic-tac-toe and Dots and Boxes, to name a couple. On the surface, a game need not seem mathematical or complicated to still be a mathematical game...
of Mogul: a position in Mogul is a row of 24 coins. Each turn consists of flipping from one to seven coins such that the leftmost of the flipped coins goes from head to tail. The losing positions are those with no legal move. If heads are interpreted as 1 and tails as 0 then moving to a codeword from the extended binary Golay code guarantees it will be possible to force a win. - A generator matrixGenerator matrixIn coding theory, a generator matrix is a basis for a linear code, generating all its possible codewords.If the matrix is G and the linear code is C,where w is a codeword of the linear code C, c is a row vector, and a bijection exists between w and c. A generator matrix for an q-code has...
for the binary Golay code is I A, where I is the 12×12 identity matrix, and A is the complement of the adjacency matrixAdjacency matrixIn mathematics and computer science, an adjacency matrix is a means of representing which vertices of a graph are adjacent to which other vertices...
of the icosahedronIcosahedronIn geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids....
.
NASA Deep Space Missions
The VoyagerVoyager program
The Voyager program is a U.S program that launched two unmanned space missions, scientific probes Voyager 1 and Voyager 2. They were launched in 1977 to take advantage of a favorable planetary alignment of the late 1970s...
1 & 2 spacecraft needed to transmit hundreds of color pictures of Jupiter
Jupiter
Jupiter is the fifth planet from the Sun and the largest planet within the Solar System. It is a gas giant with mass one-thousandth that of the Sun but is two and a half times the mass of all the other planets in our Solar System combined. Jupiter is classified as a gas giant along with Saturn,...
and Saturn
Saturn
Saturn is the sixth planet from the Sun and the second largest planet in the Solar System, after Jupiter. Saturn is named after the Roman god Saturn, equated to the Greek Cronus , the Babylonian Ninurta and the Hindu Shani. Saturn's astronomical symbol represents the Roman god's sickle.Saturn,...
in their 1979, 1980, and 1981 fly-bys within a constrained telecommunications bandwidth.
- Color image transmission required three times the amount of data, so the Golay (24,12,8) code was used.
- This Golay code is only triple-error correcting, but it could be transmitted at a much higher data rate than the Hadamard codeHadamard codeThe Hadamard code is an error-correcting code that is used for error detection and correction when transmitting messages over very noisy or unreliable channels....
that was used during the Mariner mission.
ALE HF data communications
The new American government standards for automatic link establishmentAutomatic link establishment
Automatic Link Establishment, commonly known as ALE, is the worldwide de facto standard for digitally initiating and sustaining HF radio communications. ALE is a feature in an HF communications radio transceiver system, that enables the radio station to make contact, or initiate a circuit, between...
(ALE) in High Frequency
High frequency
High frequency radio frequencies are between 3 and 30 MHz. Also known as the decameter band or decameter wave as the wavelengths range from one to ten decameters . Frequencies immediately below HF are denoted Medium-frequency , and the next higher frequencies are known as Very high frequency...
(HF) radio systems specifies the use of an extended (24,12) Golay block code for forward error correction
Forward error correction
In telecommunication, information theory, and coding theory, forward error correction or channel coding is a technique used for controlling errors in data transmission over unreliable or noisy communication channels....
(FEC).
- The Extended (24,12) Golay Code specified is a (24,12) block code.
- This code encodes 12 data bits to produce 24-bit code words.
- It is furthermore a systematic code, meaning that the 12 data bits are present in unchanged form in the code word.
The minimum Hamming distance
Hamming distance
In information theory, the Hamming distance between two strings of equal length is the number of positions at which the corresponding symbols are different...
between any two code words (the number of bits by which any pair of code words differs) is eight.