Weighing matrix
Encyclopedia
In mathematics
, a weighing matrix W of order n with weight w is an n × n
-matrix such that 
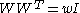. A weighing matrix is also called a weighing design.
For convenience, a weighing matrix of order
and weight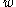 
is often denoted by 
.
A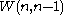
is equivalent to a conference matrix
and a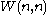
is an Hadamard matrix
.
Some properties are immediate from the definition:
Example of W(2, 2):
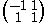
The main question about weighing matrices is their existence: for which values of n and w does there exist a W(n,w)? A great deal about this is unknown. An equally important but often overlooked question about weighing matrices is their enumeration: for a given n and w, how many W(n,w)'s are there? More deeply, one may ask for a classification in terms of structure, but this is far beyond our power at present, even for Hadamard or conference matrices.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a weighing matrix W of order n with weight w is an n × n
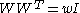-matrix such that . A weighing matrix is also called a weighing design.For convenience, a weighing matrix of order
and weight 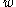is often denoted by .A
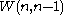is equivalent to a conference matrixConference matrix
In mathematics, a conference matrix is a square matrix C with 0 on the diagonal and +1 and −1 off the diagonal, such that CTC is a multiple of the identity matrix I...
and a
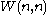is an Hadamard matrixHadamard matrix
In mathematics, an Hadamard matrix, named after the French mathematician Jacques Hadamard, is a square matrix whose entries are either +1 or −1 and whose rows are mutually orthogonal...
.
Some properties are immediate from the definition:
- The rows are pairwise orthogonal.
- Each row and each column has exactly
non-zero elements. -
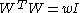, since the definition means that 
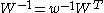(assuming the weight is not 0).
Example of W(2, 2):
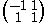
The main question about weighing matrices is their existence: for which values of n and w does there exist a W(n,w)? A great deal about this is unknown. An equally important but often overlooked question about weighing matrices is their enumeration: for a given n and w, how many W(n,w)'s are there? More deeply, one may ask for a classification in terms of structure, but this is far beyond our power at present, even for Hadamard or conference matrices.
External links
- On Hotelling's Weighing Problem, Alexander M. Mood, Ann. Math. Statist. Volume 17, Number 4 (1946), 432-446.