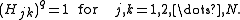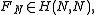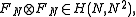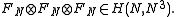Butson-type Hadamard matrices
Encyclopedia
In mathematics, a complex Hadamard matrix
H of size N with all its columns (rows) mutually orthogonal, belongs to the Butson-type H(q, N) if all its elements are powers of q-th root of unity,
then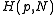 can exist
can exist
only for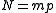 with integer m and
with integer m and
it is conjectured they exist for all such cases
with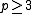 .
.
In general, the problem of finding all sets
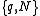 such that the Butson - type matrices
such that the Butson - type matrices
 exist, remains open.
exist, remains open.
Hadamard matrix
In mathematics, an Hadamard matrix, named after the French mathematician Jacques Hadamard, is a square matrix whose entries are either +1 or −1 and whose rows are mutually orthogonal...
H of size N with all its columns (rows) mutually orthogonal, belongs to the Butson-type H(q, N) if all its elements are powers of q-th root of unity,
Existence
If p is primePrime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
then
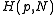 can exist
can existonly for
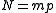 with integer m and
with integer m andit is conjectured they exist for all such cases
with
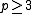 .
.In general, the problem of finding all sets
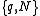 such that the Butson - type matrices
such that the Butson - type matrices exist, remains open.
exist, remains open.Examples
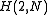 contains real Hadamard matrices of size N,
contains real Hadamard matrices of size N,
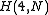 contains Hadamard matrices composed of
contains Hadamard matrices composed of 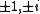 - such matrices were called by Turyn, complex Hadamard matrices.
- such matrices were called by Turyn, complex Hadamard matrices.
- in the limit
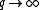 one can approximate all complex Hadamard matrices.
one can approximate all complex Hadamard matrices.
- Fourier matrices
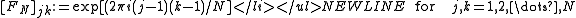
belong to the Butson-type,
- while
-
-
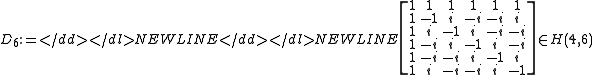
-
-
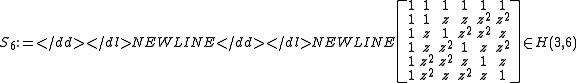 , where
, where 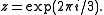
External links
- Complex Hadamard Matrices of Butson type - a catalogue, by Wojciech Bruzda, Wojciech Tadej and Karol Życzkowski, retrieved October 24, 2006
-
-
-
-