
Nonassociative ring
Encyclopedia
In abstract algebra
, a nonassociative ring is a generalization of the concept of ring
.
A nonassociative ring is a set R with two operations, addition and multiplication, such that:
Unlike for rings, we do not require multiplication to satisfy associativity
. We also do not require the presence of a unit, an element 1 such that .
.
In this context, nonassociative means that multiplication is not required to be associative, but associative multiplication is permitted. Thus rings, which we'll call associative rings for clarity, are a special case of nonassociative rings.
Some classes of nonassociative rings replace associative laws with different constraints on the order of application of multiplication. For example Lie ring
s and Lie algebra
s replace the associative law with the Jacobi identity
, while Jordan rings and Jordan algebra
s replace the associative law with the Jordan identity.
s, constructed by John T. Graves
in 1843, were the first example of a ring that is not associative.
The hyperbolic quaternion
s of Alexander Macfarlane
(1891) form a nonassociative ring that suggested the mathematical footing for spacetime theory that followed later.
Other examples of nonassociative rings include the following:
For example, for a nonassociative ring with an identity element:
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, a nonassociative ring is a generalization of the concept of ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
.
A nonassociative ring is a set R with two operations, addition and multiplication, such that:
- R is an abelian groupAbelian groupIn abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
under addition:-

-
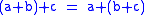
- There exists 0 in R such that
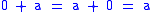
- For each a in R, there exists an element -a such that
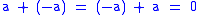
-
- Multiplication is linear in each variable:
-
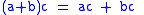 (left distributive law)
(left distributive law) -
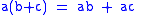 (right distributive law)
(right distributive law)
-
Unlike for rings, we do not require multiplication to satisfy associativity
Associativity
In mathematics, associativity is a property of some binary operations. It means that, within an expression containing two or more occurrences in a row of the same associative operator, the order in which the operations are performed does not matter as long as the sequence of the operands is not...
. We also do not require the presence of a unit, an element 1 such that
 .
.In this context, nonassociative means that multiplication is not required to be associative, but associative multiplication is permitted. Thus rings, which we'll call associative rings for clarity, are a special case of nonassociative rings.
Some classes of nonassociative rings replace associative laws with different constraints on the order of application of multiplication. For example Lie ring
Lie ring
In mathematics a Lie ring is a structure related to Lie algebras that can arise as a generalisation of Lie algebras, or through the study of the lower central series of groups.- Formal definition :...
s and Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
s replace the associative law with the Jacobi identity
Jacobi identity
In mathematics the Jacobi identity is a property that a binary operation can satisfy which determines how the order of evaluation behaves for the given operation. Unlike for associative operations, order of evaluation is significant for operations satisfying Jacobi identity...
, while Jordan rings and Jordan algebra
Jordan algebra
In abstract algebra, a Jordan algebra is an algebra over a field whose multiplication satisfies the following axioms:# xy = yx # = x ....
s replace the associative law with the Jordan identity.
Examples
The octonionOctonion
In mathematics, the octonions are a normed division algebra over the real numbers, usually represented by the capital letter O, using boldface O or blackboard bold \mathbb O. There are only four such algebras, the other three being the real numbers R, the complex numbers C, and the quaternions H...
s, constructed by John T. Graves
John T. Graves
John Thomas Graves was an Irish jurist and mathematician. He was a friend of William Rowan Hamilton, and is credited both with inspiring Hamilton to discover the quaternions and with personally discovering the octonions, which he called the octaves...
in 1843, were the first example of a ring that is not associative.
The hyperbolic quaternion
Hyperbolic quaternion
In the abstract algebra of algebras over a field, the hyperbolic quaternionq = a + bi + cj + dk, \quad a,b,c,d \in R \!is a mutated quaternion wherei^2 = j^2 = k^2 = +1 \! instead of the usual −1....
s of Alexander Macfarlane
Alexander Macfarlane
Alexander Macfarlane was a Nova Scotia lawyer and political figure. He was a member of the Canadian Senate from 1870 to 1898. His surname also appears as McFarlane in some sources....
(1891) form a nonassociative ring that suggested the mathematical footing for spacetime theory that followed later.
Other examples of nonassociative rings include the following:
- (R3, +, × ) where × is the cross productCross productIn mathematics, the cross product, vector product, or Gibbs vector product is a binary operation on two vectors in three-dimensional space. It results in a vector which is perpendicular to both of the vectors being multiplied and normal to the plane containing them...
of vectors in 3-space - The Cayley–Dickson construction provides an infinite family of nonassociative rings.
- Lie algebraLie algebraIn mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
s and Lie ringLie ringIn mathematics a Lie ring is a structure related to Lie algebras that can arise as a generalisation of Lie algebras, or through the study of the lower central series of groups.- Formal definition :...
s - Jordan algebraJordan algebraIn abstract algebra, a Jordan algebra is an algebra over a field whose multiplication satisfies the following axioms:# xy = yx # = x ....
s and Jordan rings. - Alternative rings: A nonassociative ring R is said to be an alternative ring if [x,x,y]=[y,x,x]=0, where [x,y,z] = (xy)z - x(yz) is the associatorAssociatorIn abstract algebra, the term associator is used in different ways as a measure of the nonassociativity of an algebraic structure.-Ring theory:...
.
Properties
Most elementary properties of rings fail in the absence of associativity.For example, for a nonassociative ring with an identity element:
- If an element
 has left and right multiplicative inverses,
has left and right multiplicative inverses, 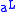 and
and 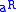 , then
, then 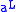 and
and 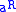 can be distinct.
can be distinct. - Elements with multiplicative inverses can still be zero divisorZero divisorIn abstract algebra, a nonzero element a of a ring is a left zero divisor if there exists a nonzero b such that ab = 0. Similarly, a nonzero element a of a ring is a right zero divisor if there exists a nonzero c such that ca = 0. An element that is both a left and a right zero divisor is simply...
s.

