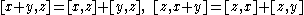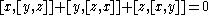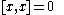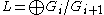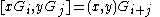Lie ring
Encyclopedia
In mathematics
a Lie ring is a structure related to Lie algebra
s that can arise as a generalisation of Lie algebras, or through the study of the lower central series of groups
.
with multiplication that is anticommutative and satisfies the Jacobi identity
. More specifically we can define a Lie ring to be an abelian group
to be an abelian group
with an operation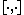 that has the following properties:
that has the following properties:
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
a Lie ring is a structure related to Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
s that can arise as a generalisation of Lie algebras, or through the study of the lower central series of groups
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
.
Formal definition
A Lie ring is defined as a nonassociative ringNonassociative ring
In abstract algebra, a nonassociative ring is a generalization of the concept of ring.A nonassociative ring is a set R with two operations, addition and multiplication, such that:# R is an abelian group under addition:## a+b = b+a...
with multiplication that is anticommutative and satisfies the Jacobi identity
Jacobi identity
In mathematics the Jacobi identity is a property that a binary operation can satisfy which determines how the order of evaluation behaves for the given operation. Unlike for associative operations, order of evaluation is significant for operations satisfying Jacobi identity...
. More specifically we can define a Lie ring
 to be an abelian group
to be an abelian groupAbelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
with an operation
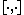 that has the following properties:
that has the following properties:- Bilinearity:
- for all x, y, z ∈ L.
- The Jacobi identity:
- for all x, y, z in L.
- For all x in L.
Examples
- Any Lie algebraLie algebraIn mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
over a general ringRing (mathematics)In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
instead of a fieldField (mathematics)In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
is an example of a Lie ring. Lie rings are not Lie groupLie groupIn mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
s under addition, despite the name.
- Any associative ring can be made into a Lie ring by defining a bracket operator
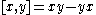 .
.
- For an example of a Lie ring arising from the study of groupsGroup (mathematics)In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
, let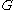 be a group with
be a group with 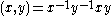 the commutator operation, and let
the commutator operation, and let 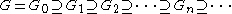 be a central seriesCentral seriesIn mathematics, especially in the fields of group theory and Lie theory, a central series is a kind of normal series of subgroups or Lie subalgebras, expressing the idea that the commutator is nearly trivial...
be a central seriesCentral seriesIn mathematics, especially in the fields of group theory and Lie theory, a central series is a kind of normal series of subgroups or Lie subalgebras, expressing the idea that the commutator is nearly trivial...
in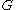 — that is the commutator subgroup
— that is the commutator subgroup 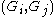 is contained in
is contained in 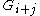 for any
for any  . Then
. Then
- is a Lie ring with addition supplied by the group operation (which will be commutative in each homogeneous part), and the bracket operation given by
- extended linearly. Note that the centrality of the series ensures the commutator
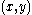 gives the bracket operation the appropriate Lie theoretic properties.
gives the bracket operation the appropriate Lie theoretic properties.