Niemeier lattice
Encyclopedia
In mathematics
, a Niemeier lattice is one of the 24
positive definite
even unimodular lattice
s of rank
24,
which were classified by . gave a simplified proof of the classification. has a sentence mentioning that he found more than 10 such lattices, but gives no further details. One example of a Niemeier lattice is the Leech lattice
.
root system
s. These Dynkin diagrams have rank either 0 or 24, and all of their components have the same Coxeter number
. (The Coxeter number, at least in these cases, is
the number of roots divided by the dimension.) There are exactly 24 Dynkin diagrams with these properties, and there turns out to be a unique Niemeier
lattice for each of these Dynkin diagrams.
The complete list of Niemeier lattices is given in the following table.
In the table,
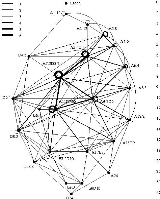
Each point represents one of the 24 Niemeier lattices, and the lines joining them represent the 24 dimensional odd unimodular lattices with no norm 1 vectors. (Thick lines represent multiple lines.) The number on the right is the Coxeter number of the Niemeier lattice.
In 32 dimensions the neighborhood graph has more than a billion vertices.
The Leech lattice is acted on by a double cover of the Conway group
,
and the lattices A124 and A212
are acted on by the Mathieu group
s M24 and M12.
The Niemeier lattices, other than the Leech lattice, correspond to
the deep holes of the Leech lattice. This implies that the affine Dynkin diagrams of the Niemeier lattices can be seen inside the Leech lattice, when
two points of the Leech lattice are joined by no lines when they have distance
 , by 1 line if they have distance
, by 1 line if they have distance  ,
,
and by a double line if they have distance .
.
Niemeier lattices also correspond to the 24 orbits of primitive norm zero vectors of the even unimodular Lorentzian lattice II25,1
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a Niemeier lattice is one of the 24
positive definite
Definite bilinear form
In mathematics, a definite bilinear form is a bilinear form B over some vector space V such that the associated quadratic formQ=B \,...
even unimodular lattice
Unimodular lattice
In mathematics, a unimodular lattice is a lattice of determinant 1 or −1.The E8 lattice and the Leech lattice are two famous examples.- Definitions :...
s of rank
Rank of an abelian group
In mathematics, the rank, Prüfer rank, or torsion-free rank of an abelian group A is the cardinality of a maximal linearly independent subset. The rank of A determines the size of the largest free abelian group contained in A. If A is torsion-free then it embeds into a vector space over the...
24,
which were classified by . gave a simplified proof of the classification. has a sentence mentioning that he found more than 10 such lattices, but gives no further details. One example of a Niemeier lattice is the Leech lattice
Leech lattice
In mathematics, the Leech lattice is an even unimodular lattice Λ24 in 24-dimensional Euclidean space E24 found by .-History:Many of the cross-sections of the Leech lattice, including the Coxeter–Todd lattice and Barnes–Wall lattice, in 12 and 16 dimensions, were found much earlier than...
.
Classification
Niemeier lattices are usually labeled by the Dynkin diagram of theirroot system
Root system
In mathematics, a root system is a configuration of vectors in a Euclidean space satisfying certain geometrical properties. The concept is fundamental in the theory of Lie groups and Lie algebras...
s. These Dynkin diagrams have rank either 0 or 24, and all of their components have the same Coxeter number
Coxeter number
In mathematics, the Coxeter number h is the order of a Coxeter element of an irreducible Coxeter group, hence also of a root system or its Weyl group. It is named after H.S.M. Coxeter.-Definitions:...
. (The Coxeter number, at least in these cases, is
the number of roots divided by the dimension.) There are exactly 24 Dynkin diagrams with these properties, and there turns out to be a unique Niemeier
lattice for each of these Dynkin diagrams.
The complete list of Niemeier lattices is given in the following table.
In the table,
- G0 is the order of the group generated by reflections
- G1 is the order of the group of automorphisms fixing all components of the Dynkin diagram
- G2 is the order of the group of automorphisms of permutations of components of the Dynkin diagram
- G∞ is the index of the root lattice in the Niemeier lattice, in other words the order of the "glue code". It is the square root of the discriminant of the root lattice.
- G0×G1×G2 is the order of the automorphism group of the lattice
- G∞×G1×G2 is the order of the automorphism group of the corresponding deep hole.
| Lattice root system | Coxeter number | G0 | G1 | G2 | G∞ |
|---|---|---|---|---|---|
| Leech (no roots) | 0 | 1 | 2Co1 Conway group In mathematics, the Conway groups Co1, Co2, and Co3 are three sporadic groups discovered by John Horton Conway.The largest of the Conway groups, Co1, of order... |
1 | Z24 |
| A124 | 2 | 224 | 1 | M24 Mathieu group In the mathematical field of group theory, the Mathieu groups, named after the French mathematician Émile Léonard Mathieu, are five finite simple groups he discovered and reported in papers in 1861 and 1873; these were the first sporadic simple groups discovered... |
212 |
| A212 | 3 | 3!12 | 2 | M12 Mathieu group In the mathematical field of group theory, the Mathieu groups, named after the French mathematician Émile Léonard Mathieu, are five finite simple groups he discovered and reported in papers in 1861 and 1873; these were the first sporadic simple groups discovered... |
36 |
| A38 | 4 | 4!8 | 2 | 1344 | 44 |
| A46 | 5 | 5!6 | 2 | 120 | 53 |
| A54D4 | 6 | 6!4(234!) | 2 | 24 | 72 |
| D46 | 6 | (234!)6 | 3 | 720 | 43 |
| A64 | 7 | 7!4 | 2 | 12 | 72 |
| A72D52 | 8 | 8!4 (245!)4 | 2 | 4 | 32 |
| A83 | 9 | 9!3 | 2 | 6 | 27 |
| A92D6 | 10 | 10!2 (256!) | 2 | 2 | 20 |
| D64 | 10 | (256!)4 | 1 | 24 | 16 |
| E64 | 12 | (27345)4 | 2 | 24 | 9 |
| A11D7E6 | 12 | 12!(267!)(27345) | 2 | 1 | 12 |
| A122 | 13 | (13!)2 | 2 | 2 | 13 |
| D83 | 14 | (278!)3 | 1 | 6 | 8 |
| A15D9 | 16 | 16!(289!) | 2 | 1 | 8 |
| A17E7 | 18 | 18!(210345.7) | 2 | 1 | 6 |
| D10E72 | 18 | (2910!)(210345.7)2 | 1 | 2 | 4 |
| D122 | 22 | (21112!)2 | 1 | 2 | 4 |
| A24 | 25 | 25! | 1 | 2 | 5 |
| D16E8 | 30 | (21516!)(21435527) | 1 | 1 | 2 |
| E83 | 30 | (21435527)3 | 1 | 6 | 1 |
| D24 | 46 | 22324! | 1 | 1 | 2 |
The neighborhood graph of the Niemeier lattices
If L is an odd unimodular lattice of dimension 8n and M its sublattice of even vectors, then M is contained in exactly 3 unimodular lattices, one of which is L and the other two of which are even. (If L has a norm 1 vector then the two even lattices are isomorphic.) The Kneser neighborhood graph in 8n dimensions has a point for each even lattice, and a line joining two points for each odd 8n dimensional lattice with no norm 1 vectors, where the vertices of each line are the two even lattices associated to the odd lattice. There may be several lines between the same pair of vertices, and there may be lines from a vertex to itself. Kneser proved that this graph is always connected. In 8 dimensions it has one point and no lines, in 16 dimensions it has two points joined by one line, and in 24 dimensions it is the following graph:Each point represents one of the 24 Niemeier lattices, and the lines joining them represent the 24 dimensional odd unimodular lattices with no norm 1 vectors. (Thick lines represent multiple lines.) The number on the right is the Coxeter number of the Niemeier lattice.
In 32 dimensions the neighborhood graph has more than a billion vertices.
Properties
Some of the Niemeier lattices are related to sporadic simple groups.The Leech lattice is acted on by a double cover of the Conway group
Conway group
In mathematics, the Conway groups Co1, Co2, and Co3 are three sporadic groups discovered by John Horton Conway.The largest of the Conway groups, Co1, of order...
,
and the lattices A124 and A212
are acted on by the Mathieu group
Mathieu group
In the mathematical field of group theory, the Mathieu groups, named after the French mathematician Émile Léonard Mathieu, are five finite simple groups he discovered and reported in papers in 1861 and 1873; these were the first sporadic simple groups discovered...
s M24 and M12.
The Niemeier lattices, other than the Leech lattice, correspond to
the deep holes of the Leech lattice. This implies that the affine Dynkin diagrams of the Niemeier lattices can be seen inside the Leech lattice, when
two points of the Leech lattice are joined by no lines when they have distance
 , by 1 line if they have distance
, by 1 line if they have distance  ,
,and by a double line if they have distance
 .
.Niemeier lattices also correspond to the 24 orbits of primitive norm zero vectors of the even unimodular Lorentzian lattice II25,1
II25,1
In mathematics, II25,1 is the even 26-dimensional Lorentzian unimodular lattice. It has several unusual properties, arising from Conway's discovery that it has a norm zero Weyl vector...
.

