
Kissing number problem
Encyclopedia
In geometry
, a kissing number is defined as the number of non-overlapping unit spheres that touch another given unit sphere. For a lattice
packing the kissing number is the same for every sphere, but for an arbitrary sphere packing
the kissing number may vary from one sphere to another. Other names for kissing number that have been used are Newton number (after the originator of the problem), and contact number.
The kissing number problem seeks the maximum possible kissing number for n-dimensional Euclidean space
as a function of n.

It is easy to see (and to prove) that in two dimensions the kissing number is 6.
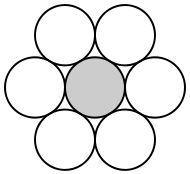
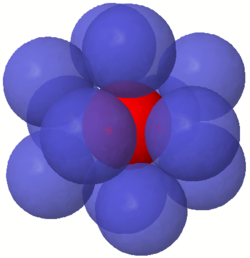 In three dimensions the kissing number is 12, but the correct value was much more difficult to establish than in dimensions one and two. It is easy to arrange 12 spheres so that each touches a central sphere, but there is a lot of space left over, and it is not obvious that there is no way to pack in a 13th sphere. (In fact, there is so much extra space that any two of the 12 outer spheres can exchange places through a continuous movement without any of the outer spheres losing contact with the center one.) This was the subject of a famous disagreement between mathematicians Isaac Newton
In three dimensions the kissing number is 12, but the correct value was much more difficult to establish than in dimensions one and two. It is easy to arrange 12 spheres so that each touches a central sphere, but there is a lot of space left over, and it is not obvious that there is no way to pack in a 13th sphere. (In fact, there is so much extra space that any two of the 12 outer spheres can exchange places through a continuous movement without any of the outer spheres losing contact with the center one.) This was the subject of a famous disagreement between mathematicians Isaac Newton
and David Gregory. Newton correctly thought that the limit was 12; Gregory thought that a 13th could fit. Some incomplete proofs that Newton was correct were offered in the nineteenth century, but the first correct proof did not appear until 1953.
In four dimensions, it was known for some time that the answer is either 24 or 25. It is easy to produce a packing of 24 spheres around a central sphere (one can place the spheres at the vertices of a suitably scaled 24-cell centered at the origin). As in the three-dimensional case, there is a lot of space left over—even more, in fact, than for n = 3—so the situation was even less clear. Finally, in 2003, Oleg Musin proved the kissing number for n = 4 to be 24, using a subtle trick.
The kissing number in n dimension
s is unknown for n > 4, except for n = 8 (240), and n = 24 (196,560). The results in these dimensions stem from the existence of highly symmetrical lattices: the E8 lattice
and the Leech lattice
.
If arrangements are restricted to regular arrangements, in which the centres of the spheres all lie on points in a lattice
, then the kissing number is known for n = 1 to 9 and n = 24 dimensions. For 5, 6 and 7 dimensions the arrangement with the highest known kissing number is the optimal lattice arrangement, but the existence of a non-lattice arrangement with a higher kissing number has not been excluded.
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, a kissing number is defined as the number of non-overlapping unit spheres that touch another given unit sphere. For a lattice
Lattice (group)
In mathematics, especially in geometry and group theory, a lattice in Rn is a discrete subgroup of Rn which spans the real vector space Rn. Every lattice in Rn can be generated from a basis for the vector space by forming all linear combinations with integer coefficients...
packing the kissing number is the same for every sphere, but for an arbitrary sphere packing
Sphere packing
In geometry, a sphere packing is an arrangement of non-overlapping spheres within a containing space. The spheres considered are usually all of identical size, and the space is usually three-dimensional Euclidean space...
the kissing number may vary from one sphere to another. Other names for kissing number that have been used are Newton number (after the originator of the problem), and contact number.
The kissing number problem seeks the maximum possible kissing number for n-dimensional Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
as a function of n.
Known greatest kissing numbers
In one dimension, the kissing number is 2:
It is easy to see (and to prove) that in two dimensions the kissing number is 6.


Isaac Newton
Sir Isaac Newton PRS was an English physicist, mathematician, astronomer, natural philosopher, alchemist, and theologian, who has been "considered by many to be the greatest and most influential scientist who ever lived."...
and David Gregory. Newton correctly thought that the limit was 12; Gregory thought that a 13th could fit. Some incomplete proofs that Newton was correct were offered in the nineteenth century, but the first correct proof did not appear until 1953.
In four dimensions, it was known for some time that the answer is either 24 or 25. It is easy to produce a packing of 24 spheres around a central sphere (one can place the spheres at the vertices of a suitably scaled 24-cell centered at the origin). As in the three-dimensional case, there is a lot of space left over—even more, in fact, than for n = 3—so the situation was even less clear. Finally, in 2003, Oleg Musin proved the kissing number for n = 4 to be 24, using a subtle trick.
The kissing number in n dimension
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
s is unknown for n > 4, except for n = 8 (240), and n = 24 (196,560). The results in these dimensions stem from the existence of highly symmetrical lattices: the E8 lattice
E8 lattice
In mathematics, the E8 lattice is a special lattice in R8. It can be characterized as the unique positive-definite, even, unimodular lattice of rank 8...
and the Leech lattice
Leech lattice
In mathematics, the Leech lattice is an even unimodular lattice Λ24 in 24-dimensional Euclidean space E24 found by .-History:Many of the cross-sections of the Leech lattice, including the Coxeter–Todd lattice and Barnes–Wall lattice, in 12 and 16 dimensions, were found much earlier than...
.
If arrangements are restricted to regular arrangements, in which the centres of the spheres all lie on points in a lattice
Lattice (group)
In mathematics, especially in geometry and group theory, a lattice in Rn is a discrete subgroup of Rn which spans the real vector space Rn. Every lattice in Rn can be generated from a basis for the vector space by forming all linear combinations with integer coefficients...
, then the kissing number is known for n = 1 to 9 and n = 24 dimensions. For 5, 6 and 7 dimensions the arrangement with the highest known kissing number is the optimal lattice arrangement, but the existence of a non-lattice arrangement with a higher kissing number has not been excluded.
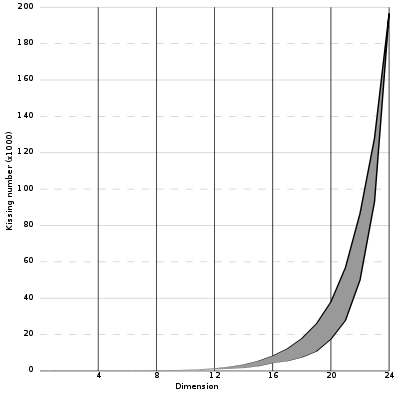
Some known bounds
The following table lists some known bounds on the kissing number in various dimensions. The dimensions in which the kissing number is known are listed in boldface.
| Dimension | Lower bound |
Upper bound |
|---|---|---|
| 1 | 2 | |
| 2 | 6 | |
| 3 | 12 Tetrahedral-octahedral honeycomb The tetrahedral-octahedral honeycomb or alternated cubic honeycomb is a space-filling tessellation in Euclidean 3-space. It is composed of alternating octahedra and tetrahedra in a ratio of 1:2.... |
|
| 4 | 24 | |
| 5 | 40 | 44 |
| 6 | 72 | 78 |
| 7 | 126 | 134 |
| 8 | 240 5 21 honeycomb In geometry, the 521 honeycomb is a uniform tessellation of 8-dimensional Euclidean space.This honeycomb was first studied by Gosset who called it a 9-ic semi-regular figure... |
|
| 9 | 306 | 364 |
| 10 | 500 | 554 |
| 11 | 582 | 870 |
| 12 | 840 | 1,357 |
| 13 | 1,154 | 2,069 |
| 14 | 1,606 | 3,183 |
| 15 | 2,564 | 4,866 |
| 16 | 4,320 | 7,355 |
| 17 | 5,346 | 11,072 |
| 18 | 7,398 | 16,572 |
| 19 | 10,688 | 24,812 |
| 20 | 17,400 | 36,764 |
| 21 | 27,720 | 54,584 |
| 22 | 49,896 | 82,340 |
| 23 | 93,150 | 124,416 |
| 24 | 196,560 Leech lattice In mathematics, the Leech lattice is an even unimodular lattice Λ24 in 24-dimensional Euclidean space E24 found by .-History:Many of the cross-sections of the Leech lattice, including the Coxeter–Todd lattice and Barnes–Wall lattice, in 12 and 16 dimensions, were found much earlier than... |
|

