List of regular polytopes
Encyclopedia
This page lists the regular polytope
s in Euclidean
, spherical
and hyperbolic
spaces.
The Schläfli symbol notation describes every regular polytope, and is used widely below as a compact reference name for each.
The regular polytopes are grouped by dimension and subgrouped by convex, nonconvex and infinite forms. Nonconvex forms use the same vertices as the convex forms, but have intersecting facets
. Infinite forms tessellate
a one lower dimensional Euclidean space.
Infinite forms can be extended to tessellate a hyperbolic space
. Hyperbolic space is like normal space at a small scale, but parallel lines diverge at a distance. This allows vertex figures to have negative angle defects
, like making a vertex with 7 equilateral triangles and allowing it to lie flat. It cannot be done in a regular plane, but can be at the right scale of a hyperbolic plane.
There are no nonconvex Euclidean tessellations in any number of dimensions.
s, or tilings, of spherical space. Tessellations of euclidean and hyperbolic space may also be considered regular polytopes. Note that an 'n'-dimensional polytope actually tessellates a space of one dimension less. For example, the (three dimensional) platonic solids tessellate the 'two'-dimensional 'surface' of the sphere.
, represented by the empty Schläfli symbol {}.
s. Regular polygons are equilateral
and cyclic. A p-gonal regular polygon is represented by Schläfli symbol {p}.
Usually only convex polygon
s are considered regular, but star polygons, like the pentagram
, can also be considered regular. They use the same vertices as the convex forms, but connect in an alternate connectivity which passes around the circle more than once to complete.
Star polygons should be called nonconvex rather than concave because the intersecting edges do not generate new vertices and all the vertices exist on a circle boundary.
.
{2} can be considered degenerate regular polygons. They can exist nondegenerately in non-Euclidean spaces like on the surface of a sphere
or torus
.
s of the convex regular polygons.
In general, for any natural number n, there are n-pointed non-convex regular polygonal stars with Schläfli symbols {n/m} for all m such that m < n/2 (strictly speaking {n/m}={n/(n−m)}) and m and n are coprime
.
. This has infinitely many vertices and edges. Its Schläfli symbol is {∞}, and Coxeter diagram .
...
...
:
A regular polyhedron with Schläfli symbol
has a regular face type 
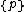, and regular vertex figure
.
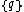A vertex figure
(of a polyhedron) is a polygon, seen by connecting those vertices which are one edge away from a given vertex. For regular polyhedra, this vertex figure is always a regular (and planar) polygon.
Existence of a regular polyhedron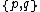
is constrained by an inequality, related to the vertex figure's angle defect
:
By enumerating the permutation
s, we find 5 convex forms, 4 nonconvex forms and 3 plane tilings, all with polygons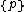
and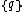 
limited to:
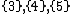, {5/2}, and 
.
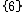Beyond Euclidean space, there is an infinite set of regular hyperbolic tilings.
are called the 5 Platonic solid
s. The vertex figure
is given with each vertex count. All these polyhedra have an Euler characteristic
(χ) of 2.
, the hosohedron {2,n} and dihedron
{n,2} can be considered regular polyhedra (tiling
s of the sphere
).
Some include:
are called the Kepler–Poinsot polyhedra and there are four of them, based on the vertex arrangement
s of the dodecahedron {5,3} and icosahedron
{3,5}:
As spherical tilings, these nonconvex forms overlap the sphere multiple times, called its density, being 3 or 7 for these forms. The tiling images show a single spherical polygon face in yellow.
(χ) of 0.
There is one degenerate regular tiling, {∞,2}, made from two apeirogon
s, each filling half the plane. This tiling is related to a 2-faced dihedron
, {p,2}, on the sphere.
(p, q, r) the same holds true for 1/p + 1/q + 1/r < 1.
There are 2 infinite forms of hyperbolic tilings whose faces
or vertex figure
s are star polygons: {m/2, m} and their duals {m,m/2} with m=7,9,11,...
There are a number of different ways to display the hyperbolic plane, including the Poincaré disc model which maps the plane into a circle, as shown below. It should be recognized that all of the polygon faces in the tilings below are equal-sized and only appear to get smaller near the edges due to the projection applied, very similar to the effect of a camera fisheye lens
.
A sampling:
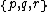have cells of type 
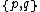, faces of type 
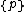, edge figures
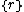, and vertex figures 
.
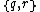The existence of a regular four-dimensional polytope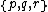
is constrained by the existence of the regular polyhedra 
.
Each will exist in a space dependent upon this expression:
These constraints allow for 21 forms: 6 are convex, 10 are nonconvex, one is a Euclidean 3-space honeycomb, and 4 are hyperbolic honeycombs.
The Euler characteristic
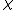for four-dimensional polytopes is
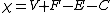
and is zero for all forms.
are shown in the table below. All these polychora have an Euler characteristic
(χ) of 0.
.
Regular ditopes (2 facets) include: {3,3,2}, {3,4,2}, {4,3,2}, {5,3,2}, {3,5,2}, {p,2,2}, and their hosotope duals (2 vertices): {2,3,3}, {2,4,3}, {2,3,4}, {2,3,5}, {2,5,3}.
Ludwig Schläfli
found four of them and skipped the last six because he would not allow forms that failed the Euler characteristic
on cells or vertex figures (Vertices-Edges+Faces-Cells = 0). Edmund Hess
(1843-1903) completed the full list of ten in his German book Einleitung in die Lehre von der Kugelteilung mit besonderer Berücksichtigung ihrer Anwendung auf die Theorie der Gleichflächigen und der gleicheckigen Polyeder (1883)http://www.hti.umich.edu/cgi/b/bib/bibperm?q1=ABN8623.0001.001.
There are 4 unique edge arrangements and 7 unique face arrangements from these 10 nonconvex four-dimensional polytopes, shown as orthogonal projections:
There are 4 failed potential nonconvex regular polychora permutations: {3,5/2,3}, {4,3,5/2}, {5/2,3,4}, {5/2,3,5/2}. Their cells and vertex figures exist, but they do not cover a hypersphere with a finite number of repetitions.
There is only one regular tessellation of 3-space (honeycombs
):
can be called hyperbolic honeycombs
. There are 4 regular honeycombs in H3:
Here are some projected images: The first shows the perspective from the center of the disc in a Beltrami–Klein model, and the second and third from the outside with a Poincaré ball model
.
There are also 11 H3 honeycombs which have infinite (Euclidean) cells and/or vertex figures: {3,3,6}, {6,3,3}, {3,4,4}, {4,4,3}, {3,6,3}, {4,3,6}, {6,3,4}, {4,4,4}, {5,3,6}, {6,3,5}, {6,3,6}.
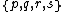where 
is the hypercell (or teron) type, 
is the cell type,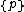 
is the face type, and 
is the face figure, 
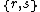is the edge figure, and 
is the vertex figure.
A 5-polytope has been called a polyteron, and if infinite (i.e. a honeycomb
).
A regular polytope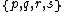
exists only if 
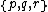and 
are regular polychora.
The space it fits in is based on the expression:
Enumeration of these constraints produce 3 convex polytopes, zero nonconvex polytopes, 3 4-space tessellations, and 5 hyperbolic 4-space tessellations. There are no non-convex regular polytopes in five dimensions or higher.
5 dimensions
6 dimensions
7 dimensions
8 dimensions
9 dimensions
10 dimensions
...
) that can tessellate four dimensional space:
The hypercube honeycomb is the only family of regular honeycombs that can tessellate each dimension, five or higher, formed by hypercube
facets, four around every ridge
.
and four kinds of star-honeycombs in H4 space.
Five convex regular honeycombs in H4:
There are four regular star-honeycombs in H4 space:
There are also 2 H4 honeycombs with infinite (Euclidean) facets or vertex figures: {3,4,3,4}, {4,3,4,3}
There are no finite-faceted regular tessellations of hyperbolic space of dimension 5 or higher.
There are 5 regular honeycombs in H5 with infinite (Euclidean) facets or vertex figures: {3,4,3,3,3}, {3,3,4,3,3}, {3,3,3,4,3}, {3,4,3,3,4}, {4,3,3,4,3}.
Even allowing for infinite (Euclidean) facets and/or vertex figures, there are no regular tessellations of hyperbolic space of dimension 6 or higher.
Some people regard apeirotopes as just a special kind of polytope, while others regard them as rather different things.
is a regular division of an infinitely long line into equal segments, joined by vertices. It has regular embeddings in the plane, and in higher-dimensional spaces. In two dimensions it can form a straight line or a zig-zag. In three dimensions, it traces out a helical spiral. The zig-zag and spiral forms are said to be skew.
is an infinite polyhedral surface. Like an apeirogon, it can be flat or skew. A flat apeirohedron is just a tiling of the plane. A skew apeirohedron is an intricate honeycomb-like structure which divides space into two regions.
There are thirty regular apeirohedra in Euclidean space. These include the tessellations of type
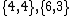and 
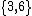above, as well as (in the plane) polytopes of type:
, 
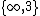and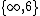 
, and in 3-dimensional space, blends of these with either an apeirogon or a line segment, and the "pure" 3-dimensional apeirohedra (12 in number)
See also regular skew polyhedron
.
s arose out of an attempt to study polytopes apart from the geometrical space they are embedded in. They include the tessellations of spherical, euclidean and hyperbolic space, tessellations of other manifold
s, and many other objects that do not have a well-defined topology, but instead may be characterised by their "local" topology. There are infinitely many in every dimension. See this atlas for a sample. Some notable examples of abstract polytopes that do not appear elsewhere in this list are the 11-cell
and the 57-cell.
Regular polytope
In mathematics, a regular polytope is a polytope whose symmetry is transitive on its flags, thus giving it the highest degree of symmetry. All its elements or j-faces — cells, faces and so on — are also transitive on the symmetries of the polytope, and are regular polytopes of...
s in Euclidean
Euclidean geometry
Euclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions from these...
, spherical
Spherical geometry
Spherical geometry is the geometry of the two-dimensional surface of a sphere. It is an example of a geometry which is not Euclidean. Two practical applications of the principles of spherical geometry are to navigation and astronomy....
and hyperbolic
Hyperbolic geometry
In mathematics, hyperbolic geometry is a non-Euclidean geometry, meaning that the parallel postulate of Euclidean geometry is replaced...
spaces.
The Schläfli symbol notation describes every regular polytope, and is used widely below as a compact reference name for each.
The regular polytopes are grouped by dimension and subgrouped by convex, nonconvex and infinite forms. Nonconvex forms use the same vertices as the convex forms, but have intersecting facets
Facet (mathematics)
A facet of a simplicial complex is a maximal simplex.In the general theory of polyhedra and polytopes, two conflicting meanings are currently jostling for acceptability:...
. Infinite forms tessellate
Tessellation
A tessellation or tiling of the plane is a pattern of plane figures that fills the plane with no overlaps and no gaps. One may also speak of tessellations of parts of the plane or of other surfaces. Generalizations to higher dimensions are also possible. Tessellations frequently appeared in the art...
a one lower dimensional Euclidean space.
Infinite forms can be extended to tessellate a hyperbolic space
Hyperbolic space
In mathematics, hyperbolic space is a type of non-Euclidean geometry. Whereas spherical geometry has a constant positive curvature, hyperbolic geometry has a negative curvature: every point in hyperbolic space is a saddle point...
. Hyperbolic space is like normal space at a small scale, but parallel lines diverge at a distance. This allows vertex figures to have negative angle defects
Defect (geometry)
In geometry, the defect means the failure of some angles to add up to the expected amount of 360° or 180°, when such angles in the plane would...
, like making a vertex with 7 equilateral triangles and allowing it to lie flat. It cannot be done in a regular plane, but can be at the right scale of a hyperbolic plane.
Overview
This table shows a summary of regular polytope counts by dimension.| Dimension | Convex | Nonconvex | Convex Euclidean tessellations |
Convex hyperbolic tessellations |
Nonconvex hyperbolic tessellations |
Abstract Polytopes |
|---|---|---|---|---|---|---|
| 1 | 1 line segment | 0 | 0 | 0 | 0 | 1 |
| 2 | ∞ polygons | ∞ star polygons | 1 | 1 | 0 | ∞ |
| 3 | 5 Platonic solids | 4 Kepler–Poinsot solids | 3 tilings | ∞ | ∞ | ∞ |
| 4 | 6 convex polychora | 10 Schläfli–Hess polychora | 1 honeycomb | 4 | 0 | ∞ |
| 5 | 3 convex 5-polytopes | 0 nonconvex 5-polytopes | 3 tessellations | 5 | 4 | ∞ |
| 6+ | 3 | 0 | 1 | 0 | 0 | ∞ |
There are no nonconvex Euclidean tessellations in any number of dimensions.
Tessellations
The classical convex polytopes may be considered tessellationTessellation
A tessellation or tiling of the plane is a pattern of plane figures that fills the plane with no overlaps and no gaps. One may also speak of tessellations of parts of the plane or of other surfaces. Generalizations to higher dimensions are also possible. Tessellations frequently appeared in the art...
s, or tilings, of spherical space. Tessellations of euclidean and hyperbolic space may also be considered regular polytopes. Note that an 'n'-dimensional polytope actually tessellates a space of one dimension less. For example, the (three dimensional) platonic solids tessellate the 'two'-dimensional 'surface' of the sphere.
One-dimensional regular polytope
There is only one polytope in 1 dimensions, whose boundaries are the two endpoints of a line segmentLine segment
In geometry, a line segment is a part of a line that is bounded by two end points, and contains every point on the line between its end points. Examples of line segments include the sides of a triangle or square. More generally, when the end points are both vertices of a polygon, the line segment...
, represented by the empty Schläfli symbol {}.
Two-dimensional regular polytopes
The two dimensional polytopes are called polygonPolygon
In geometry a polygon is a flat shape consisting of straight lines that are joined to form a closed chain orcircuit.A polygon is traditionally a plane figure that is bounded by a closed path, composed of a finite sequence of straight line segments...
s. Regular polygons are equilateral
Equilateral
In geometry, an equilateral polygon is a polygon which has all sides of the same length.For instance, an equilateral triangle is a triangle of equal edge lengths...
and cyclic. A p-gonal regular polygon is represented by Schläfli symbol {p}.
Usually only convex polygon
Convex polygon
In geometry, a polygon can be either convex or concave .- Convex polygons :A convex polygon is a simple polygon whose interior is a convex set...
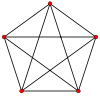
s are considered regular, but star polygons, like the pentagram
Pentagram
A pentagram is the shape of a five-pointed star drawn with five straight strokes...
, can also be considered regular. They use the same vertices as the convex forms, but connect in an alternate connectivity which passes around the circle more than once to complete.
Star polygons should be called nonconvex rather than concave because the intersecting edges do not generate new vertices and all the vertices exist on a circle boundary.
Convex
The Schläfli symbol {p} represents a regular p-gonRegular polygon
A regular polygon is a polygon that is equiangular and equilateral . Regular polygons may be convex or star.-General properties:...
.
| Name | Triangle (2-simplex Simplex In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,... ) |
Square Square (geometry) In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles... (2-orthoplex Cross-polytope In geometry, a cross-polytope, orthoplex, hyperoctahedron, or cocube is a regular, convex polytope that exists in any number of dimensions. The vertices of a cross-polytope are all the permutations of . The cross-polytope is the convex hull of its vertices... ) (2-cube Hypercube In geometry, a hypercube is an n-dimensional analogue of a square and a cube . It is a closed, compact, convex figure whose 1-skeleton consists of groups of opposite parallel line segments aligned in each of the space's dimensions, perpendicular to each other and of the same length.An... ) |
Pentagon Pentagon In geometry, a pentagon is any five-sided polygon. A pentagon may be simple or self-intersecting. The sum of the internal angles in a simple pentagon is 540°. A pentagram is an example of a self-intersecting pentagon.- Regular pentagons :In a regular pentagon, all sides are equal in length and... |
Hexagon | Heptagon | Octagon | |
|---|---|---|---|---|---|---|---|
| Schläfli | {3} | {4} | {5} | {6} | {7} | {8} | |
| Coxeter Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... |
|||||||
| Image |  |
 |
 |
 |
 |
 |
|
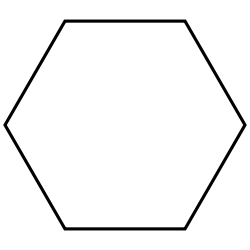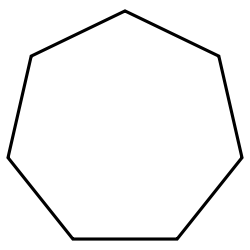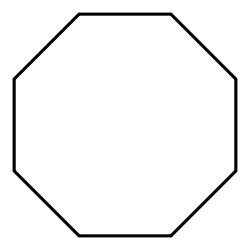| Name | Nonagon | Decagon Decagon In geometry, a decagon is any polygon with ten sides and ten angles, and usually refers to a regular decagon, having all sides of equal length and each internal angle equal to 144°... |
Hendecagon Hendecagon In geometry, a hendecagon is an 11-sided polygon.... |
Dodecagon Dodecagon In geometry, a dodecagon is any polygon with twelve sides and twelve angles.- Regular dodecagon :It usually refers to a regular dodecagon, having all sides of equal length and all angles equal to 150°... |
Triskaidecagon | Tetradecagon | |
| Schläfli | {9} | {10} | {11} | {12} | {13} | {14} | |
| Dynkin | |||||||
| Image |  |
 |
 |
 |
|||
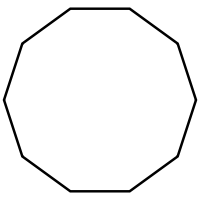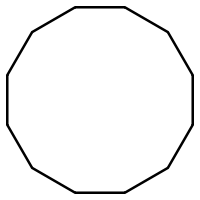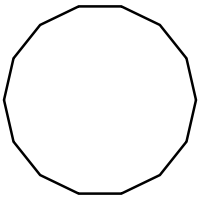| Name | Pentadecagon Pentadecagon In geometry, a pentadecagon is any 15-sided, 15-angled, polygon.- Regular pentadecagon:A regular pentadecagon has interior angles of 156°, and with a side length a, has an area given by... |
Hexadecagon Hexadecagon In mathematics, a hexadecagon is a polygon with 16 sides and 16 vertices.- Regular hexadecagon :A regular hexadecagon is constructible with a compass and straightedge.... |
Heptadecagon Heptadecagon In geometry, a heptadecagon is a seventeen-sided polygon.-Heptadecagon construction:The regular heptadecagon is a constructible polygon, as was shown by Carl Friedrich Gauss in 1796 at the age of 19.... |
Octadecagon Octadecagon An octadecagon is a polygon with 18 sides and 18 vertices. Another name for an octadecagon is octakaidecagon.- Construction :A regular octadecagon cannot be constructed using compass and straightedge.- Petrie polygons :... |
Enneadecagon Enneadecagon In geometry, an enneadecagon is a polygon with 19 sides and angles. It is also known as an enneakaidecagon or a nonadecagon.The radius of the circumcircle of the regular enneadecagon with side length t is... |
Icosagon Icosagon In geometry, an icosagon is a twenty-sided polygon. The sum of any icosagon's interior angles is 3240 degrees.One interior angle in a regular icosagon is 162° meaning that one exterior angle would be 18°... |
...p-gon Regular polygon A regular polygon is a polygon that is equiangular and equilateral . Regular polygons may be convex or star.-General properties:... |
| Schläfli | {15} | {16} | {17} | {18} | {19} | {20} | {p} |
| Dynkin | |||||||
| Image |  |
 |
 |
 |
 |
Degenerate (spherical)
The regular henagon {1} and regular digonDigon
In geometry, a digon is a polygon with two sides and two vertices. It is degenerate in a Euclidean space, but may be non-degenerate in a spherical space.A digon must be regular because its two edges are the same length...
{2} can be considered degenerate regular polygons. They can exist nondegenerately in non-Euclidean spaces like on the surface of a sphere
Sphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
or torus
Torus
In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
.
| Name | Henagon | Digon Digon In geometry, a digon is a polygon with two sides and two vertices. It is degenerate in a Euclidean space, but may be non-degenerate in a spherical space.A digon must be regular because its two edges are the same length... |
|---|---|---|
| Schläfli symbol | {1} | {2} |
| Coxeter diagram Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... |
||
| Image |  |
 |
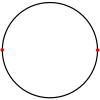Non-convex
There exist infinitely many non-convex regular polytopes in two dimensions, whose Schläfli symbols consist of rational numbers {n/m}. They are called star polygons and share the same vertex arrangementVertex arrangement
In geometry, a vertex arrangement is a set of points in space described by their relative positions. They can be described by their use in polytopes....
s of the convex regular polygons.
In general, for any natural number n, there are n-pointed non-convex regular polygonal stars with Schläfli symbols {n/m} for all m such that m < n/2 (strictly speaking {n/m}={n/(n−m)}) and m and n are coprime
Coprime
In number theory, a branch of mathematics, two integers a and b are said to be coprime or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor being 1...
.
| Name | Pentagram Pentagram A pentagram is the shape of a five-pointed star drawn with five straight strokes... |
Heptagram Heptagram A heptagram or septegram is a seven-pointed star drawn with seven straight strokes.- Geometry :In general, a heptagram is any self-intersecting heptagon .... s |
Octagram Octagram In geometry, an octagram is an eight-sided star polygon.- Geometry :In general, an octagram is any self-intersecting octagon .... |
Enneagrams Enneagram (geometry) In geometry, an enneagram is a nine-pointed geometric figure. It is sometimes called a nonagram.-Regular enneagram:A regular enneagram is constructed using the same points as the regular enneagon but connected in fixed steps... |
Decagram | ...n-agrams | ||
|---|---|---|---|---|---|---|---|---|
| Schläfli | {5/2} | {7/2} | {7/3} | {8/3} | {9/2} | {9/4} | {10/3} | {p/q} |
| Coxeter Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... |
||||||||
| Image |  |
 |
 |
 |
 |
 |
 |
|
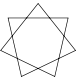Tessellation
There is one tessellation of the line, giving one polytope, the (two-dimensional) apeirogonApeirogon
An apeirogon is a degenerate polygon with a countably infinite number of sides. It is the limit of a sequence of polygons with more and more sides.Like any polygon, it is a sequence of line segments and angles...
. This has infinitely many vertices and edges. Its Schläfli symbol is {∞}, and Coxeter diagram .
...
...Three-dimensional regular polytopes
In three dimensions, polytopes are called polyhedraPolyhedron
In elementary geometry a polyhedron is a geometric solid in three dimensions with flat faces and straight edges...
:
A regular polyhedron with Schläfli symbol
has a regular face type 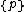, and regular vertex figureVertex figure
In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:...
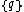.A vertex figure
Vertex figure
In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:...
(of a polyhedron) is a polygon, seen by connecting those vertices which are one edge away from a given vertex. For regular polyhedra, this vertex figure is always a regular (and planar) polygon.
Existence of a regular polyhedron
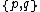is constrained by an inequality, related to the vertex figure's angle defectDefect (geometry)
In geometry, the defect means the failure of some angles to add up to the expected amount of 360° or 180°, when such angles in the plane would...
:
-
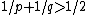: Polyhedron (existing in Euclidean 3-space) -
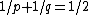: Euclidean plane tiling -
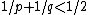: Hyperbolic plane tiling
By enumerating the permutation
Permutation
In mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
s, we find 5 convex forms, 4 nonconvex forms and 3 plane tilings, all with polygons
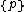and 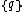limited to: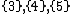, {5/2}, and 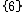.Beyond Euclidean space, there is an infinite set of regular hyperbolic tilings.
Convex
The convex regular polyhedraPolyhedron
In elementary geometry a polyhedron is a geometric solid in three dimensions with flat faces and straight edges...
are called the 5 Platonic solid
Platonic solid
In geometry, a Platonic solid is a convex polyhedron that is regular, in the sense of a regular polygon. Specifically, the faces of a Platonic solid are congruent regular polygons, with the same number of faces meeting at each vertex; thus, all its edges are congruent, as are its vertices and...
s. The vertex figure
Vertex figure
In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:...
is given with each vertex count. All these polyhedra have an Euler characteristic
Euler characteristic
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...
(χ) of 2.
| Name | Schläfli {p,q} |
Coxeter Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... |
Image (transparent) |
Image (solid) |
Image (sphere) |
Faces Face (geometry) In geometry, a face of a polyhedron is any of the polygons that make up its boundaries. For example, any of the squares that bound a cube is a face of the cube... {p} |
Edges Edge (geometry) In geometry, an edge is a one-dimensional line segment joining two adjacent zero-dimensional vertices in a polygon. Thus applied, an edge is a connector for a one-dimensional line segment and two zero-dimensional objects.... |
Vertices Vertex (geometry) In geometry, a vertex is a special kind of point that describes the corners or intersections of geometric shapes.-Of an angle:... {q} |
Symmetry Symmetry group The symmetry group of an object is the group of all isometries under which it is invariant with composition as the operation... |
Dual Dual polyhedron In geometry, polyhedra are associated into pairs called duals, where the vertices of one correspond to the faces of the other. The dual of the dual is the original polyhedron. The dual of a polyhedron with equivalent vertices is one with equivalent faces, and of one with equivalent edges is another... |
|---|---|---|---|---|---|---|---|---|---|---|
| Tetrahedron Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids... (3-simplex Simplex In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,... ) (Triangular pyramid) |
{3,3} |  |
 |
4 {3} |
6 | 4 {3} |
Td | (self) | ||
| Cube Cube In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and... (3-cube Hypercube In geometry, a hypercube is an n-dimensional analogue of a square and a cube . It is a closed, compact, convex figure whose 1-skeleton consists of groups of opposite parallel line segments aligned in each of the space's dimensions, perpendicular to each other and of the same length.An... ) (Hexahedron) |
{4,3} |  |
 |
 |
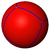6 {4} |
12 | 8 {3} |
Oh | Octahedron | |
| Octahedron Octahedron In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex.... (3-orthoplex Cross-polytope In geometry, a cross-polytope, orthoplex, hyperoctahedron, or cocube is a regular, convex polytope that exists in any number of dimensions. The vertices of a cross-polytope are all the permutations of . The cross-polytope is the convex hull of its vertices... ) |
{3,4} |  |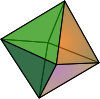
 |
 |
8 {3} |
12 | 6 {4} |
Oh | Cube | |
| Dodecahedron | {5,3} |  |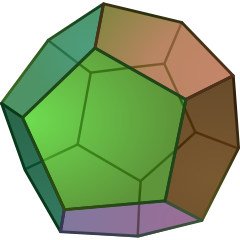
 |
 |
12 {5} |
30 | 20 {3}2 |
Ih | Icosahedron | |
| Icosahedron Icosahedron In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids.... |
{3,5} |  |
 |
 |
20 {3} |
30 | 12 {5} |
Ih | Dodecahedron |
Degenerate (spherical)
In spherical geometrySpherical geometry
Spherical geometry is the geometry of the two-dimensional surface of a sphere. It is an example of a geometry which is not Euclidean. Two practical applications of the principles of spherical geometry are to navigation and astronomy....
, the hosohedron {2,n} and dihedron
Dihedron
A dihedron is a type of polyhedron, made of two polygon faces which share the same set of edges. In three-dimensional Euclidean space, it is degenerate if its faces are flat, while in three-dimensional spherical space, a dihedron with flat faces can be thought of as a lens, an example of which is...
{n,2} can be considered regular polyhedra (tiling
Tessellation
A tessellation or tiling of the plane is a pattern of plane figures that fills the plane with no overlaps and no gaps. One may also speak of tessellations of parts of the plane or of other surfaces. Generalizations to higher dimensions are also possible. Tessellations frequently appeared in the art...
s of the sphere
Sphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
).
Some include:
| Name | Schläfli {p,q} |
Coxeter diagram Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... |
Image (sphere) |
Faces Face (geometry) In geometry, a face of a polyhedron is any of the polygons that make up its boundaries. For example, any of the squares that bound a cube is a face of the cube... {p} |
Edges Edge (geometry) In geometry, an edge is a one-dimensional line segment joining two adjacent zero-dimensional vertices in a polygon. Thus applied, an edge is a connector for a one-dimensional line segment and two zero-dimensional objects.... |
Vertices Vertex (geometry) In geometry, a vertex is a special kind of point that describes the corners or intersections of geometric shapes.-Of an angle:... {q} |
Symmetry | Dual Dual polyhedron In geometry, polyhedra are associated into pairs called duals, where the vertices of one correspond to the faces of the other. The dual of the dual is the original polyhedron. The dual of a polyhedron with equivalent vertices is one with equivalent faces, and of one with equivalent edges is another... |
|---|---|---|---|---|---|---|---|---|
| Hengonal dihedron | {1,2} |  |
2 {1} |
1 | 1 {2} |
C1v (*22) |
Hengonal hosohedron | |
| Hengonal hosohedron | {2,1} | 1 {2} |
1 | 2 {1} |
C1v (*22) |
Hengonal dihedron | ||
| Digonal dihedron Digonal hosohedron |
{2,2} |  |
2 {2} |
2 | 2 {2} |
D2h (*222) |
Self | |
| Trigonal hosohedron | {2,3} |  |
3 {2} |
3 | 2 {3} |
D3h (*322) |
Trigonal dihedron | |
| Trigonal dihedron | {3,2} |  |
2 {3} |
3 | 3 {2} |
D3h (*322) |
Trigonal hosohedron | |
| Hexagonal hosohedron | {2,6} |  |
6 {2} |
6 | 2 {6} |
D3h (*622) |
Hexagonal dihedron |
Non-convex
The regular star polyhedraStar polyhedron
In geometry, a star polyhedron is a polyhedron which has some repetitive quality of nonconvexity giving it a star-like visual quality.There are two general kinds of star polyhedron:*Polyhedra which self-intersect in a repetitive way....
are called the Kepler–Poinsot polyhedra and there are four of them, based on the vertex arrangement
Vertex arrangement
In geometry, a vertex arrangement is a set of points in space described by their relative positions. They can be described by their use in polytopes....
s of the dodecahedron {5,3} and icosahedron
Icosahedron
In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids....
{3,5}:
As spherical tilings, these nonconvex forms overlap the sphere multiple times, called its density, being 3 or 7 for these forms. The tiling images show a single spherical polygon face in yellow.
| Name | Image (transparent) |
Image (solid) |
Image (sphere) |
Stellation Stellation Stellation is a process of constructing new polygons , new polyhedra in three dimensions, or, in general, new polytopes in n dimensions. The process consists of extending elements such as edges or face planes, usually in a symmetrical way, until they meet each other again... diagram |
Schläfli {p,q} and Coxeter-Dynkin Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... |
Faces {p} |
Edges | Vertices {q} verf. Vertex figure In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:... |
χ Euler characteristic In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent... |
Density | Symmetry Symmetry group The symmetry group of an object is the group of all isometries under which it is invariant with composition as the operation... |
Dual Dual polyhedron In geometry, polyhedra are associated into pairs called duals, where the vertices of one correspond to the faces of the other. The dual of the dual is the original polyhedron. The dual of a polyhedron with equivalent vertices is one with equivalent faces, and of one with equivalent edges is another... |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
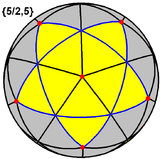
| Small stellated dodecahedron |  |
 |
 |
 |
{5/2,5} |
12 {5/2}  |
30 | 12 {5}  |
-6 | 3 | Ih | Great dodecahedron |
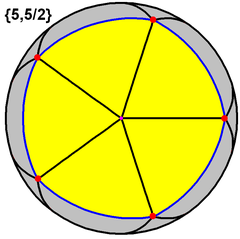
| Great dodecahedron |  |
 |
 |
 |
{5,5/2} |
12 {5} |
30 | 12 {5/2} |
-6 | 3 | Ih | Small stellated dodecahedron |
| Great stellated dodecahedron |  |
 |
 |
 |
{5/2,3} |
12 {5/2} |
30 | 20 {3}  |
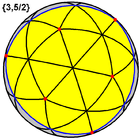
2 | 7 | Ih | Great icosahedron |
| Great icosahedron |  |
 |
 |
 |
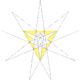{3,5/2} |
20 {3} |
30 | 12 {5/2} |
2 | 7 | Ih | Great stellated dodecahedron |
Euclidean tilings
There are three regular tessellations of the plane. All three have an Euler characteristicEuler characteristic
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...
(χ) of 0.
| Name | Schläfli {p,q} | Coxeter diagram Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... |
Image | Face type {p} |
Vertex figure Vertex figure In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:... {q} |
Symmetry Symmetry group The symmetry group of an object is the group of all isometries under which it is invariant with composition as the operation... |
Dual |
|---|---|---|---|---|---|---|---|
| Square tiling (Quadrille) |
{4,4} |  |
{4} | {4} | *442 (p4m) |
(self) | |
| Triangular tiling (Deltille) |
{3,6} |  |
{3} | {6} | *632 (p6m) |
Hexagonal tiling | |
| Hexagonal tiling (Hextille) |
{6,3} |  |
{6} | {3} | *632 (p6m) |
Triangular tiling |
There is one degenerate regular tiling, {∞,2}, made from two apeirogon
Apeirogon
An apeirogon is a degenerate polygon with a countably infinite number of sides. It is the limit of a sequence of polygons with more and more sides.Like any polygon, it is a sequence of line segments and angles...
s, each filling half the plane. This tiling is related to a 2-faced dihedron
Dihedron
A dihedron is a type of polyhedron, made of two polygon faces which share the same set of edges. In three-dimensional Euclidean space, it is degenerate if its faces are flat, while in three-dimensional spherical space, a dihedron with flat faces can be thought of as a lens, an example of which is...
, {p,2}, on the sphere.
Euclidean star-tilings
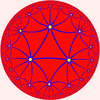
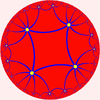
There are no regular plane tilings of star polygons. There are many enumerations that fit in the plane (1/p + 1/q = 1/2), like {8/3,8}, {10/3,5}, {5/2,10}, {12/5,12}, etc, but none repeat periodically.Hyperbolic tilings
Tessellations of hyperbolic 2-space can be called hyperbolic tilings. There are infinitely many regular tilings in H2. As stated above, every positive integer pair {p,q} such that 1/p + 1/q < 1/2 gives a hyperbolic tiling. In fact, for the general Schwarz triangleSchwarz triangle
In geometry, a Schwarz triangle, named after Hermann Schwarz is a spherical triangle that can be used to tile a sphere, possibly overlapping, through reflections in its edges. They were classified in ....
(p, q, r) the same holds true for 1/p + 1/q + 1/r < 1.
There are 2 infinite forms of hyperbolic tilings whose faces
Face (geometry)
In geometry, a face of a polyhedron is any of the polygons that make up its boundaries. For example, any of the squares that bound a cube is a face of the cube...
or vertex figure
Vertex figure
In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:...
s are star polygons: {m/2, m} and their duals {m,m/2} with m=7,9,11,...
There are a number of different ways to display the hyperbolic plane, including the Poincaré disc model which maps the plane into a circle, as shown below. It should be recognized that all of the polygon faces in the tilings below are equal-sized and only appear to get smaller near the edges due to the projection applied, very similar to the effect of a camera fisheye lens
Fisheye lens
In photography, a fisheye lens is a wide-angle lens that takes in a broad, panoramic and hemispherical image. Originally developed for use in meteorology to study cloud formation and called "whole-sky lenses", fisheye lenses quickly became popular in general photography for their unique, distorted...
.
A sampling:
| p \ q | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|
| 3 | (tetrahedron Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids... ) {3,3} |
(octahedron Octahedron In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex.... ) {3,4} |
(icosahedron Icosahedron In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids.... ) {3,5} |
 (deltille) {3,6} |
{3,7} |
{3,8} |
 {3,9} |
| 4 | (cube Cube In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and... ) {4,3} |
 (quadrille) {4,4} |
 {4,5} |
 {4,6} |
 {4,7} |
 {4,8} |
{4,9} |
| 5 | (dodecahedron) {5,3} |
 {5,4} |
 {5,5} |
 {5,6} |
{5,7} |
{5,8} |
{5,9} |
| 6 |  (hextille) {6,3} |
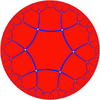 {6,4} |
{6,5} |
{6,6} |
{6,7} |
{6,8} |
{6,9} |
| 7 |  {7,3} |
 {7,4} |
{7,5} |
{7,6} |
{7,7} |
{7,8} |
{7,9} |
| 8 |  {8,3} |
{8,4} |
{8,5} |
{8,6} |
{8,7} |
{8,8} |
{8,9} |
| 9 |  {9,3} |
{9,4} |
{9,5} |
{9,6} |
{9,7} |
{9,8} |
{9,9} |
Four-dimensional regular polytopes
Regular 4-polytopes with Schläfli symbol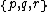 have cells of type 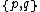, faces of type 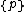, edge figures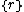, and vertex figures .
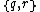- A vertex figureVertex figureIn geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:...
(of a four-dimensional polytope) is a polyhedron, seen by the arrangement of neighboring vertices around a given vertex. For regular four-dimensional polytopes, this vertex figure is a regular polyhedron. - An edge figure is a polygon, seen by the arrangement of faces around an edge. For regular four-dimensional polytopes, this edge figure will always be a regular polygon.
The existence of a regular four-dimensional polytope
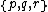is constrained by the existence of the regular polyhedra .Each will exist in a space dependent upon this expression:
-
-
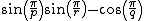
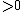: Hyperspherical 3-space honeycomb or 4-space tessellation -
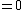: Euclidean 3-space honeycomb -
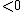: Hyperbolic 3-space honeycomb
-
These constraints allow for 21 forms: 6 are convex, 10 are nonconvex, one is a Euclidean 3-space honeycomb, and 4 are hyperbolic honeycombs.
The Euler characteristic
Euler characteristic
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...
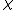for four-dimensional polytopes is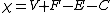and is zero for all forms.
Convex
The 6 convex polychoraConvex regular 4-polytope
In mathematics, a convex regular 4-polytope is a 4-dimensional polytope that is both regular and convex. These are the four-dimensional analogs of the Platonic solids and the regular polygons ....
are shown in the table below. All these polychora have an Euler characteristic
Euler characteristic
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...
(χ) of 0.
| Name |
Schläfli {p,q,r} |
Coxeter Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... |
Cells Cell (geometry) In geometry, a cell is a three-dimensional element that is part of a higher-dimensional object.- In polytopes :A cell is a three-dimensional polyhedron element that is part of the boundary of a higher-dimensional polytope, such as a polychoron or honeycomb For example, a cubic honeycomb is made... {p,q} |
Faces Face (geometry) In geometry, a face of a polyhedron is any of the polygons that make up its boundaries. For example, any of the squares that bound a cube is a face of the cube... {p} |
Edges Edge (geometry) In geometry, an edge is a one-dimensional line segment joining two adjacent zero-dimensional vertices in a polygon. Thus applied, an edge is a connector for a one-dimensional line segment and two zero-dimensional objects.... {r} |
Vertices Vertex (geometry) In geometry, a vertex is a special kind of point that describes the corners or intersections of geometric shapes.-Of an angle:... {q,r} |
Dual {r,q,p} |
|---|---|---|---|---|---|---|---|
| 5-cell (4-simplex Simplex In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,... ) (Pentachoron) |
{3,3,3} | 5 {3,3} |
10 {3} |
10 {3} |
5 {3,3} |
(self) | |
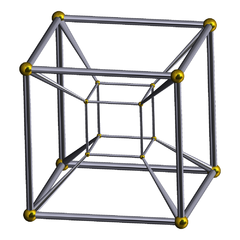
| 8-cell (4-cube Hypercube In geometry, a hypercube is an n-dimensional analogue of a square and a cube . It is a closed, compact, convex figure whose 1-skeleton consists of groups of opposite parallel line segments aligned in each of the space's dimensions, perpendicular to each other and of the same length.An... ) (Tesseract) |
{4,3,3} | 8 {4,3} |
24 {4} |
32 {3} |
16 {3,3} |
16-cell | |
| 16-cell 16-cell In four dimensional geometry, a 16-cell or hexadecachoron is a regular convex 4-polytope. It is one of the six regular convex 4-polytopes first described by the Swiss mathematician Ludwig Schläfli in the mid-19th century.... (4-orthoplex Cross-polytope In geometry, a cross-polytope, orthoplex, hyperoctahedron, or cocube is a regular, convex polytope that exists in any number of dimensions. The vertices of a cross-polytope are all the permutations of . The cross-polytope is the convex hull of its vertices... ) |
{3,3,4} | 16 {3,3} |
32 {3} |
24 {4} |
8 {3,4} |
Tesseract | |
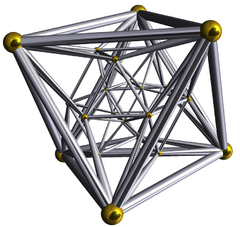
| 24-cell | {3,4,3} | 24 {3,4} |
96 {3} |
96 {3} |
24 {4,3} |
(self) | |
| 120-cell | {5,3,3} | 120 {5,3} |
720 {5} |
1200 {3} |
600 {3,3} |
600-cell | |
| 600-cell | {3,3,5} | 600 {3,3} |
1200 {3} |
720 {5} |
120 {3,5} |
120-cell |
| 5-cell | 8-cell | 16-cell 16-cell In four dimensional geometry, a 16-cell or hexadecachoron is a regular convex 4-polytope. It is one of the six regular convex 4-polytopes first described by the Swiss mathematician Ludwig Schläfli in the mid-19th century.... |
24-cell | 120-cell | 600-cell |
|---|---|---|---|---|---|
| {3,3,3} | {4,3,3} | {3,3,4} | {3,4,3} | {5,3,3} | {3,3,5} |
| Wireframe (Petrie polygon Petrie polygon In geometry, a Petrie polygon for a regular polytope of n dimensions is a skew polygon such that every consecutive sides belong to one of the facets... ) skew orthographic projection Orthographic projection Orthographic projection is a means of representing a three-dimensional object in two dimensions. It is a form of parallel projection, where all the projection lines are orthogonal to the projection plane, resulting in every plane of the scene appearing in affine transformation on the viewing surface... s |
|||||
 |
|||||
| Solid orthographic projection Orthographic projection Orthographic projection is a means of representing a three-dimensional object in two dimensions. It is a form of parallel projection, where all the projection lines are orthogonal to the projection plane, resulting in every plane of the scene appearing in affine transformation on the viewing surface... s |
|||||
| tetrahedral envelope Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids... (cell-centered) |
cubic envelope Cube In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and... (cell-centered) |
Cubic envelope Cube In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and... (cell-centered) |
 cuboctahedral envelope Cuboctahedron In geometry, a cuboctahedron is a polyhedron with eight triangular faces and six square faces. A cuboctahedron has 12 identical vertices, with two triangles and two squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such it is a quasiregular polyhedron,... (cell-centered) |
 truncated rhombic triacontahedron envelope Truncated rhombic triacontahedron The truncated rhombic triacontahedron is a convex polyhedron constructed as a truncation of the rhombic triacontahedron. It can more accurately be called a pentatruncated rhombic triacontahedron because only the order-5 vertices are truncated.... (cell-centered) |
Hexakis rectified truncated octahedron envelope (cell-centered) |
| Wireframe Schlegel diagrams (Perspective projection) | |||||
 (Cell-centered) |
 (Cell-centered) |
 (Cell-centered) |
 (Cell-centered) |
 (Cell-centered) |
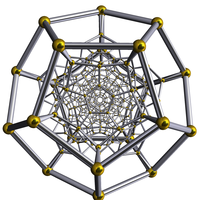(Cell-centered) |
| Wireframe stereographic projection Stereographic projection The stereographic projection, in geometry, is a particular mapping that projects a sphere onto a plane. The projection is defined on the entire sphere, except at one point — the projection point. Where it is defined, the mapping is smooth and bijective. It is conformal, meaning that it... s (Hyperspherical 3-sphere In mathematics, a 3-sphere is a higher-dimensional analogue of a sphere. It consists of the set of points equidistant from a fixed central point in 4-dimensional Euclidean space... ) |
|||||
 |
 |
 |
 |
 |
 |
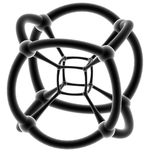Degenerate (spherical)
Ditopes and hosotopes exist as regular tessellations of the 3-sphere3-sphere
In mathematics, a 3-sphere is a higher-dimensional analogue of a sphere. It consists of the set of points equidistant from a fixed central point in 4-dimensional Euclidean space...
.
Regular ditopes (2 facets) include: {3,3,2}, {3,4,2}, {4,3,2}, {5,3,2}, {3,5,2}, {p,2,2}, and their hosotope duals (2 vertices): {2,3,3}, {2,4,3}, {2,3,4}, {2,3,5}, {2,5,3}.
Non-convex
There are ten regular four-dimensional star polytopes, which can be called Schläfli–Hess polytopes. Their vertices are based on the convex 120-cell {5,3,3} and 600-cell {3,3,5}.Ludwig Schläfli
Ludwig Schläfli
Ludwig Schläfli was a Swiss geometer and complex analyst who was one of the key figures in developing the notion of higher dimensional spaces. The concept of multidimensionality has since come to play a pivotal role in physics, and is a common element in science fiction...
found four of them and skipped the last six because he would not allow forms that failed the Euler characteristic
Euler characteristic
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...
on cells or vertex figures (Vertices-Edges+Faces-Cells = 0). Edmund Hess
Edmund Hess
Edmund Hess was a German mathematician who discovered several regular polytopes.- References :* Regular Polytopes, , Dover edition, ISBN 0-486-61480-8...
(1843-1903) completed the full list of ten in his German book Einleitung in die Lehre von der Kugelteilung mit besonderer Berücksichtigung ihrer Anwendung auf die Theorie der Gleichflächigen und der gleicheckigen Polyeder (1883)http://www.hti.umich.edu/cgi/b/bib/bibperm?q1=ABN8623.0001.001.
There are 4 unique edge arrangements and 7 unique face arrangements from these 10 nonconvex four-dimensional polytopes, shown as orthogonal projections:
| Name |
Wireframe | Solid | Schläfli {p, q,r} Coxeter–Dynkin |
Cells {p, q} |
Faces {p} |
Edges {r} |
Vertices {q, r} |
Density Polytope density In geometry, polytope density represents the number of windings of a polytope, particularly a uniform or regular polytope, around its center. It can be visually determined by counting the minimum number of facet crossings of a ray from the center to infinity... |
χ Euler characteristic In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent... |
Symmetry group Coxeter group In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example... |
Dual {r, q,p} |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Icosahedral 120-cell |  |
 |
{3,5,5/2} |
120 {3,5} Icosahedron In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids.... |
1200 {3} Triangle A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted .... |
720 {5/2} Pentagram A pentagram is the shape of a five-pointed star drawn with five straight strokes... |
120 {5,5/2} |
4 | 480 | H4 | Small stellated 120-cell |
| Small stellated 120-cell |  |
 |
{5/2,5,3} |
120 {5/2,5} |
720 {5/2} Pentagram A pentagram is the shape of a five-pointed star drawn with five straight strokes... |
1200 {3} Triangle A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted .... |
120 {5,3} |
4 | −480 | H4 | Icosahedral 120-cell |
| Great 120-cell | |
 |
{5,5/2,5} |
120 {5,5/2} |
720 {5} Pentagon In geometry, a pentagon is any five-sided polygon. A pentagon may be simple or self-intersecting. The sum of the internal angles in a simple pentagon is 540°. A pentagram is an example of a self-intersecting pentagon.- Regular pentagons :In a regular pentagon, all sides are equal in length and... |
720 {5} Pentagon In geometry, a pentagon is any five-sided polygon. A pentagon may be simple or self-intersecting. The sum of the internal angles in a simple pentagon is 540°. A pentagram is an example of a self-intersecting pentagon.- Regular pentagons :In a regular pentagon, all sides are equal in length and... |
120 {5/2,5} |
6 | 0 | H4 | Self-dual |
| Grand 120-cell | |
 |
{5,3,5/2} |
120 {5,3} |
720 {5} Pentagon In geometry, a pentagon is any five-sided polygon. A pentagon may be simple or self-intersecting. The sum of the internal angles in a simple pentagon is 540°. A pentagram is an example of a self-intersecting pentagon.- Regular pentagons :In a regular pentagon, all sides are equal in length and... |
720 {5/2} Pentagram A pentagram is the shape of a five-pointed star drawn with five straight strokes... |
120 {3,5/2} |
20 | 0 | H4 | Great stellated 120-cell |
| Great stellated 120-cell |  |
 |
{5/2,3,5} |
120 {5/2,3} |
720 {5/2} Pentagram A pentagram is the shape of a five-pointed star drawn with five straight strokes... |
720 {5} Pentagon In geometry, a pentagon is any five-sided polygon. A pentagon may be simple or self-intersecting. The sum of the internal angles in a simple pentagon is 540°. A pentagram is an example of a self-intersecting pentagon.- Regular pentagons :In a regular pentagon, all sides are equal in length and... |
120 {3,5} Icosahedron In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids.... |
20 | 0 | H4 | Grand 120-cell |
| Grand stellated 120-cell | |
 |
{5/2,5,5/2} |
120 {5/2,5} |
720 {5/2} Pentagram A pentagram is the shape of a five-pointed star drawn with five straight strokes... |
720 {5/2} Pentagram A pentagram is the shape of a five-pointed star drawn with five straight strokes... |
120 {5,5/2} |
66 | 0 | H4 | Self-dual |
| Great grand 120-cell | |
 |
{5,5/2,3} |
120 {5,5/2} |
720 {5} Pentagon In geometry, a pentagon is any five-sided polygon. A pentagon may be simple or self-intersecting. The sum of the internal angles in a simple pentagon is 540°. A pentagram is an example of a self-intersecting pentagon.- Regular pentagons :In a regular pentagon, all sides are equal in length and... |
1200 {3} Triangle A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted .... |
120 {5/2,3} |
76 | −480 | H4 | Great icosahedral 120-cell |
| Great icosahedral 120-cell | |
 |
{3,5/2,5} |
120 {3,5/2} |
1200 {3} Triangle A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted .... |
720 {5} Pentagon In geometry, a pentagon is any five-sided polygon. A pentagon may be simple or self-intersecting. The sum of the internal angles in a simple pentagon is 540°. A pentagram is an example of a self-intersecting pentagon.- Regular pentagons :In a regular pentagon, all sides are equal in length and... |
120 {5/2,5} |
76 | 480 | H4 | Great grand 120-cell |
| Grand 600-cell | |
 |
{3,3,5/2} |
600 {3,3} Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids... |
1200 {3} Triangle A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted .... |
720 {5/2} Pentagram A pentagram is the shape of a five-pointed star drawn with five straight strokes... |
120 {3,5/2} |
191 | 0 | H4 | Great grand stellated 120-cell |
| Great grand stellated 120-cell |  |
 |
{5/2,3,3} |
120 {5/2,3} |
720 {5/2} Pentagram A pentagram is the shape of a five-pointed star drawn with five straight strokes... |
1200 {3} Triangle A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted .... |
600 {3,3} Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids... |
191 | 0 | H4 | Grand 600-cell |
There are 4 failed potential nonconvex regular polychora permutations: {3,5/2,3}, {4,3,5/2}, {5/2,3,4}, {5/2,3,5/2}. Their cells and vertex figures exist, but they do not cover a hypersphere with a finite number of repetitions.
Tessellations of Euclidean 3-space
Honeycomb (geometry)
In geometry, a honeycomb is a space filling or close packing of polyhedral or higher-dimensional cells, so that there are no gaps. It is an example of the more general mathematical tiling or tessellation in any number of dimensions....
):
| Name | Schläfli symbol {p,q,r} |
Coxeter Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... |
Cell type {p,q} |
Face type {p} |
Edge figure {r} |
Vertex figure Vertex figure In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:... {q,r} |
χ Euler characteristic In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent... |
Dual |
|---|---|---|---|---|---|---|---|---|
| Cubic honeycomb Cubic honeycomb The cubic honeycomb is the only regular space-filling tessellation in Euclidean 3-space, made up of cubic cells. It has 4 cubes around every edge, and 8 cubes around each vertex. Its vertex figure is a regular octahedron.... |
{4,3,4} | {4,3} | {4} | {4} | {3,4} | 0 | Self-dual |
Tessellations of hyperbolic 3-space
Tessellations of hyperbolic 3-spaceHyperbolic space
In mathematics, hyperbolic space is a type of non-Euclidean geometry. Whereas spherical geometry has a constant positive curvature, hyperbolic geometry has a negative curvature: every point in hyperbolic space is a saddle point...
can be called hyperbolic honeycombs
Honeycomb (geometry)
In geometry, a honeycomb is a space filling or close packing of polyhedral or higher-dimensional cells, so that there are no gaps. It is an example of the more general mathematical tiling or tessellation in any number of dimensions....
. There are 4 regular honeycombs in H3:
| Name | Schläfli Symbol {p,q,r} |
Coxeter Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... |
Cell type {p,q} |
Face type {p} |
Edge figure {r} |
Vertex figure Vertex figure In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:... {q,r} |
χ Euler characteristic In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent... |
Dual |
|---|---|---|---|---|---|---|---|---|
| Icosahedral honeycomb | {3,5,3} | {3,5} | {3} | {3} | {5,3} | 0 | Self-dual | |
| Order-5 cubic honeycomb | {4,3,5} | {4,3} | {4} | {5} | {3,5} | 0 | {5,3,4} | |
| Order-4 dodecahedral honeycomb | {5,3,4} | {5,3} | {5} | {4} | {3,4} | 0 | {4,3,5} | |
| Order-5 dodecahedral honeycomb | {5,3,5} | {5,3} | {5} | {5} | {3,5} | 0 | Self-dual |
Here are some projected images: The first shows the perspective from the center of the disc in a Beltrami–Klein model, and the second and third from the outside with a Poincaré ball model
Poincaré disk model
In geometry, the Poincaré disk model, also called the conformal disk model, is a model of n-dimensional hyperbolic geometry in which the points of the geometry are in an n-dimensional disk, or unit ball, and the straight lines of the hyperbolic geometry are segments of circles contained in the disk...
.
 {5,3,4} (8 dodecahedra at a vertex) |
 {4,3,5} (20 cubes at a vertex) |
 {3,5,3} (12 icosahedra at a vertex) |
There are also 11 H3 honeycombs which have infinite (Euclidean) cells and/or vertex figures: {3,3,6}, {6,3,3}, {3,4,4}, {4,4,3}, {3,6,3}, {4,3,6}, {6,3,4}, {4,4,4}, {5,3,6}, {6,3,5}, {6,3,6}.
Five-dimensional regular polytopes and higher
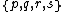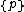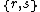In five dimensions, a regular polytope can be named as where is the hypercell (or teron) type, is the cell type, is the face type, and is the face figure, is the edge figure, and is the vertex figure.A 5-polytope has been called a polyteron, and if infinite (i.e. a honeycomb
Honeycomb (geometry)
In geometry, a honeycomb is a space filling or close packing of polyhedral or higher-dimensional cells, so that there are no gaps. It is an example of the more general mathematical tiling or tessellation in any number of dimensions....
).
- A vertex figureVertex figureIn geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:...
(of a 5-polytope) is a polychoron, seen by the arrangement of neighboring vertices to each vertex. - An edge figure (of a 5-polytope) is a polyhedron, seen by the arrangement of faces around each edge.
- A face figure (of a 5-polytope) is a polygon, seen by the arrangement of cells around each face.
A regular polytope
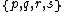exists only if 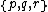and are regular polychora.The space it fits in is based on the expression:
-
-
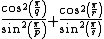
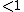: Spherical 4-space tessellation or 5-space polytope -
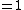: Euclidean 4-space tessellation -
: hyperbolic 4-space tessellation
-
Enumeration of these constraints produce 3 convex polytopes, zero nonconvex polytopes, 3 4-space tessellations, and 5 hyperbolic 4-space tessellations. There are no non-convex regular polytopes in five dimensions or higher.
Convex
In dimensions 5 and higher, there are only three kinds of convex regular polytopes.| Name | Schläfli Symbol {p1,...,pn−1} |
Coxeter Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... |
k-faces | Facet type |
Vertex figure Vertex figure In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:... |
Dual |
|---|---|---|---|---|---|---|
| n-simplex Simplex In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,... |
{3n−1} | ... | 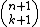 Binomial coefficient In mathematics, binomial coefficients are a family of positive integers that occur as coefficients in the binomial theorem. They are indexed by two nonnegative integers; the binomial coefficient indexed by n and k is usually written \tbinom nk , and it is the coefficient of the x k term in... |
{3n−2} | {3n−2} | Self-dual |
| n-cube Hypercube In geometry, a hypercube is an n-dimensional analogue of a square and a cube . It is a closed, compact, convex figure whose 1-skeleton consists of groups of opposite parallel line segments aligned in each of the space's dimensions, perpendicular to each other and of the same length.An... |
{4,3n−2} | ... |  |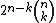
{4,3n−3} | {3n−2} | n-orthoplex |
| n-orthoplex Cross-polytope In geometry, a cross-polytope, orthoplex, hyperoctahedron, or cocube is a regular, convex polytope that exists in any number of dimensions. The vertices of a cross-polytope are all the permutations of . The cross-polytope is the convex hull of its vertices... |
{3n−2,4} | ... |  |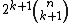
{3n−2} | {3n−3,4} | n-cube |
5 dimensions
| Name | Schläfli Symbol {p,q,r,s} Coxeter Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... |
Facets {p,q,r} |
Cells {p,q} |
Faces {p} |
Edges | Vertices | Face figure {s} |
Edge figure {r,s} |
Vertex figure Vertex figure In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:... {q,r,s} |
|---|---|---|---|---|---|---|---|---|---|
| 5-simplex Simplex In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,... |
{3,3,3,3} |
6 {3,3,3} |
15 {3,3} |
20 {3} |
15 | 6 | {3} | {3,3} | {3,3,3} |
| 5-cube Hypercube In geometry, a hypercube is an n-dimensional analogue of a square and a cube . It is a closed, compact, convex figure whose 1-skeleton consists of groups of opposite parallel line segments aligned in each of the space's dimensions, perpendicular to each other and of the same length.An... |
{4,3,3,3} |
10 {4,3,3} |
40 {4,3} |
80 {4} |
80 | 32 | {3} | {3,3} | {3,3,3} |
| 5-orthoplex Cross-polytope In geometry, a cross-polytope, orthoplex, hyperoctahedron, or cocube is a regular, convex polytope that exists in any number of dimensions. The vertices of a cross-polytope are all the permutations of . The cross-polytope is the convex hull of its vertices... |
{3,3,3,4} |
32 {3,3,3} |
80 {3,3} |
80 {3} |
40 | 10 | {4} | {3,4} | {3,3,4} |
5-simplex |
5-cube |
5-orthoplex |
6 dimensions
| Name | Schläfli symbol | Vertices | Edges | Faces | Cells | 4-faces | 5-faces!!χ | |
|---|---|---|---|---|---|---|---|---|
| 6-simplex | {3,3,3,3,3} | 7 | 21 | 35 | 35 | 21 | 7 | 0 |
| 6-cube | {4,3,3,3,3} | 64 | 192 | 240 | 160 | 60 | 12 | 0 |
| 6-orthoplex | {3,3,3,3,4} | 12 | 60 | 160 | 240 | 192 | 64 | 0 |
6-simplex |
6-cube |
6-orthoplex |
7 dimensions
| Name | Schläfli symbol | Vertices | Edges | Faces | Cells | 4-faces | 5-faces!!6-faces!!χ | ||
|---|---|---|---|---|---|---|---|---|---|
| 7-simplex | {3,3,3,3,3,3} | 8 | 28 | 56 | 70 | 56 | 28 | 8 | 2 |
| 7-cube | {4,3,3,3,3,3} | 128 | 448 | 672 | 560 | 280 | 84 | 14 | 2 |
| 7-orthoplex | {3,3,3,3,3,4} | 14 | 84 | 280 | 560 | 672 | 448 | 128 | 2 |
7-simplex |
7-cube |
7-orthoplex |
8 dimensions
| Name | Schläfli symbol | Vertices | Edges | Faces | Cells | 4-faces | 5-faces!!6-faces!!7-faces!!χ | |||
|---|---|---|---|---|---|---|---|---|---|---|
| 8-simplex | {3,3,3,3,3,3,3} | 9 | 36 | 84 | 126 | 126 | 84 | 36 | 9 | 0 |
| 8-cube | {4,3,3,3,3,3,3} | 256 | 1024 | 1792 | 1792 | 1120 | 448 | 112 | 16 | 0 |
| 8-orthoplex | {3,3,3,3,3,3,4} | 16 | 112 | 448 | 1120 | 1792 | 1792 | 1024 | 256 | 0 |
8-simplex |
8-cube |
8-orthoplex |
9 dimensions
| Name | Schläfli symbol | Vertices | Edges | Faces | Cells | 4-faces | 5-faces!!6-faces!!7-faces!!8-faces!!χ | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 9-simplex | {38} | 10 | 45 | 120 | 210 | 252 | 210 | 120 | 45 | 10 | 2 |
| 9-cube | {4,37} | 512 | 2304 | 4608 | 5376 | 4032 | 2016 | 672 | 144 | 18 | 2 |
| 9-orthoplex | {37,4} | 18 | 144 | 672 | 2016 | 4032 | 5376 | 4608 | 2304 | 512 | 2 |
9-simplex |
9-cube |
9-orthoplex |
10 dimensions
| Name | Schläfli symbol | Vertices | Edges | Faces | Cells | 4-faces | 5-faces!!6-faces!!7-faces!!8-faces!!9-faces!!χ | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 10-simplex 10-simplex In geometry, a 10-simplex is a self-dual regular 10-polytope. It has 11 vertices, 55 edges, 165 triangle faces, 330 tetrahedral cells, 462 5-cell 4-faces, 462 5-simplex 5-faces, 330 6-simplex 6-faces, 165 7-simplex 7-faces, 55 8-simplex 8-faces, and 11 9-simplex 9-faces... |
{39} | 11 | 55 | 165 | 330 | 462 | 462 | 330 | 165 | 55 | 11 | 0 |
| 10-cube 10-cube In geometry, a 10-cube is a ten-dimensional hypercube. It has 1024 vertices, 5120 edges, 11520 square faces, 15360 cubic cells, 13440 tesseract 4-faces, 8064 5-cube 5-faces, 3360 6-cube 6-faces, 960 7-cube 7-faces, 180 8-cube 8-faces, and 20 9-cube 9-faces.... |
{4,38} | 1024 | 5120 | 11520 | 15360 | 13440 | 8064 | 3360 | 960 | 180 | 20 | 0 |
| 10-orthoplex | {38,4} | 20 | 180 | 960 | 3360 | 8064 | 13440 | 15360 | 11520 | 5120 | 1024 | 0 |
10-simplex 10-simplex In geometry, a 10-simplex is a self-dual regular 10-polytope. It has 11 vertices, 55 edges, 165 triangle faces, 330 tetrahedral cells, 462 5-cell 4-faces, 462 5-simplex 5-faces, 330 6-simplex 6-faces, 165 7-simplex 7-faces, 55 8-simplex 8-faces, and 11 9-simplex 9-faces... |
10-cube 10-cube In geometry, a 10-cube is a ten-dimensional hypercube. It has 1024 vertices, 5120 edges, 11520 square faces, 15360 cubic cells, 13440 tesseract 4-faces, 8064 5-cube 5-faces, 3360 6-cube 6-faces, 960 7-cube 7-faces, 180 8-cube 8-faces, and 20 9-cube 9-faces.... |
10-orthoplex |
...
Tessellations of Euclidean 4-space
There are three kinds of infinite regular tessellations (honeycombsHoneycomb (geometry)
In geometry, a honeycomb is a space filling or close packing of polyhedral or higher-dimensional cells, so that there are no gaps. It is an example of the more general mathematical tiling or tessellation in any number of dimensions....
) that can tessellate four dimensional space:
| Name | Schläfli Symbol {p,q,r,s} |
Facet type {p,q,r} |
Cell type {p,q} |
Face type {p} |
Face figure {s} |
Edge figure {r,s} |
Vertex figure Vertex figure In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:... {q,r,s} |
Dual |
|---|---|---|---|---|---|---|---|---|
| Tesseractic honeycomb | {4,3,3,4} | {4,3,3} | {4,3} | {4} | {4} | {3,4} | {3,3,4} | Self-dual |
| Hexadecachoric honeycomb | {3,3,4,3} | {3,3,4} | {3,3} | {3} | {3} | {4,3} | {3,4,3} | {3,4,3,3} |
| Icositetrachoric honeycomb | {3,4,3,3} | {3,4,3} | {3,4} | {3} | {3} | {3,3} | {4,3,3} | {3,3,4,3} |
Projected portion of {4,3,3,4} (Tesseractic honeycomb) |
Projected portion of {3,3,4,3} (Hexadecachoronic honeycomb) |
 Projected portion of {3,4,3,3} (Icositetrachoronic honeycomb) |
The hypercube honeycomb is the only family of regular honeycombs that can tessellate each dimension, five or higher, formed by hypercube
Hypercube
In geometry, a hypercube is an n-dimensional analogue of a square and a cube . It is a closed, compact, convex figure whose 1-skeleton consists of groups of opposite parallel line segments aligned in each of the space's dimensions, perpendicular to each other and of the same length.An...
facets, four around every ridge
Ridge (geometry)
In geometry, a ridge is an -dimensional element of an n-dimensional polytope. It is also sometimes called a subfacet for having one lower dimension than a facet.By dimension, this corresponds to:*a vertex of a polygon;...
.
| Name | Schläfli {p1, p2, ..., pn−1} |
Facet type |
Vertex figure Vertex figure In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:... |
Dual |
|---|---|---|---|---|
| Square tiling | {4,4} | {4} | {4} | Self-dual |
| Cubic honeycomb Cubic honeycomb The cubic honeycomb is the only regular space-filling tessellation in Euclidean 3-space, made up of cubic cells. It has 4 cubes around every edge, and 8 cubes around each vertex. Its vertex figure is a regular octahedron.... |
{4,3,4} | {4,3} | {3,4} | Self-dual |
| Tesseractic honeycomb | {4,32,4} | {4,32} | {32,4} | Self-dual |
| Penteractic honeycomb | {4,33,4} | {4,33} | {33,4} | Self-dual |
| Hexeractic honeycomb | {4,34,4} | {4,34} | {34,4} | Self-dual |
| Hepteractic honeycomb | {4,35,4} | {4,35} | {35,4} | Self-dual |
| Octeractic honeycomb | {4,36,4} | {4,36} | {36,4} | Self-dual |
| n-hypercube honeycomb | {4,3n−2,4} | {4,3n−2} | {3n−2,4} | Self-dual |
Tessellations of hyperbolic 4-space
There are five kinds of convex regular honeycombsHoneycomb (geometry)
In geometry, a honeycomb is a space filling or close packing of polyhedral or higher-dimensional cells, so that there are no gaps. It is an example of the more general mathematical tiling or tessellation in any number of dimensions....
and four kinds of star-honeycombs in H4 space.
Five convex regular honeycombs in H4:
| Name | Schläfli Symbol {p,q,r,s} |
Facet type {p,q,r} |
Cell type {p,q} |
Face type {p} |
Face figure {s} |
Edge figure {r,s} |
Vertex figure Vertex figure In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:... {q,r,s} |
Dual |
|---|---|---|---|---|---|---|---|---|
| Order-5 5-cell honeycomb | {3,3,3,5} | {3,3,3} | {3,3} | {3} | {5} | {3,5} | {3,3,5} | {5,3,3,3} |
| Order-3 120-cell honeycomb | {5,3,3,3} | {5,3,3} | {5,3} | {5} | {3} | {3,3} | {3,3,3} | {3,3,3,5} |
| Order-5 tesseractic honeycomb | {4,3,3,5} | {4,3,3} | {4,3} | {4} | {5} | {3,5} | {3,3,5} | {5,3,3,4} |
| Order-4 120-cell honeycomb | {5,3,3,4} | {5,3,3} | {5,3} | {5} | {4} | {3,4} | {3,3,4} | {4,3,3,5} |
| Order-5 600-cell honeycomb | {5,3,3,5} | {5,3,3} | {5,3} | {5} | {5} | {3,5} | {3,3,5} | Self-dual |
There are four regular star-honeycombs in H4 space:
| Name | Schläfli Symbol {p,q,r,s} |
Facet type {p,q,r} |
Cell type {p,q} |
Face type {p} |
Face figure {s} |
Edge figure {r,s} |
Vertex figure Vertex figure In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:... {q,r,s} |
Dual |
|---|---|---|---|---|---|---|---|---|
| Order-3 small stellated 120-cell honeycomb | {5/2,5,3,3} | {5/2,5,3} | {5/2,5} | {5} | {5} | {3,3} | {5,3,3} | {3,3,5,5/2} |
| Pentagrammic-order 600-cell honeycomb | {3,3,5,5/2} | {3,3,5} | {3,3} | {3} | {5/2} | {5,5/2} | {3,5,5/2} | {5/2,5,3,3} |
| Order-5 icosahedral 120-cell honeycomb | {3,5,5/2,5} | {3,5,5/2} | {3,5} | {3} | {5} | {5/2,5} | {5,5/2,5} | {5,5/2,5,3} |
| Order-3 great 120-cell honeycomb | {5,5/2,5,3} | {5,5/2,5} | {5,5/2} | {5} | {3} | {5,3} | {5/2,5,3} | {3,5,5/2,5} |
There are also 2 H4 honeycombs with infinite (Euclidean) facets or vertex figures: {3,4,3,4}, {4,3,4,3}
There are no finite-faceted regular tessellations of hyperbolic space of dimension 5 or higher.
There are 5 regular honeycombs in H5 with infinite (Euclidean) facets or vertex figures: {3,4,3,3,3}, {3,3,4,3,3}, {3,3,3,4,3}, {3,4,3,3,4}, {4,3,3,4,3}.
Even allowing for infinite (Euclidean) facets and/or vertex figures, there are no regular tessellations of hyperbolic space of dimension 6 or higher.
Apeirotopes
An apeirotope is, like any other polytope, an unbounded hyper-surface. The difference is that whereas a polytope's hyper-surface curls back on itself to close round a finite volume of hyperspace, an apeirotope does not curl back.Some people regard apeirotopes as just a special kind of polytope, while others regard them as rather different things.
Two dimensions
A regular apeirogonApeirogon
An apeirogon is a degenerate polygon with a countably infinite number of sides. It is the limit of a sequence of polygons with more and more sides.Like any polygon, it is a sequence of line segments and angles...
is a regular division of an infinitely long line into equal segments, joined by vertices. It has regular embeddings in the plane, and in higher-dimensional spaces. In two dimensions it can form a straight line or a zig-zag. In three dimensions, it traces out a helical spiral. The zig-zag and spiral forms are said to be skew.
Three dimensions
An apeirohedronApeirohedron
An apeirohedron is a polyhedron having infinitely many faces. Like an ordinary polyhedron it forms a surface with no border. But where an ordinary polyhedral surface has no border because it folds round to close back on itself, an apeirohedron has no border because its surface is unbounded.Two main...
is an infinite polyhedral surface. Like an apeirogon, it can be flat or skew. A flat apeirohedron is just a tiling of the plane. A skew apeirohedron is an intricate honeycomb-like structure which divides space into two regions.
There are thirty regular apeirohedra in Euclidean space. These include the tessellations of type
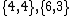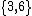and above, as well as (in the plane) polytopes of type: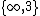, and 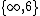, and in 3-dimensional space, blends of these with either an apeirogon or a line segment, and the "pure" 3-dimensional apeirohedra (12 in number)See also regular skew polyhedron
Regular skew polyhedron
In geometry, the regular skew polyhedra are generalizations to the set of regular polyhedron which include the possibility of nonplanar faces or vertex figures....
.
Abstract polytopes
The abstract polytopeAbstract polytope
In mathematics, an abstract polytope, informally speaking, is a structure which considers only the combinatorial properties of a traditional polytope, ignoring many of its other properties, such as angles, edge lengths, etc...
s arose out of an attempt to study polytopes apart from the geometrical space they are embedded in. They include the tessellations of spherical, euclidean and hyperbolic space, tessellations of other manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
s, and many other objects that do not have a well-defined topology, but instead may be characterised by their "local" topology. There are infinitely many in every dimension. See this atlas for a sample. Some notable examples of abstract polytopes that do not appear elsewhere in this list are the 11-cell
11-cell
In mathematics, the 11-cell is a self-dual abstract regular 4-polytope . Its 11 cells are hemi-icosahedral. It has 11 vertices, 55 edges and 55 faces. Its symmetry group is the projective special linear group L2, so it has660 symmetries...
and the 57-cell.
See also
- PolygonPolygonIn geometry a polygon is a flat shape consisting of straight lines that are joined to form a closed chain orcircuit.A polygon is traditionally a plane figure that is bounded by a closed path, composed of a finite sequence of straight line segments...
- Regular polygonRegular polygonA regular polygon is a polygon that is equiangular and equilateral . Regular polygons may be convex or star.-General properties:...
- Star polygon
- Regular polygon
- PolyhedronPolyhedronIn elementary geometry a polyhedron is a geometric solid in three dimensions with flat faces and straight edges...
- Regular polyhedronRegular polyhedronA regular polyhedron is a polyhedron whose faces are congruent regular polygons which are assembled in the same way around each vertex. A regular polyhedron is highly symmetrical, being all of edge-transitive, vertex-transitive and face-transitive - i.e. it is transitive on its flags...
(5 regular Platonic solidPlatonic solidIn geometry, a Platonic solid is a convex polyhedron that is regular, in the sense of a regular polygon. Specifically, the faces of a Platonic solid are congruent regular polygons, with the same number of faces meeting at each vertex; thus, all its edges are congruent, as are its vertices and...
s and 4 Kepler–Poinsot solids)- Uniform polyhedronUniform polyhedronA uniform polyhedron is a polyhedron which has regular polygons as faces and is vertex-transitive...
- Uniform polyhedron
- Regular polyhedron
- PolychoronPolychoronIn geometry, a polychoron or 4-polytope is a four-dimensional polytope. It is a connected and closed figure, composed of lower dimensional polytopal elements: vertices, edges, faces , and cells...
- Convex regular 4-polytopeConvex regular 4-polytopeIn mathematics, a convex regular 4-polytope is a 4-dimensional polytope that is both regular and convex. These are the four-dimensional analogs of the Platonic solids and the regular polygons ....
(6 regular polychora)- Uniform polychoronUniform polychoronIn geometry, a uniform polychoron is a polychoron or 4-polytope which is vertex-transitive and whose cells are uniform polyhedra....
- Uniform polychoron
- Schläfli–Hess polychoron (10 regular star polychora)
- Convex regular 4-polytope
- TessellationTessellationA tessellation or tiling of the plane is a pattern of plane figures that fills the plane with no overlaps and no gaps. One may also speak of tessellations of parts of the plane or of other surfaces. Generalizations to higher dimensions are also possible. Tessellations frequently appeared in the art...
- Tilings of regular polygons
- Convex uniform honeycombConvex uniform honeycombIn geometry, a convex uniform honeycomb is a uniform tessellation which fills three-dimensional Euclidean space with non-overlapping convex uniform polyhedral cells.Twenty-eight such honeycombs exist:* the familiar cubic honeycomb and 7 truncations thereof;...
- Regular polytopeRegular polytopeIn mathematics, a regular polytope is a polytope whose symmetry is transitive on its flags, thus giving it the highest degree of symmetry. All its elements or j-faces — cells, faces and so on — are also transitive on the symmetries of the polytope, and are regular polytopes of...
- Uniform polytopeUniform polytopeA uniform polytope is a vertex-transitive polytope made from uniform polytope facets of a lower dimension. Uniform polytopes of 2 dimensions are the regular polygons....
- Uniform polytope