In geometry

Geometry

Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....

, the great icosahedron is one of four Kepler-Poinsot polyhedra (nonconvex regular polyhedra), with Schläfli symbol {3,5/2} and Coxeter-Dynkin diagram

Coxeter-Dynkin diagram

In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors...

 of . It is composed of 20 intersecting triangular faces, having five triangles meeting at each vertex in a pentagram

Pentagram

A pentagram is the shape of a five-pointed star drawn with five straight strokes...

mic sequence.

Images

Transparent model	Density Polytope density In geometry, polytope density represents the number of windings of a polytope, particularly a uniform or regular polytope, around its center. It can be visually determined by counting the minimum number of facet crossings of a ray from the center to infinity...	Stellation diagram Stellation diagram In geometry, a stellation diagram or stellation pattern is a two-dimensional diagram in the plane of some face of a polyhedron, showing lines where other face planes intersect with this one. The lines cause 2D space to be divided up into regions. Regions not intersected by any further lines are...	Spherical tiling
A transparent model of the great icosahedron (See also Animation)	It has a density of 7, as shown in this cross-section.	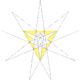It is a stellation Stellation Stellation is a process of constructing new polygons , new polyhedra in three dimensions, or, in general, new polytopes in n dimensions. The process consists of extending elements such as edges or face planes, usually in a symmetrical way, until they meet each other again...  of the icosahedron, counted by Wenninger as model [W41] and the 16th of 17 stellations of the icosahedron and 7th of 59 stellations by Coxeter.	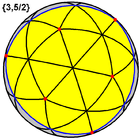This polyhedron represents a spherical tiling with a density of 7. (One spherical triangle face is shown above, outlined in blue, filled in yellow)

Related polyhedra

It shares the same vertex arrangement

Vertex arrangement

In geometry, a vertex arrangement is a set of points in space described by their relative positions. They can be described by their use in polytopes....

 as the regular convex icosahedron

Icosahedron

In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids....

. It also shares the same edge arrangement as the small stellated dodecahedron.

A truncation operation, repeatedly applied to the great icosahedron, produces a sequence of uniform polyhedra. Truncating edges down to points produces the great icosidodecahedron as a rectified great icosahedron. The process completes as a birectification, reducing the original faces down to points, and producing the great stellated dodecahedron.

The truncated

Truncation (geometry)

In geometry, a truncation is an operation in any dimension that cuts polytope vertices, creating a new facet in place of each vertex.- Uniform truncation :...

 great stellated dodecahedron is a degenerate polyhedron, with 20 triangular faces from the truncated vertices, and 12 (hidden) pentagonal faces as truncations of the original pentagram faces, the latter forming a great dodecahedron inscribed within and sharing the edges of the icosahedron.

Name	Great stellated dodecahedron	Truncated great stellated dodecahedron	Great icosidodecahedron	Truncated great icosahedron	Great icosahedron
Coxeter-Dynkin diagram Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors...
Picture

External links

• Uniform polyhedra and duals