
Order-4 pentagonal tiling
Encyclopedia
In geometry
, the order-4 pentagonal tiling is a regular tiling of the hyperbolic plane
. It has Schläfli symbol of {5,4}.
al faces, starting with the dodecahedron, with Schläfli symbol {5,n}, and Coxeter diagram , progressing to infinity.
This tiling is also topologically related as a part of sequence of regular polyhedra and tilings with four faces per vertex, starting with the octahedron
, with Schläfli symbol {n,4}, and Coxeter diagram , with n progressing to infinity.
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, the order-4 pentagonal tiling is a regular tiling of the hyperbolic plane
Hyperbolic geometry
In mathematics, hyperbolic geometry is a non-Euclidean geometry, meaning that the parallel postulate of Euclidean geometry is replaced...
. It has Schläfli symbol of {5,4}.
Related polyhedra and tiling
This tiling is topologically related as a part of sequence of regular polyhedra and tilings with pentagonPentagon
In geometry, a pentagon is any five-sided polygon. A pentagon may be simple or self-intersecting. The sum of the internal angles in a simple pentagon is 540°. A pentagram is an example of a self-intersecting pentagon.- Regular pentagons :In a regular pentagon, all sides are equal in length and...
al faces, starting with the dodecahedron, with Schläfli symbol {5,n}, and Coxeter diagram , progressing to infinity.
 {5,3} |
 {5,4} |
 {5,5} |
 {5,6} |
{5,7} |
This tiling is also topologically related as a part of sequence of regular polyhedra and tilings with four faces per vertex, starting with the octahedron
Octahedron
In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....
, with Schläfli symbol {n,4}, and Coxeter diagram , with n progressing to infinity.
 {3,4} Octahedron In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex.... |
 {4,4} |
 {5,4} |
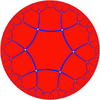 {6,4} |
 {7,4} |
... | {∞,4} |
See also
- Square tiling
- Tilings of regular polygons
- List of uniform planar tilings
- List of regular polytopes

