Heptadecagon
Encyclopedia
In geometry
, a heptadecagon (or 17-gon) is a seventeen-sided polygon
.
, as was shown by Carl Friedrich Gauss
in 1796 at the age of 19.
Constructibility implies that trigonometric function
s of can be expressed with basic arithmetic
and square root
s alone. Gauss' book Disquisitiones Arithmeticae
contains the following equation, given here in modern notation:
The first actual method of construction was devised by Johannes Erchinger, a few years after Gauss' work.
Thanks to the construction above it is easy to obtain multiples of 17 by 3 and 5 and any power of 2, for example a 34-gon, 51-gon, 85-gon or 255-gon.
Carl Friedrich Gauss proved - as a 19-year-old student at Göttingen University - that the regular heptadecagon (a 17 sided polygon) is constructible with a pair of compasses and a straightedge. His proof relies on the property of irreducible polynomial equations that roots composed of a finite number of square root extractions only exist when the order of the equation is a product of the forms
. There are distinct primes of the form :
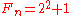, known as Fermat primes. Constructions for the regular triangle, square, pentagon, hexagon et al. had been given by Euclid, but constructions based on the Fermat primes other than 3 and 5 were unknown to the ancients. (The only known Fermat primes are 
for n = 0, 1, 2, 3, 4. They are 3, 5, 17, 257, 65537.) The first explicit construction of a heptadecagon was given by Erchinger (see above).
Another method of construction uses Carlyle circles, as shown below:
for one higher-dimensional polytope, projected in a skew orthogonal projection:
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, a heptadecagon (or 17-gon) is a seventeen-sided polygon
Polygon
In geometry a polygon is a flat shape consisting of straight lines that are joined to form a closed chain orcircuit.A polygon is traditionally a plane figure that is bounded by a closed path, composed of a finite sequence of straight line segments...
.
Heptadecagon construction
The regular heptadecagon is a constructible polygonConstructible polygon
In mathematics, a constructible polygon is a regular polygon that can be constructed with compass and straightedge. For example, a regular pentagon is constructible with compass and straightedge while a regular heptagon is not....
, as was shown by Carl Friedrich Gauss
Carl Friedrich Gauss
Johann Carl Friedrich Gauss was a German mathematician and scientist who contributed significantly to many fields, including number theory, statistics, analysis, differential geometry, geodesy, geophysics, electrostatics, astronomy and optics.Sometimes referred to as the Princeps mathematicorum...
in 1796 at the age of 19.
Constructibility implies that trigonometric function
Trigonometric function
In mathematics, the trigonometric functions are functions of an angle. They are used to relate the angles of a triangle to the lengths of the sides of a triangle...
s of can be expressed with basic arithmetic
Arithmetic
Arithmetic or arithmetics is the oldest and most elementary branch of mathematics, used by almost everyone, for tasks ranging from simple day-to-day counting to advanced science and business calculations. It involves the study of quantity, especially as the result of combining numbers...
and square root
Square root
In mathematics, a square root of a number x is a number r such that r2 = x, or, in other words, a number r whose square is x...
s alone. Gauss' book Disquisitiones Arithmeticae
Disquisitiones Arithmeticae
The Disquisitiones Arithmeticae is a textbook of number theory written in Latin by Carl Friedrich Gauss in 1798 when Gauss was 21 and first published in 1801 when he was 24...
contains the following equation, given here in modern notation:
The first actual method of construction was devised by Johannes Erchinger, a few years after Gauss' work.
Thanks to the construction above it is easy to obtain multiples of 17 by 3 and 5 and any power of 2, for example a 34-gon, 51-gon, 85-gon or 255-gon.
Carl Friedrich Gauss proved - as a 19-year-old student at Göttingen University - that the regular heptadecagon (a 17 sided polygon) is constructible with a pair of compasses and a straightedge. His proof relies on the property of irreducible polynomial equations that roots composed of a finite number of square root extractions only exist when the order of the equation is a product of the forms
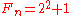. There are distinct primes of the form :, known as Fermat primes. Constructions for the regular triangle, square, pentagon, hexagon et al. had been given by Euclid, but constructions based on the Fermat primes other than 3 and 5 were unknown to the ancients. (The only known Fermat primes are for n = 0, 1, 2, 3, 4. They are 3, 5, 17, 257, 65537.) The first explicit construction of a heptadecagon was given by Erchinger (see above).Another method of construction uses Carlyle circles, as shown below:
Petrie polygons
The regular heptadecagon is the Petrie polygonPetrie polygon
In geometry, a Petrie polygon for a regular polytope of n dimensions is a skew polygon such that every consecutive sides belong to one of the facets...
for one higher-dimensional polytope, projected in a skew orthogonal projection:
16-simplex (16D) |
Further reading
- Klein, FelixFelix KleinChristian Felix Klein was a German mathematician, known for his work in group theory, function theory, non-Euclidean geometry, and on the connections between geometry and group theory...
et al. Famous Problems and Other Monographs. - Describes the algebraic aspect, by Gauss.
External links
Contains a description of the construction.- Heptadecagon trigonometric functions
- heptadecagon building New R&D center for SolarUK
- BBC video of New R&D center for SolarUK