
Uniform tessellation
Encyclopedia
In geometry
, a uniform tessellation is a vertex-transitive
tessellations made from uniform polytope facets
. All of its vertices are identical and there is the same combination and arrangement of faces at each vertex.
An n-dimensional uniform tessellation can be constructed on the surface of n-spheres, in n-dimensional Euclidean space, and n-dimensional hyperbolic space.
Nearly all uniform tessellations can be generated by a Wythoff construction
, and represented by a Coxeter-Dynkin diagram
. The terminology for the convex uniform polytopes used in uniform polyhedron
, uniform polychoron
, uniform polyteron
, uniform polypeton, uniform tiling
, and convex uniform honeycomb
articles were coined by Norman Johnson.
Wythoffian tessellations can be defined by a vertex figure
. For 2-dimensional tilings, they can be given by a vertex configuration
listing the sequence of faces around every vertex. For example 4.4.4.4 represents a regular tessellation, a square tiling, with 4 squares around each vertex. In general an n-dimensional uniform tessellation vertex figures are define by an (n-1)-polytope with edges labeled with integers, representing the number of sides of the polygonal face at each edge radiating from the vertex.
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, a uniform tessellation is a vertex-transitive
Vertex-transitive
In geometry, a polytope is isogonal or vertex-transitive if, loosely speaking, all its vertices are the same...
tessellations made from uniform polytope facets
Facet (mathematics)
A facet of a simplicial complex is a maximal simplex.In the general theory of polyhedra and polytopes, two conflicting meanings are currently jostling for acceptability:...
. All of its vertices are identical and there is the same combination and arrangement of faces at each vertex.
An n-dimensional uniform tessellation can be constructed on the surface of n-spheres, in n-dimensional Euclidean space, and n-dimensional hyperbolic space.
Nearly all uniform tessellations can be generated by a Wythoff construction
Wythoff construction
In geometry, a Wythoff construction, named after mathematician Willem Abraham Wythoff, is a method for constructing a uniform polyhedron or plane tiling. It is often referred to as Wythoff's kaleidoscopic construction.- Construction process :...
, and represented by a Coxeter-Dynkin diagram
Coxeter-Dynkin diagram
In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors...
. The terminology for the convex uniform polytopes used in uniform polyhedron
Uniform polyhedron
A uniform polyhedron is a polyhedron which has regular polygons as faces and is vertex-transitive...
, uniform polychoron
Uniform polychoron
In geometry, a uniform polychoron is a polychoron or 4-polytope which is vertex-transitive and whose cells are uniform polyhedra....
, uniform polyteron
Uniform polyteron
In geometry, a uniform polyteron is a five-dimensional uniform polytope. By definition, a uniform polyteron is vertex-transitive and constructed from uniform polychoron facets....
, uniform polypeton, uniform tiling
Uniform tiling
In geometry, a uniform tiling is a tessellation of the plane by regular polygon faces with the restriction of being vertex-uniform.Uniform tilings can exist in both the Euclidean plane and hyperbolic plane...
, and convex uniform honeycomb
Convex uniform honeycomb
In geometry, a convex uniform honeycomb is a uniform tessellation which fills three-dimensional Euclidean space with non-overlapping convex uniform polyhedral cells.Twenty-eight such honeycombs exist:* the familiar cubic honeycomb and 7 truncations thereof;...
articles were coined by Norman Johnson.
Wythoffian tessellations can be defined by a vertex figure
Vertex figure
In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:...
. For 2-dimensional tilings, they can be given by a vertex configuration
Vertex configuration
In geometry, a vertex configuration is a short-hand notation for representing the vertex figure of a polyhedron or tiling as the sequence of faces around a vertex. For uniform polyhedra there is only one vertex type and therefore the vertex configuration fully defines the polyhedron...
listing the sequence of faces around every vertex. For example 4.4.4.4 represents a regular tessellation, a square tiling, with 4 squares around each vertex. In general an n-dimensional uniform tessellation vertex figures are define by an (n-1)-polytope with edges labeled with integers, representing the number of sides of the polygonal face at each edge radiating from the vertex.
Examples
| 2-dimensional tessellations | |||
|---|---|---|---|
| Spherical | Euclidean | Hyperbolic | |
| Picture |  Truncated icosidodecahedron Truncated icosidodecahedron In geometry, the truncated icosidodecahedron is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids constructed by two or more types of regular polygon faces.... . |
 Great rhombitrihexagonal tiling Great rhombitrihexagonal tiling In geometry, the truncated trihexagonal tiling is a semiregular tiling of the Euclidean plane. There are one square, one hexagon, and one dodecagon on each vertex... . |
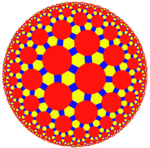 (Poincaré disk model Poincaré disk model In geometry, the Poincaré disk model, also called the conformal disk model, is a model of n-dimensional hyperbolic geometry in which the points of the geometry are in an n-dimensional disk, or unit ball, and the straight lines of the hyperbolic geometry are segments of circles contained in the disk... ) The great rhombitriheptagonal tiling is a uniform tessellation on the hyperbolic plane Hyperbolic space In mathematics, hyperbolic space is a type of non-Euclidean geometry. Whereas spherical geometry has a constant positive curvature, hyperbolic geometry has a negative curvature: every point in hyperbolic space is a saddle point... . |
| Vertex figure Vertex figure In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:... |
 |
 |
 |
| Coxeter-Dynkin Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... |
|||
| 3-dimensional tessellations | |||
| 3-spherical | 3-Euclidean | 3-hyperbolic | |
| Picture |  (Stereographic projection Stereographic projection The stereographic projection, in geometry, is a particular mapping that projects a sphere onto a plane. The projection is defined on the entire sphere, except at one point — the projection point. Where it is defined, the mapping is smooth and bijective. It is conformal, meaning that it... ) The regular 120-cell |
 The regular cubic honeycomb Cubic honeycomb The cubic honeycomb is the only regular space-filling tessellation in Euclidean 3-space, made up of cubic cells. It has 4 cubes around every edge, and 8 cubes around each vertex. Its vertex figure is a regular octahedron.... |
 (Beltrami-Klein model) The regular order-4 dodecahedral honeycomb |
| Vertex figure Vertex figure In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:... |
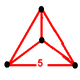 (Tetrahedron Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids... ) |
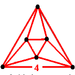 (Octahedron Octahedron In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex.... ) |
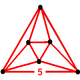 (Octahedron) |
| Coxeter-Dynkin Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... |
|||
See also
- Uniform tilingUniform tilingIn geometry, a uniform tiling is a tessellation of the plane by regular polygon faces with the restriction of being vertex-uniform.Uniform tilings can exist in both the Euclidean plane and hyperbolic plane...
- List of uniform tilings
- Uniform tilings in hyperbolic planeUniform tilings in hyperbolic planeThere are an infinite number of uniform tilings on the hyperbolic plane based on the where 1/p + 1/q + 1/r ...
- Honeycomb (geometry)Honeycomb (geometry)In geometry, a honeycomb is a space filling or close packing of polyhedral or higher-dimensional cells, so that there are no gaps. It is an example of the more general mathematical tiling or tessellation in any number of dimensions....
- Wythoff constructionWythoff constructionIn geometry, a Wythoff construction, named after mathematician Willem Abraham Wythoff, is a method for constructing a uniform polyhedron or plane tiling. It is often referred to as Wythoff's kaleidoscopic construction.- Construction process :...
- Convex uniform honeycombConvex uniform honeycombIn geometry, a convex uniform honeycomb is a uniform tessellation which fills three-dimensional Euclidean space with non-overlapping convex uniform polyhedral cells.Twenty-eight such honeycombs exist:* the familiar cubic honeycomb and 7 truncations thereof;...
- List of regular polytopes

