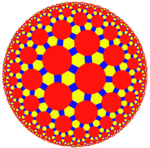
Great rhombitriheptagonal tiling
Encyclopedia
In geometry
, the truncated triheptagonal tiling is a semiregular tiling of the hyperbolic plane. There are one square
, one hexagon, and one tetrakaidecagon (14-sides) on each vertex
. It has Schläfli symbol of t0,1,2{7,3}.
s of a truncated triheptagonal tiling. (Naming the colors by indices around a vertex: 123.)
polyhedra with vertex figure
(4.6.2n). This set of polyhedra are zonohedron
s.
Each triangle in this dual tiling represent a fundamental domain of the Wythoff construction
for the symmetry group [7,3].
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, the truncated triheptagonal tiling is a semiregular tiling of the hyperbolic plane. There are one square
Square (geometry)
In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles...
, one hexagon, and one tetrakaidecagon (14-sides) on each vertex
Vertex (geometry)
In geometry, a vertex is a special kind of point that describes the corners or intersections of geometric shapes.-Of an angle:...
. It has Schläfli symbol of t0,1,2{7,3}.
Iniform colorings
There is only one uniform coloringUniform coloring
In geometry, a uniform coloring is a property of a uniform figure that is colored to be vertex-transitive...
s of a truncated triheptagonal tiling. (Naming the colors by indices around a vertex: 123.)
Related polyhedra and tilings
This tiling is topologically related as a part of sequence of omnitruncatedOmnitruncation (geometry)
In geometry, an omnitruncation is an operation applied to a regular polytope in a Wythoff construction that creates a maximum number of facets...
polyhedra with vertex figure
Vertex figure
In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:...
(4.6.2n). This set of polyhedra are zonohedron
Zonohedron
A zonohedron is a convex polyhedron where every face is a polygon with point symmetry or, equivalently, symmetry under rotations through 180°. Any zonohedron may equivalently be described as the Minkowski sum of a set of line segments in three-dimensional space, or as the three-dimensional...
s.
 (4.6.4) Hexagonal prism In geometry, the hexagonal prism is a prism with hexagonal base. The shape has 8 faces, 18 edges, and 12 vertices.Since it has eight faces, it is an octahedron. However, the term octahedron is primarily used to refer to the regular octahedron, which has eight triangular faces... |
 (4.6.6) Truncated octahedron In geometry, the truncated octahedron is an Archimedean solid. It has 14 faces , 36 edges, and 24 vertices. Since each of its faces has point symmetry the truncated octahedron is a zonohedron.... |
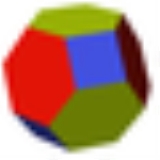
 (4.6.8) Truncated cuboctahedron In geometry, the truncated cuboctahedron is an Archimedean solid. It has 12 square faces, 8 regular hexagonal faces, 6 regular octagonal faces, 48 vertices and 72 edges... |
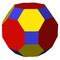
 (4.6.10) Truncated icosidodecahedron In geometry, the truncated icosidodecahedron is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids constructed by two or more types of regular polygon faces.... |
 (4.6.12) |
 (4.6.14) |
 (4.6.16) |
(4.6.∞) |
Dual tiling
The dual tiling is called an order-3 bisected heptagonal tiling, made as a complete bisection of the order-3 heptagonal tiling, here with triangles colored alternatingly white and blue.Each triangle in this dual tiling represent a fundamental domain of the Wythoff construction
Wythoff construction
In geometry, a Wythoff construction, named after mathematician Willem Abraham Wythoff, is a method for constructing a uniform polyhedron or plane tiling. It is often referred to as Wythoff's kaleidoscopic construction.- Construction process :...
for the symmetry group [7,3].


