Exceptional object
Encyclopedia
Many branches of mathematics study objects of a given type and prove a classification theorem
. A common theme is that the classification results in a number of series of objects as well as a finite number of exceptions that don't fit into any series. These are known as exceptional objects.
Frequently these exceptional objects play a further and important role in the subject. Surprisingly, the exceptional objects in one branch of mathematics are often related to the exceptional objects in others.
A related phenomenon is exceptional isomorphism
, when two series are in general different, but agree for some small values.
s. In 2 dimensions we have a series of regular n-gons
for n ≥ 3. In every dimension above 2 we find analogues of the cube, tetrahedron and octahedron. In 3 dimensions we find two more regular polyhedra – the dodecahedron (12-cell) and the icosahedron
(20-cell) – making 5 Platonic solids. In 4 dimensions we have a total of 6 regular polytopes
including the 120-cell, the 600-cell and the 24-cell. There are no other regular polytopes; in higher dimensions the only regular polytopes are of the hypercube
, simplex
, orthoplex series. So we have three series and 5 exceptional polytopes.
The pattern is similar if non-convex polytopes are included. In two dimensions there is a regular star polygon for every rational number
p/q > 2. In three dimensions there are four Kepler–Poinsot polyhedra, and in four dimensions ten Schläfli–Hess polychora; in higher dimensions there are no non-convex regular figures.
These can be generalized to tessellation
s of other spaces, especially uniform tessellation
s, notably tilings of Euclidean space (honeycombs
), which have exceptional objects, and tilings of hyperbolic space. There are various exceptional objects in dimension below 6, but in dimension 6 and above the only regular polyhedra/tilings/hyperbolic tilings are the simplex, hypercube, cross-polytope, and hypercube lattice.
Related to tilings and the regular polyhedra, there are exceptional Schwarz triangle
s (triangles that tile the sphere, or more generally Euclidean plane or hyperbolic plane via their triangle group
of reflections in their edges), particularly the Möbius triangles. In the sphere there are 3 Möbius triangles (and 1 1-parameter family), corresponding to the 3 exceptional Platonic solid groups, while in the Euclidean plane there are 3 Möbius triangles, corresponding to the 3 special triangles: 60-60-60 (equilateral), 45-45-90 (isosceles right), and 30-60-90. There are additional exceptional Schwartz triangles in the sphere and Euclidean plane. By contrast, in the hyperbolic plane there is a 3-parameter family of Möbius triangles, and none exceptional.
The finite simple groups have been classified
into a number of series as well as 26 sporadic groups. Of these, 20 are subgroups or subquotients of the monster group
, referred to as the "Happy Family", while 6 are not, and are referred to as "pariahs
".
Several of the sporadic groups are related to the Leech lattice, most notably the Conway group Co1, which is the automorphism group of the Leech lattice, quotiented out by its center.
is the Albert algebra
of 3 by 3 self-adjoint matrices over the octonions.
s form a number of series (classical Lie groups) labelled A, B, C and D. In addition we have the exceptional groups G2 (the automorphism group of the octonions), F4, E6, E7, E8
. These last four groups can be viewed as the symmetry groups of projective planes over O, C⊗O, H⊗O and O⊗O respectively, where O is the octonions and the tensor products are over the reals.
The classification of Lie groups corresponds to the classification of root systems and so the exceptional Lie groups correspond to exceptional root systems and exceptional Dynkin diagrams.
. The Lie superalgebra
s G(3) in 31 dimensions and F(4) in 40 dimensions and the Jordan superalgebras K3 and K10 being the main finite dimensional examples.
in 15 dimensions or less — the E8 lattice
. Up to dimension 24
there is only one even unimodular lattice with no roots
, the Leech lattice
. Three of the sporadic simple groups were discovered by Conway while investigating the automorphism group of the Leech lattice. For example Co1
is the automorphism group itself modulo ±1. The groups Co2
and Co3
, as well as a number of other sporadic groups, arise as stabilisers of various subsets of the Leech lattice.
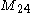, one of the sporadic simple groups, is the group of automorphisms of the extended binary Golay code
and four more of the sporadic simple groups arise as various types of stabilizer subgroup of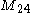
.
S(5,8,24) whose automorphism group is the sporadic simple Mathieu group
.
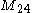, but in particular cases they have other, exceptional outer automorphisms.
Among families of finite simple groups, the only example is in the automorphisms of the symmetric and alternating groups: for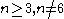
the alternating group 
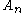has one outer automorphism (corresponding to conjugation by an odd element of 
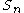) and the symmetric group
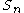has no outer automorphisms. However, for 
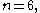there is an exceptional outer automorphism of 
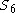(of order 2), and correspondingly, the outer automorphism group of 
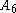is not 
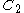(the group of order 2) but rather 
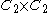(the Klein four-group
).
If one instead considers A6 as the (isomorphic) projective special linear group PSL(2,9), then the outer automorphism is not exceptional; thus the exceptionalness can be seen as due to the exceptional isomorphism
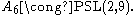This exceptional outer automorphism is realized inside of the Mathieu group M12 and similarly, M12 acts on a set of 12 elements in 2 different ways.
Among Lie groups, the spin group Spin(8) has an exceptionally large outer automorphism group (namely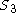 
), which corresponds to the exceptional symmetries of the Dynkin diagram D4. This phenomenon is referred to as triality
.
The exceptional symmetry of the D4 diagram also gives rise to the Steinberg group
s.
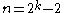for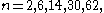 
and possibly 126, but no higher, are exceptional objects related to exotic sphere
s.
dimensions, noting that 24 = 8 · 3. By contrast, the pariah group
s stand apart, as the name suggests.
, 8-fold real Bott periodicity can be seen as coming from the octonions. In the theory of modular forms, the 24-dimensional nature of the Leech lattice underlies the presence of 24 in the formulas for the Dedekind eta function
and the modular discriminant, which connection is deepened by monstrous moonshine
, which related modular functions to the monster group.
and superstring theory we often find that particular dimensions are singled out as a result of exceptional algebraic phenomena. For example, bosonic string theory
requires a spacetime of dimension 26 which is directly related to the presence of 24 in the Dedekind eta function
. Similarly, the possible dimensions of supergravity
are related to the dimensions of the division algebras.
, such as nowhere differentiable functions, or "exotic", as in exotic sphere
s – there are exotic spheres in arbitrarily high dimension (not only a finite set of exceptions), and in many dimensions most (differential structures on) spheres are exotic.
φ has the simplest continued fraction
approximation, and accordingly is most difficult to approximate by rationals
; however, it is but one of infinitely many such quadratic numbers (continued fractions).
Similarly, the (2,3,7) Schwarz triangle
is the smallest hyperbolic Schwarz triangle, and the associated (2,3,7) triangle group
is of particular interest, being the universal Hurwitz group, and thus being associated with the Hurwitz curves, the maximally symmetric algebraic curves. However, it falls in a family of such triangles ((2,4,7), (2,3,8), (3,3,7), etc.), and while the smallest, is not exceptional or unlike the others.
conjectures show how, for example, the Monster group
is connected to String Theory
. The theory of modular forms shows how the E8 is connected to the Monster group. Other interesting connections include how the Leech lattice
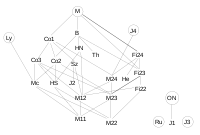
is connected via the Golay code to the adjacency matrix of the dodecahedron (another exceptional object). Below is a mind map
showing how some of the exceptional objects in mathematical physics are related.
The connections can partly be explained by thinking of the algebras as a tower of lattice vertex operator algebra
s. It just so happens that the vertex algebras at the bottom are so simple that they are isomorphic to familiar non-vertex algebras. Thus the connections can be seen simply as the consequence of some lattices being sub-lattices of others.
. These are the Lie superalgebra
s which are related to Lorentzian lattices. This subject is less developed so the connections between the objects is less developed. There are new conjectures parallel to the Monstrous moonshine
conjectures for these super-objects involving different sporadic groups.
Classification theorem
In mathematics, a classification theorem answers the classification problem "What are the objects of a given type, up to some equivalence?". It gives a non-redundant enumeration: each object is equivalent to exactly one class....
. A common theme is that the classification results in a number of series of objects as well as a finite number of exceptions that don't fit into any series. These are known as exceptional objects.
Frequently these exceptional objects play a further and important role in the subject. Surprisingly, the exceptional objects in one branch of mathematics are often related to the exceptional objects in others.
A related phenomenon is exceptional isomorphism
Exceptional isomorphism
In mathematics, an exceptional isomorphism, also called an accidental isomorphism, is an isomorphism between members ai and bj of two families of mathematical objects, that is not an example of a pattern of such isomorphisms.Because these series of objects are presented differently, they are not...
, when two series are in general different, but agree for some small values.
Regular polytopes
The prototypical examples of exceptional objects arise when we classify the regular polytopeRegular polytope
In mathematics, a regular polytope is a polytope whose symmetry is transitive on its flags, thus giving it the highest degree of symmetry. All its elements or j-faces — cells, faces and so on — are also transitive on the symmetries of the polytope, and are regular polytopes of...
s. In 2 dimensions we have a series of regular n-gons
Regular polygon
A regular polygon is a polygon that is equiangular and equilateral . Regular polygons may be convex or star.-General properties:...
for n ≥ 3. In every dimension above 2 we find analogues of the cube, tetrahedron and octahedron. In 3 dimensions we find two more regular polyhedra – the dodecahedron (12-cell) and the icosahedron
Icosahedron
In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids....
(20-cell) – making 5 Platonic solids. In 4 dimensions we have a total of 6 regular polytopes
Convex regular 4-polytope
In mathematics, a convex regular 4-polytope is a 4-dimensional polytope that is both regular and convex. These are the four-dimensional analogs of the Platonic solids and the regular polygons ....
including the 120-cell, the 600-cell and the 24-cell. There are no other regular polytopes; in higher dimensions the only regular polytopes are of the hypercube
Hypercube
In geometry, a hypercube is an n-dimensional analogue of a square and a cube . It is a closed, compact, convex figure whose 1-skeleton consists of groups of opposite parallel line segments aligned in each of the space's dimensions, perpendicular to each other and of the same length.An...
, simplex
Simplex
In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...
, orthoplex series. So we have three series and 5 exceptional polytopes.
The pattern is similar if non-convex polytopes are included. In two dimensions there is a regular star polygon for every rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
p/q > 2. In three dimensions there are four Kepler–Poinsot polyhedra, and in four dimensions ten Schläfli–Hess polychora; in higher dimensions there are no non-convex regular figures.
These can be generalized to tessellation
Tessellation
A tessellation or tiling of the plane is a pattern of plane figures that fills the plane with no overlaps and no gaps. One may also speak of tessellations of parts of the plane or of other surfaces. Generalizations to higher dimensions are also possible. Tessellations frequently appeared in the art...
s of other spaces, especially uniform tessellation
Uniform tessellation
In geometry, a uniform tessellation is a vertex-transitive tessellations made from uniform polytope facets. All of its vertices are identical and there is the same combination and arrangement of faces at each vertex....
s, notably tilings of Euclidean space (honeycombs
Honeycomb (geometry)
In geometry, a honeycomb is a space filling or close packing of polyhedral or higher-dimensional cells, so that there are no gaps. It is an example of the more general mathematical tiling or tessellation in any number of dimensions....
), which have exceptional objects, and tilings of hyperbolic space. There are various exceptional objects in dimension below 6, but in dimension 6 and above the only regular polyhedra/tilings/hyperbolic tilings are the simplex, hypercube, cross-polytope, and hypercube lattice.
Schwartz triangles
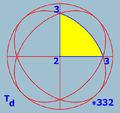 (3 3 2) |
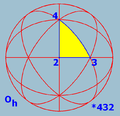 (4 3 2) |
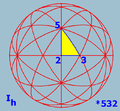 (5 3 2) |
 (3 3 3) |
 (4 4 2) |
 (6 3 2) |
Related to tilings and the regular polyhedra, there are exceptional Schwarz triangle
Schwarz triangle
In geometry, a Schwarz triangle, named after Hermann Schwarz is a spherical triangle that can be used to tile a sphere, possibly overlapping, through reflections in its edges. They were classified in ....
s (triangles that tile the sphere, or more generally Euclidean plane or hyperbolic plane via their triangle group
Triangle group
In mathematics, a triangle group is a group that can be realized geometrically by sequences of reflections across the sides of a triangle. The triangle can be an ordinary Euclidean triangle, a triangle on the sphere, or a hyperbolic triangle...
of reflections in their edges), particularly the Möbius triangles. In the sphere there are 3 Möbius triangles (and 1 1-parameter family), corresponding to the 3 exceptional Platonic solid groups, while in the Euclidean plane there are 3 Möbius triangles, corresponding to the 3 special triangles: 60-60-60 (equilateral), 45-45-90 (isosceles right), and 30-60-90. There are additional exceptional Schwartz triangles in the sphere and Euclidean plane. By contrast, in the hyperbolic plane there is a 3-parameter family of Möbius triangles, and none exceptional.
Finite simple groups
Classification of finite simple groups
In mathematics, the classification of the finite simple groups is a theorem stating that every finite simple group belongs to one of four categories described below. These groups can be seen as the basic building blocks of all finite groups, in much the same way as the prime numbers are the basic...
into a number of series as well as 26 sporadic groups. Of these, 20 are subgroups or subquotients of the monster group
Monster group
In the mathematical field of group theory, the Monster group M or F1 is a group of finite order:...
, referred to as the "Happy Family", while 6 are not, and are referred to as "pariahs
Pariah group
In mathematical group theory, the term pariah was introduced by to refer to the six sporadic simple groups that are not subquotients of the monster simple group.These groups are:*Three of the Janko groups: J1, J3, and J4.*The Lyons group...
".
Several of the sporadic groups are related to the Leech lattice, most notably the Conway group Co1, which is the automorphism group of the Leech lattice, quotiented out by its center.
Division algebras
There are only three associative division algebras over the reals - the real numbers, the complex numbers and the quaternions. The only non-associative division algebra is the algebra of octonions. The octonions are connected to a wide variety of exceptional objects. For example the exceptional formally real Jordan algebraJordan algebra
In abstract algebra, a Jordan algebra is an algebra over a field whose multiplication satisfies the following axioms:# xy = yx # = x ....
is the Albert algebra
Albert algebra
In mathematics, an Albert algebra is a 27-dimensional exceptional Jordan algebra. They are named after Abraham Adrian Albert, who pioneered the study of non-associative algebras, usually working over the real numbers. Over the real numbers, there are two such Jordan algebras up to isomorphism...
of 3 by 3 self-adjoint matrices over the octonions.
Simple Lie groups
The simple Lie groupSimple Lie group
In group theory, a simple Lie group is a connected non-abelian Lie group G which does not have nontrivial connected normal subgroups.A simple Lie algebra is a non-abelian Lie algebra whose only ideals are 0 and itself...
s form a number of series (classical Lie groups) labelled A, B, C and D. In addition we have the exceptional groups G2 (the automorphism group of the octonions), F4, E6, E7, E8
E8 (mathematics)
In mathematics, E8 is any of several closely related exceptional simple Lie groups, linear algebraic groups or Lie algebras of dimension 248; the same notation is used for the corresponding root lattice, which has rank 8...
. These last four groups can be viewed as the symmetry groups of projective planes over O, C⊗O, H⊗O and O⊗O respectively, where O is the octonions and the tensor products are over the reals.
The classification of Lie groups corresponds to the classification of root systems and so the exceptional Lie groups correspond to exceptional root systems and exceptional Dynkin diagrams.
Supersymmetric algebras
There are a few exceptional objects with supersymmetrySupersymmetry
In particle physics, supersymmetry is a symmetry that relates elementary particles of one spin to other particles that differ by half a unit of spin and are known as superpartners...
. The Lie superalgebra
Lie superalgebra
In mathematics, a Lie superalgebra is a generalisation of a Lie algebra to include a Z2-grading. Lie superalgebras are important in theoretical physics where they are used to describe the mathematics of supersymmetry...
s G(3) in 31 dimensions and F(4) in 40 dimensions and the Jordan superalgebras K3 and K10 being the main finite dimensional examples.
Unimodular lattices
Up to isometry there is only one even unimodular latticeUnimodular lattice
In mathematics, a unimodular lattice is a lattice of determinant 1 or −1.The E8 lattice and the Leech lattice are two famous examples.- Definitions :...
in 15 dimensions or less — the E8 lattice
E8 lattice
In mathematics, the E8 lattice is a special lattice in R8. It can be characterized as the unique positive-definite, even, unimodular lattice of rank 8...
. Up to dimension 24
24 (number)
24 is the natural number following 23 and preceding 25.The SI prefix for 1024 is yotta , and for 10−24 yocto...
there is only one even unimodular lattice with no roots
Root system
In mathematics, a root system is a configuration of vectors in a Euclidean space satisfying certain geometrical properties. The concept is fundamental in the theory of Lie groups and Lie algebras...
, the Leech lattice
Leech lattice
In mathematics, the Leech lattice is an even unimodular lattice Λ24 in 24-dimensional Euclidean space E24 found by .-History:Many of the cross-sections of the Leech lattice, including the Coxeter–Todd lattice and Barnes–Wall lattice, in 12 and 16 dimensions, were found much earlier than...
. Three of the sporadic simple groups were discovered by Conway while investigating the automorphism group of the Leech lattice. For example Co1
Conway group
In mathematics, the Conway groups Co1, Co2, and Co3 are three sporadic groups discovered by John Horton Conway.The largest of the Conway groups, Co1, of order...
is the automorphism group itself modulo ±1. The groups Co2
Conway group
In mathematics, the Conway groups Co1, Co2, and Co3 are three sporadic groups discovered by John Horton Conway.The largest of the Conway groups, Co1, of order...
and Co3
Conway group
In mathematics, the Conway groups Co1, Co2, and Co3 are three sporadic groups discovered by John Horton Conway.The largest of the Conway groups, Co1, of order...
, as well as a number of other sporadic groups, arise as stabilisers of various subsets of the Leech lattice.
Codes
Some codes also stand out as exceptional objects, in particular the perfect binary Golay code which is closely related to the Leech lattice. The Mathieu group, one of the sporadic simple groups, is the group of automorphisms of the extended binary Golay codeBinary Golay code
In mathematics and electronics engineering, a binary Golay code is a type of error-correcting code used in digital communications. The binary Golay code, along with the ternary Golay code, has a particularly deep and interesting connection to the theory of finite sporadic groups in mathematics....
and four more of the sporadic simple groups arise as various types of stabilizer subgroup of
.Block designs
An exceptional block design is the Steiner systemSteiner system
250px|right|thumbnail|The [[Fano plane]] is an S Steiner triple system. The blocks are the 7 lines, each containing 3 points. Every pair of points belongs to a unique line....
S(5,8,24) whose automorphism group is the sporadic simple Mathieu group
Mathieu group
In the mathematical field of group theory, the Mathieu groups, named after the French mathematician Émile Léonard Mathieu, are five finite simple groups he discovered and reported in papers in 1861 and 1873; these were the first sporadic simple groups discovered...
.Outer automorphisms
Certain families of groups generically have a certain outer automorphism groupOuter automorphism group
In mathematics, the outer automorphism group of a group Gis the quotient Aut / Inn, where Aut is the automorphism group of G and Inn is the subgroup consisting of inner automorphisms. The outer automorphism group is usually denoted Out...
, but in particular cases they have other, exceptional outer automorphisms.
Among families of finite simple groups, the only example is in the automorphisms of the symmetric and alternating groups: for
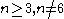the alternating group 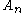has one outer automorphism (corresponding to conjugation by an odd element of 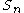) and the symmetric groupSymmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
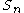has no outer automorphisms. However, for 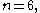there is an exceptional outer automorphism of 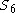(of order 2), and correspondingly, the outer automorphism group of 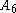is not 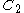(the group of order 2) but rather 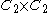(the Klein four-groupKlein four-group
In mathematics, the Klein four-group is the group Z2 × Z2, the direct product of two copies of the cyclic group of order 2...
).
If one instead considers A6 as the (isomorphic) projective special linear group PSL(2,9), then the outer automorphism is not exceptional; thus the exceptionalness can be seen as due to the exceptional isomorphism
Exceptional isomorphism
In mathematics, an exceptional isomorphism, also called an accidental isomorphism, is an isomorphism between members ai and bj of two families of mathematical objects, that is not an example of a pattern of such isomorphisms.Because these series of objects are presented differently, they are not...
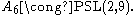This exceptional outer automorphism is realized inside of the Mathieu group M12 and similarly, M12 acts on a set of 12 elements in 2 different ways.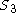), which corresponds to the exceptional symmetries of the Dynkin diagram D4. This phenomenon is referred to as trialityTriality
In mathematics, triality is a relationship between three vector spaces, analogous to the duality relation between dual vector spaces. Most commonly, it describes those special features of the Dynkin diagram D4 and the associated Lie group Spin, the double cover of 8-dimensional rotation group SO,...
.
The exceptional symmetry of the D4 diagram also gives rise to the Steinberg group
Steinberg group
In mathematics, Steinberg group means either of two distinct, though related, constructions of the mathematician Robert Steinberg:*Steinberg group St in algebraic K-theory.*Steinberg group is a 'twisted' group of Lie type....
s.
Algebraic topology
The five or six (depending on the status of n=126) (framed cobordism classes of) manifolds of Kervaire invariant one, which exist in dimension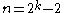 for 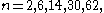and possibly 126, but no higher, are exceptional objects related to exotic sphereExotic sphere
In differential topology, a mathematical discipline, an exotic sphere is a differentiable manifold M that is homeomorphic but not diffeomorphic to the standard Euclidean n-sphere...
s.
Connections
Numerous connections have been observed between some, though not all, of these exceptional objects. Most common are objects related to 8 and 2424 (number)
24 is the natural number following 23 and preceding 25.The SI prefix for 1024 is yotta , and for 10−24 yocto...
dimensions, noting that 24 = 8 · 3. By contrast, the pariah group
Pariah group
In mathematical group theory, the term pariah was introduced by to refer to the six sporadic simple groups that are not subquotients of the monster simple group.These groups are:*Three of the Janko groups: J1, J3, and J4.*The Lyons group...
s stand apart, as the name suggests.
8 dimensions
- The octonions are 8-dimensional.
- The E8 latticeE8 latticeIn mathematics, the E8 lattice is a special lattice in R8. It can be characterized as the unique positive-definite, even, unimodular lattice of rank 8...
can be realized as the integral octonions (up to a scale factor). - The exceptional Lie groups can be seen as symmetries of the octonions and structures derived from the octonions; further, the E8 algebra is related to the E8 lattice, as the notation implies (the lattice is generated by the root system of the algebra).
- Triality occurs for Spin(8), which also connects to 8 · 3 = 24.
24 dimensions
- The Leech lattice is 24-dimensional.
- Most sporadic simple groups can be related to the Leech lattice, or more broadly the monster.
- The exceptional Jordan algebraJordan algebraIn abstract algebra, a Jordan algebra is an algebra over a field whose multiplication satisfies the following axioms:# xy = yx # = x ....
has a representation in terms of 24×24 real matrices together with the Jordan product rule.
Other phenomena
These objects are connected to various other phenomena in math which may be considered surprising but not themselves "exceptional". For example, in algebraic topologyAlgebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
, 8-fold real Bott periodicity can be seen as coming from the octonions. In the theory of modular forms, the 24-dimensional nature of the Leech lattice underlies the presence of 24 in the formulas for the Dedekind eta function
Dedekind eta function
The Dedekind eta function, named after Richard Dedekind, is a function defined on the upper half-plane of complex numbers, where the imaginary part is positive...
and the modular discriminant, which connection is deepened by monstrous moonshine
Monstrous moonshine
In mathematics, monstrous moonshine, or moonshine theory, is a term devised by John Horton Conway and Simon P. Norton in 1979, used to describe the connection between the monster group M and modular functions .- History :Specifically, Conway and Norton, following an initial observationby John...
, which related modular functions to the monster group.
Physics
In string theoryString theory
String theory is an active research framework in particle physics that attempts to reconcile quantum mechanics and general relativity. It is a contender for a theory of everything , a manner of describing the known fundamental forces and matter in a mathematically complete system...
and superstring theory we often find that particular dimensions are singled out as a result of exceptional algebraic phenomena. For example, bosonic string theory
Bosonic string theory
Bosonic string theory is the original version of string theory, developed in the late 1960s.In the early 1970s, supersymmetry was discovered in the context of string theory, and a new version of string theory called superstring theory became the real focus...
requires a spacetime of dimension 26 which is directly related to the presence of 24 in the Dedekind eta function
Dedekind eta function
The Dedekind eta function, named after Richard Dedekind, is a function defined on the upper half-plane of complex numbers, where the imaginary part is positive...
. Similarly, the possible dimensions of supergravity
Supergravity
In theoretical physics, supergravity is a field theory that combines the principles of supersymmetry and general relativity. Together, these imply that, in supergravity, the supersymmetry is a local symmetry...
are related to the dimensions of the division algebras.
Pathologies
"Exceptional" object is reserved for objects that are unusual, meaning rare, the exception, not for unexpected or non-standard objects. These unexpected-but-typical (or common) phenomena are generally referred to as pathologicalPathological (mathematics)
In mathematics, a pathological phenomenon is one whose properties are considered atypically bad or counterintuitive; the opposite is well-behaved....
, such as nowhere differentiable functions, or "exotic", as in exotic sphere
Exotic sphere
In differential topology, a mathematical discipline, an exotic sphere is a differentiable manifold M that is homeomorphic but not diffeomorphic to the standard Euclidean n-sphere...
s – there are exotic spheres in arbitrarily high dimension (not only a finite set of exceptions), and in many dimensions most (differential structures on) spheres are exotic.
Extremal objects
Exceptional objects must be distinguished from extremal objects: those that fall in a family and are the most extreme example by some measure are of interest, but not unusual in the way exceptional objects are. For example, the golden ratioGolden ratio
In mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. The golden ratio is an irrational mathematical constant, approximately 1.61803398874989...
φ has the simplest continued fraction
Continued fraction
In mathematics, a continued fraction is an expression obtained through an iterative process of representing a number as the sum of its integer part and the reciprocal of another number, then writing this other number as the sum of its integer part and another reciprocal, and so on...
approximation, and accordingly is most difficult to approximate by rationals
Diophantine approximation
In number theory, the field of Diophantine approximation, named after Diophantus of Alexandria, deals with the approximation of real numbers by rational numbers....
; however, it is but one of infinitely many such quadratic numbers (continued fractions).
Similarly, the (2,3,7) Schwarz triangle
Schwarz triangle
In geometry, a Schwarz triangle, named after Hermann Schwarz is a spherical triangle that can be used to tile a sphere, possibly overlapping, through reflections in its edges. They were classified in ....
is the smallest hyperbolic Schwarz triangle, and the associated (2,3,7) triangle group
(2,3,7) triangle group
In the theory of Riemann surfaces and hyperbolic geometry, the triangle group is particularly important. This importance stems from its connection to Hurwitz surfaces, namely Riemann surfaces of genus g with the largest possible order, 84, of its automorphism group.A note on terminology – the "...
is of particular interest, being the universal Hurwitz group, and thus being associated with the Hurwitz curves, the maximally symmetric algebraic curves. However, it falls in a family of such triangles ((2,4,7), (2,3,8), (3,3,7), etc.), and while the smallest, is not exceptional or unlike the others.
Connections
Many of the exceptional objects in mathematics and physics have been found to be connected to each other. Conjectures such as the Monstrous moonshineMonstrous moonshine
In mathematics, monstrous moonshine, or moonshine theory, is a term devised by John Horton Conway and Simon P. Norton in 1979, used to describe the connection between the monster group M and modular functions .- History :Specifically, Conway and Norton, following an initial observationby John...
conjectures show how, for example, the Monster group
Monster group
In the mathematical field of group theory, the Monster group M or F1 is a group of finite order:...
is connected to String Theory
String theory
String theory is an active research framework in particle physics that attempts to reconcile quantum mechanics and general relativity. It is a contender for a theory of everything , a manner of describing the known fundamental forces and matter in a mathematically complete system...
. The theory of modular forms shows how the E8 is connected to the Monster group. Other interesting connections include how the Leech lattice
Leech lattice
In mathematics, the Leech lattice is an even unimodular lattice Λ24 in 24-dimensional Euclidean space E24 found by .-History:Many of the cross-sections of the Leech lattice, including the Coxeter–Todd lattice and Barnes–Wall lattice, in 12 and 16 dimensions, were found much earlier than...
is connected via the Golay code to the adjacency matrix of the dodecahedron (another exceptional object). Below is a mind map
Mind map
A mind map is a diagram used to represent words, ideas, tasks, or other items linked to and arranged around a central key word or idea. Especially in British English, the terms spidergram and spidergraph are more common, but they can cause confusion with the term spider diagram used in mathematics...
showing how some of the exceptional objects in mathematical physics are related.
The connections can partly be explained by thinking of the algebras as a tower of lattice vertex operator algebra
Vertex operator algebra
In mathematics, a vertex operator algebra is an algebraic structure that plays an important role in conformal field theory and related areas of physics...
s. It just so happens that the vertex algebras at the bottom are so simple that they are isomorphic to familiar non-vertex algebras. Thus the connections can be seen simply as the consequence of some lattices being sub-lattices of others.
Supersymmetries
The Jordan superalgebras are a parallel set of exceptional objects with supersymmetrySupersymmetry
In particle physics, supersymmetry is a symmetry that relates elementary particles of one spin to other particles that differ by half a unit of spin and are known as superpartners...
. These are the Lie superalgebra
Lie superalgebra
In mathematics, a Lie superalgebra is a generalisation of a Lie algebra to include a Z2-grading. Lie superalgebras are important in theoretical physics where they are used to describe the mathematics of supersymmetry...
s which are related to Lorentzian lattices. This subject is less developed so the connections between the objects is less developed. There are new conjectures parallel to the Monstrous moonshine
Monstrous moonshine
In mathematics, monstrous moonshine, or moonshine theory, is a term devised by John Horton Conway and Simon P. Norton in 1979, used to describe the connection between the monster group M and modular functions .- History :Specifically, Conway and Norton, following an initial observationby John...
conjectures for these super-objects involving different sporadic groups.