In mathematics

• 24 is the factorial
  Factorial
  In mathematics, the factorial of a non-negative integer n, denoted by n!, is the product of all positive integers less than or equal to n...
  
   of 4 and a composite number
  Composite number
  A composite number is a positive integer which has a positive divisor other than one or itself. In other words a composite number is any positive integer greater than one that is not a prime number....
  
  , being the first number of the form , where 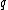is an odd prime.
• It is the smallest number with exactly eight divisor
  Divisor
  In mathematics, a divisor of an integer n, also called a factor of n, is an integer which divides n without leaving a remainder.-Explanation:...
  
  s: 1, 2, 3, 4, 6, 8, 12
  12 (number)
  12 is the natural number following 11 and preceding 13.The word "twelve" is the largest number with a single-morpheme name in English. Etymology suggests that "twelve" arises from the Germanic compound twalif "two-leftover", so a literal translation would yield "two remaining [after having ten...
  
  , and 24. It is a highly composite number
  Highly composite number
  A highly composite number is a positive integer with more divisors than any positive integer smaller than itself.The initial or smallest twenty-one highly composite numbers are listed in the table at right....
  
  , having more divisors than any smaller number. Adding up all the proper divisors of 24 except 4 and 8 gives 24, hence 24 is a semiperfect number
  Semiperfect number
  In number theory, a semiperfect number or pseudoperfect number is a natural number n that is equal to the sum of all or some of its proper divisors. A semiperfect number that is equal to the sum of all its proper divisors is a perfect number....
  
  .
• Subtracting one from any of its divisors (except 1 and 2, but including itself) yields a prime number
  Prime number
  A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
  
  . 24 is the largest number with this property, for to have this property a number cannot be divisible by a prime greater than three, nor can it be divisible by 9 or 16.
• 24 has an aliquot sum of 36 and the aliquot sequence
  Aliquot sequence
  In mathematics, an aliquot sequence is a recursive sequence in which each term is the sum of the proper divisors of the previous term. The aliquot sequence starting with a positive integer k can be defined formally in terms of the sum-of-divisors function σ1 in the following way:For example, the...
  
   (24,36,55,17,1,0). Only one number has an aliquot sum 24; 529, the square of 23
  23 (number)
  23 is the natural number following 22 and preceding 24.- In mathematics :Twenty-three is the ninth prime number, the smallest odd prime that is not a twin prime. Twenty-three is also the fifth factorial prime, the third Woodall prime...
  
  .
• There are 10 solutions to the equation φ
  Euler's totient function
  In number theory, the totient \varphi of a positive integer n is defined to be the number of positive integers less than or equal to n that are coprime to n In number theory, the totient \varphi(n) of a positive integer n is defined to be the number of positive integers less than or equal to n that...
  
  (x) = 24, namely 35, 39, 45, 52, 56, 70, 72, 78, 84 and 90. This is more than any integer below 24, making 24 a highly totient number
  Highly totient number
  A highly totient number k is an integer that has more solutions to the equation φ = k, where φ is Euler's totient function, than any integer below it. The first few highly totient numbers are...
  
  .
• 24 is a nonagonal number. This number is also the sum of a twin prime
  Twin prime
  A twin prime is a prime number that differs from another prime number by two. Except for the pair , this is the smallest possible difference between two primes. Some examples of twin prime pairs are , , , , and...
  
   (11 + 13). It is a Harshad number
  Harshad number
  A Harshad number, or Niven number in a given number base, is an integer that is divisible by the sum of its digits when written in that base. Harshad numbers were defined by D. R. Kaprekar, a mathematician from India. The word "Harshad" comes from the Sanskrit + , meaning joy-giver. The Niven...
  
   and a semi-meandric number.
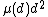• Together with the number one, 24 is one of the few numbers for which the sum of over the divisors of is equal to itself.
• The product of any four consecutive numbers is divisible by 24. This is because, among any four consecutive numbers, there must be two even numbers, one of which is a multiple of four, and there must be a multiple of three.
• In 24 dimensions there are 24 even positive definite unimodular lattice
  Unimodular lattice
  In mathematics, a unimodular lattice is a lattice of determinant 1 or −1.The E8 lattice and the Leech lattice are two famous examples.- Definitions :...
  
  s, called the Niemeier lattice
  Niemeier lattice
  In mathematics, a Niemeier lattice is one of the 24positive definite even unimodular lattices of rank 24,which were classified by . gave a simplified proof of the classification. has a sentence mentioning that he found more than 10 such lattices, but gives no further details...
  
  s. One of these is the exceptional Leech lattice
  Leech lattice
  In mathematics, the Leech lattice is an even unimodular lattice Λ24 in 24-dimensional Euclidean space E24 found by .-History:Many of the cross-sections of the Leech lattice, including the Coxeter–Todd lattice and Barnes–Wall lattice, in 12 and 16 dimensions, were found much earlier than...
  
   which has many surprising properties; due to its existence, the answers to many problems such as the kissing number problem
  Kissing number problem
  In geometry, a kissing number is defined as the number of non-overlapping unit spheres that touch another given unit sphere. For a lattice packing the kissing number is the same for every sphere, but for an arbitrary sphere packing the kissing number may vary from one sphere to another...
  
   and sphere packing
  Sphere packing
  In geometry, a sphere packing is an arrangement of non-overlapping spheres within a containing space. The spheres considered are usually all of identical size, and the space is usually three-dimensional Euclidean space...
  
   are known in 24 dimensions but not in many lower dimensions. The Leech lattice is closely related to the equally nice length-24 binary Golay code
  Binary Golay code
  In mathematics and electronics engineering, a binary Golay code is a type of error-correcting code used in digital communications. The binary Golay code, along with the ternary Golay code, has a particularly deep and interesting connection to the theory of finite sporadic groups in mathematics....
  
   and the Steiner system
  Steiner system
  250px|right|thumbnail|The [[Fano plane]] is an S Steiner triple system. The blocks are the 7 lines, each containing 3 points. Every pair of points belongs to a unique line....
  
   S(5,8,24) and the Mathieu group
  Mathieu group
  In the mathematical field of group theory, the Mathieu groups, named after the French mathematician Émile Léonard Mathieu, are five finite simple groups he discovered and reported in papers in 1861 and 1873; these were the first sporadic simple groups discovered...
  
   M₂₄. One construction of the Leech lattice
  Leech lattice
  In mathematics, the Leech lattice is an even unimodular lattice Λ24 in 24-dimensional Euclidean space E24 found by .-History:Many of the cross-sections of the Leech lattice, including the Coxeter–Todd lattice and Barnes–Wall lattice, in 12 and 16 dimensions, were found much earlier than...
  
   is possible because of the remarkable fact that 1²+2²+3²+...+24² =70² is a perfect square
  Square number
  In mathematics, a square number, sometimes also called a perfect square, is an integer that is the square of an integer; in other words, it is the product of some integer with itself...
  
  ; 24 is the only integer greater than 1 with this property. These properties of 24 are related to the fact that the number 24 also appears in several places in the theory of modular form
  Modular form
  In mathematics, a modular form is a analytic function on the upper half-plane satisfying a certain kind of functional equation and growth condition. The theory of modular forms therefore belongs to complex analysis but the main importance of the theory has traditionally been in its connections...
  
  s; for example, the modular discriminant is the 24th power of the Dedekind eta function
  Dedekind eta function
  The Dedekind eta function, named after Richard Dedekind, is a function defined on the upper half-plane of complex numbers, where the imaginary part is positive...
  
  .
• The Barnes-Wall lattice contains 24 lattice
  Lattice (group)
  In mathematics, especially in geometry and group theory, a lattice in Rn is a discrete subgroup of Rn which spans the real vector space Rn. Every lattice in Rn can be generated from a basis for the vector space by forming all linear combinations with integer coefficients...
  
  s.
• The divisors of 24 — namely, {1, 2, 3, 4, 6, 8, 12, 24} — are exactly those n for which every element x of the group of units (Z/nZ)^*
  Multiplicative group of integers modulo n
  In modular arithmetic the set of congruence classes relatively prime to the modulus n form a group under multiplication called the multiplicative group of integers modulo n. It is also called the group of primitive residue classes modulo n. In the theory of rings, a branch of abstract algebra, it...
  
   of the commutative ring
  Commutative ring
  In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
  
   Z/nZ
  Modular arithmetic
  In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
  
   satisfies x² = 1. Thus the multiplicative group (Z/24Z)^* = {±1, ±5, ±7, ±11} is isomorphic
  Group isomorphism
  In abstract algebra, a group isomorphism is a function between two groups that sets up a one-to-one correspondence between the elements of the groups in a way that respects the given group operations. If there exists an isomorphism between two groups, then the groups are called isomorphic...
  
   to the additive group (Z/2Z)³. This fact plays a role in monstrous moonshine
  Monstrous moonshine
  In mathematics, monstrous moonshine, or moonshine theory, is a term devised by John Horton Conway and Simon P. Norton in 1979, used to describe the connection between the monster group M and modular functions .- History :Specifically, Conway and Norton, following an initial observationby John...
  
  .
• The 24-cell, with 24 octahedral cells and 24 vertices, is a self-dual
  Dual polyhedron
  In geometry, polyhedra are associated into pairs called duals, where the vertices of one correspond to the faces of the other. The dual of the dual is the original polyhedron. The dual of a polyhedron with equivalent vertices is one with equivalent faces, and of one with equivalent edges is another...
  
   convex regular 4-polytope
  Convex regular 4-polytope
  In mathematics, a convex regular 4-polytope is a 4-dimensional polytope that is both regular and convex. These are the four-dimensional analogs of the Platonic solids and the regular polygons ....
  
  ; it has no good 3-dimensional analogue.
• For any prime 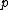greater than 3, is divisible by . Hence, any square of a prime 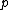expressed in radix 24
  Base 24
  The base- system is a numeral system with 24 as its base.There are 24 hours in a nychthemeron , so solar time includes a base-24 component.See also base 12. Decimal Equivalent...
  
   ends with an 1. For example, 5² = 11₂₄, 7² = 21₂₄, 11² = 51₂₄.
• 24 is the second Granville number, the previous being 6 and the next being 28
  28 (number)
  28 is the natural number following 27 and preceding 29.-In mathematics:It is a composite number, its proper divisors being 1, 2, 4, 7, and 14....
  
  . It is the first Granville number that is not also a conventional perfect number.
• 24 is the largest integer
  Integer
  The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
  
  , which is divisible with no remainder by all natural numbers smaller or equal to its square root.

In science

• The atomic number
  Atomic number
  In chemistry and physics, the atomic number is the number of protons found in the nucleus of an atom and therefore identical to the charge number of the nucleus. It is conventionally represented by the symbol Z. The atomic number uniquely identifies a chemical element...
  
   of chromium
• The number of hours in a day
• 24!
  Factorial
  In mathematics, the factorial of a non-negative integer n, denoted by n!, is the product of all positive integers less than or equal to n...
  
   is an approximation (by 3%) of the Avogadro constant.

In religion

• The number of books in the Tanakh
  Tanakh
  The Tanakh is a name used in Judaism for the canon of the Hebrew Bible. The Tanakh is also known as the Masoretic Text or the Miqra. The name is an acronym formed from the initial Hebrew letters of the Masoretic Text's three traditional subdivisions: The Torah , Nevi'im and Ketuvim —hence...
  
  
• In Christian apocalyptic literature it represents the complete Church, being the sum of the 12 tribes of Israel and the 12 Apostles of the Lamb of God
• Number of Tirthankaras

In music

• There are 24 major and minor keys in Western tonal music, not counting enharmonic
  Enharmonic
  In modern musical notation and tuning, an enharmonic equivalent is a note , interval , or key signature which is equivalent to some other note, interval, or key signature, but "spelled", or named, differently...
  
   equivalents. Therefore, for collections of pieces written in each key, the number of pieces in such a collection; e.g., Chopin
  Frédéric Chopin
  Frédéric François Chopin was a Polish composer and virtuoso pianist. He is considered one of the great masters of Romantic music and has been called "the poet of the piano"....
  
  's 24 Preludes
  Preludes Op. 28 (Chopin)
  Frédéric Chopin wrote a number of preludes for piano solo.-24 Preludes, Op. 28:Chopin's 24 Preludes, Op. 28, are a set of short pieces for the piano, one in each of the twenty-four keys, originally published in 1839 and dedicated to Joseph Christoph Kessler, a composer of piano studies during...
  
  

In sports

• The number of teams that participated in each FIFA World Cup
  FIFA World Cup
  The FIFA World Cup, often simply the World Cup, is an international association football competition contested by the senior men's national teams of the members of Fédération Internationale de Football Association , the sport's global governing body...
  
   finals tournament between 1982 and 1994. Also the number of teams that will participate in the finals of the FIFA Women's World Cup
  FIFA Women's World Cup
  The FIFA Women's World Cup is an international association football competition contested by the senior women's national teams of the members of Fédération Internationale de Football Association , the sport's global governing body. The championship has been awarded every four years since the...
  
   starting in 2015
  2015 FIFA Women's World Cup
  The 2015 FIFA Women's World Cup will be the seventh FIFA Women's World Cup, the quadrennial international women's football world championship tournament...
  
  .
• Four-and-Twenty
  Four-and-Twenty
  Four-and-Twenty was an American Thoroughbred racehorse. He was red and raced by the Alberta Ranches, Ltd. partnership of Max Bell, Frank McMahon and superstar jockey Johnny Longden and his son, Vance. He was sired by a son of the two-time Leading sire in North America, Princequillo...
  
   was an American racehorse.
• Under the basketball
  Basketball
  Basketball is a team sport in which two teams of five players try to score points by throwing or "shooting" a ball through the top of a basketball hoop while following a set of rules...
  
   rules of FIBA
  International Basketball Federation
  The International Basketball Federation, more commonly known as FIBA , from its French name Fédération Internationale de Basketball, is an association of national organizations which governs international competition in basketball...
  
  , the NBA
  National Basketball Association
  The National Basketball Association is the pre-eminent men's professional basketball league in North America. It consists of thirty franchised member clubs, of which twenty-nine are located in the United States and one in Canada...
  
  , and the WNBA
  Women's National Basketball Association
  The Women's National Basketball Association is a women's professional basketball league in the United States. It currently is composed of twelve teams. The league was founded on April 24, 1996 as the women's counterpart to the National Basketball Association...
  
  , the offensive team has 24 seconds
  Shot clock
  A shot clock is used in some sports to quicken the pace of the game. It is normally associated with basketball, but has also found use in sports such as snooker, professional lacrosse, water polo, and korfball....
  
   to attempt a shot.
• The jersey number
  Squad number
  In team sports, the squad number, shirt number, jersey number, sweater number, uniform number or simply a number is the number worn on a player's uniform, to identify and distinguish each player from others wearing the same or similar uniforms...
  
   24 has been retired by several North American sports teams in honor of past playing greats or other key figures:
  • In Major League Baseball
    Major League Baseball
    Major League Baseball is the highest level of professional baseball in the United States and Canada, consisting of teams that play in the National League and the American League...
    
    :
    • The Cincinnati Reds
      Cincinnati Reds
      The Cincinnati Reds are a Major League Baseball team based in Cincinnati, Ohio. They are members of the National League Central Division. The club was established in 1882 as a charter member of the American Association and joined the National League in 1890....
      
      , for Hall of Famer
      National Baseball Hall of Fame and Museum
      The National Baseball Hall of Fame and Museum is an American history museum and hall of fame, located at 25 Main Street in Cooperstown, New York, operated by private interests serving as the central point for the study of the history of baseball in the United States and beyond, the display of...
      
       Tony Pérez
      Tony Pérez
      Atanasio Pérez Rigal , more commonly known as Tony Pérez, is a former Major League Baseball player. He was also known by the nickname "Big Dog," "Big Doggie," and "Doggie."...
      
      .
    • The Los Angeles Dodgers
      Los Angeles Dodgers
      The Los Angeles Dodgers are a professional baseball team based in Los Angeles, California. The Dodgers are members of Major League Baseball's National League West Division. Established in 1883, the team originated in Brooklyn, New York, where it was known by a number of nicknames before becoming...
      
      , for Hall of Fame manager
      Manager (baseball)
      In baseball, the field manager is an individual who is responsible for matters of team strategy on the field and team leadership. Managers are typically assisted by between one and six assistant coaches, whose responsibilities are specialized...
      
       Walter Alston
      Walter Alston
      Walter Emmons Alston , nicknamed "Smokey," was an American baseball player and manager. He was born in Venice, Ohio but grew up in Darrtown. He is a graduate of Miami University in Oxford, Ohio, where he lettered three years in both basketball and baseball and is a member of the University's Hall...
      
      .
    • The St. Louis Cardinals
      St. Louis Cardinals
      The St. Louis Cardinals are a professional baseball team based in St. Louis, Missouri. They are members of the Central Division in the National League of Major League Baseball. The Cardinals have won eleven World Series championships, the most of any National League team, and second overall only to...
      
      , for Hall of Fame manager Whitey Herzog
      Whitey Herzog
      Dorrel Norman Elvert "Whitey" Herzog is a former Major League Baseball manager. Born in New Athens, Illinois, he made his debut as a player in 1956 with the Washington Senators. After his playing career ended in 1963, Herzog went on to perform a variety of roles in Major League Baseball, including...
      
      .
    • The San Francisco Giants
      San Francisco Giants
      The San Francisco Giants are a Major League Baseball team based in San Francisco, California, playing in the National League West Division....
      
      , for Hall of Famer Willie Mays
      Willie Mays
      Willie Howard Mays, Jr. is a retired American professional baseball player who played the majority of his major league career with the New York and San Francisco Giants before finishing with the New York Mets. Nicknamed The Say Hey Kid, Mays was elected to the Baseball Hall of Fame in 1979, his...
      
      .
    • The Seattle Mariners
      Seattle Mariners
      The Seattle Mariners are a professional baseball team based in Seattle, Washington. Enfranchised in , the Mariners are a member of the Western Division of Major League Baseball's American League. Safeco Field has been the Mariners' home ballpark since July...
      
       have yet to retire any numbers, but took #24 out of circulation when Ken Griffey, Jr.
      Ken Griffey, Jr.
      George Kenneth "Ken" Griffey, Jr. , nicknamed "Junior" and "The Kid", is a former Major League Baseball outfielder and during his final years, designated hitter...
      
       was traded from the team after the 1999 season. The number was reissued to Griffey when he rejoined the team in 2009, and taken out of circulation again after his retirement during the 2010 season.
  • In the NBA
    National Basketball Association
    The National Basketball Association is the pre-eminent men's professional basketball league in North America. It consists of thirty franchised member clubs, of which twenty-nine are located in the United States and one in Canada...
    
    :
    • The Boston Celtics
      Boston Celtics
      The Boston Celtics are a National Basketball Association team based in Boston, Massachusetts. They play in the Atlantic Division of the Eastern Conference. Founded in 1946, the team is currently owned by Boston Basketball Partners LLC. The Celtics play their home games at the TD Garden, which...
      
      , for Hall of Famer Sam Jones
      Sam Jones (basketball)
      Samuel Jones is a retired American professional basketball player at shooting guard and a member of the Naismith Memorial Basketball Hall of Fame. He was known for his quickness and game-winning shots, especially during the NBA Playoffs...
      
      .
    • The Golden State Warriors
      Golden State Warriors
      The Golden State Warriors are an American professional basketball team based in Oakland, California. They are part of the Pacific Division of the Western Conference in the National Basketball Association...
      
      , for Hall of Famer Rick Barry
      Rick Barry
      Richard Francis Dennis Barry III , better known as Rick Barry, is a retired American professional basketball player. He is considered by many veteran basketball observers to be one of the greatest pure small forwards of all time as a result of his very precise outside shot, uncanny court vision,...
      
      .
    • The Houston Rockets
      Houston Rockets
      The Houston Rockets are an American professional basketball team based in Houston, Texas. The team plays in the Southwest Division of the Western Conference in the National Basketball Association . The team was established in 1967, and played in San Diego, California for four years, before being...
      
      , for Hall of Famer Moses Malone
      Moses Malone
      Moses Eugene Malone is a retired American Hall of Fame basketball player who starred in both the American Basketball Association and the National Basketball Association...
      
      .
    • The New York Knicks
      New York Knicks
      The New York Knickerbockers, prominently known as the Knicks, are a professional basketball team based in New York City. They are part of the Atlantic Division of the Eastern Conference in the National Basketball Association...
      
      , for Hall of Famer Bill Bradley
      Bill Bradley
      William Warren "Bill" Bradley is an American hall of fame basketball player, Rhodes scholar, and former three-term Democratic U.S. Senator from New Jersey. He ran unsuccessfully for the Democratic Party's nomination for President in the 2000 election.Bradley was born and raised in a suburb of St....
      
      .
    • The Philadelphia 76ers
      Philadelphia 76ers
      The Philadelphia 76ers are a professional basketball team based in Philadelphia, Pennsylvania. They play in the Atlantic Division of the Eastern Conference of the National Basketball Association . Originally known as the Syracuse Nationals, they are one of the oldest franchises in the NBA...
      
      , for Bobby Jones.
    • The Phoenix Suns
      Phoenix Suns
      The Phoenix Suns are a professional basketball team based in Phoenix, Arizona. They are members of the Pacific Division of the Western Conference in the National Basketball Association and the only team in their division not to be based in California. Their home arena since 1992 has been the US...
      
      , for Tom Chambers.
    • The Seattle SuperSonics
      Seattle SuperSonics
      The Seattle SuperSonics were an American professional basketball team based in Seattle, Washington that played in the Pacific and Northwest Divisions of the National Basketball Association from 1967 until 2008. Following the 2007–08 season, the team relocated to Oklahoma City, and now plays as...
      
      , for Spencer Haywood
      Spencer Haywood
      Spencer Haywood is a retired American professional basketball player.- High school :In 1964, Haywood moved to Detroit, Michigan, where he attended Pershing High School...
      
      . The team has since relocated
      Seattle SuperSonics relocation to Oklahoma City
      The Seattle SuperSonics relocation to Oklahoma City was a successful effort by the ownership group of the Seattle SuperSonics to move the team to Oklahoma City...
      
       to become the Oklahoma City Thunder
      Oklahoma City Thunder
      The Oklahoma City Thunder are a professional basketball franchise based in Oklahoma City, Oklahoma. They play in the Northwest Division of the Western Conference in the National Basketball Association ; their home court is at Chesapeake Energy Arena....
      
      , but the Thunder has yet to issue any of the numbers retired by the franchise in Seattle.
    • The Los Angeles Lakers
      Los Angeles Lakers
      The Los Angeles Lakers are an American professional basketball team based in Los Angeles, California. They play in the Pacific Division of the Western Conference in the National Basketball Association...
      
      , for Kobe Bryant
      Kobe Bryant
      Kobe Bean Bryant is an American professional basketball player who plays shooting guard for the Los Angeles Lakers of the National Basketball Association . Bryant enjoyed a successful high school basketball career at Lower Merion High School, where he was recognized as the top high school...
      
      .
  • In the NHL
    National Hockey League
    The National Hockey League is an unincorporated not-for-profit association which operates a major professional ice hockey league of 30 franchised member clubs, of which 7 are currently located in Canada and 23 in the United States...
    
    :
    • The Boston Bruins
      Boston Bruins
      The Boston Bruins are a professional ice hockey team based in Boston, Massachusetts, USA. They are members of the Northeast Division of the Eastern Conference of the National Hockey League . The team has been in existence since 1924, and is the league's third-oldest team and its oldest in the...
      
      , for Terry O'Reilly
      Terry O'Reilly
      Terence Joseph James O'Reilly is a retired ice hockey right winger, who played for the NHL's Boston Bruins, and one of the most effective enforcers in NHL history....
      
      .
    • The St. Louis Blues
      St. Louis Blues
      The St. Louis Blues are a professional ice hockey team based in St. Louis, Missouri. They are members of the Central Division of the Western Conference of the National Hockey League . The team is named after the famous W. C. Handy song "St. Louis Blues", and plays in the 19,150-seat Scottrade...
      
      , for Hall of Famer
      Hockey Hall of Fame
      The Hockey Hall of Fame is located in Toronto, Ontario, Canada. Dedicated to the history of ice hockey, it is both a museum and a hall of fame. It holds exhibits about players, teams, National Hockey League records, memorabilia and NHL trophies, including the Stanley Cup...
      
       Bernie Federko
      Bernie Federko
      Bernard Allan Federko is a retired professional ice hockey centre who played fourteen seasons in the National Hockey League from 1976 through 1990.-Playing career:...
      
      .
  • In the NFL
    National Football League
    The National Football League is the highest level of professional American football in the United States, and is considered the top professional American football league in the world. It was formed by eleven teams in 1920 as the American Professional Football Association, with the league changing...
    
    :
    • The Baltimore Colts, for Hall of Famer
      Pro Football Hall of Fame
      The Pro Football Hall of Fame is the hall of fame of professional football in the United States with an emphasis on the National Football League . It opened in Canton, Ohio, on September 7, 1963, with 17 charter inductees...
      
       Lenny Moore
      Lenny Moore
      Leonard Edward Moore is a former American football halfback who played for Penn State in college and the Baltimore Colts. He came to the Colts in 1956, and had a productive first pro season and was named the NFL Rookie of The Year...
      
      . The current Indianapolis Colts
      Indianapolis Colts
      The Indianapolis Colts are a professional American football team based in Indianapolis. They are currently members of the South Division of the American Football Conference in the National Football League ....
      
       have yet to retire any numbers, but continue to honor all numbers retired by the franchise in Baltimore.
• The number of accepted runners in the Melbourne Cup
  Melbourne Cup
  The Melbourne Cup is Australia's major Thoroughbred horse race. Marketed as "the race that stops a nation", it is a 3,200 metre race for three-year-olds and over. It is the richest "two-mile" handicap in the world, and one of the richest turf races...
  
  
• The number of a car in the NASCAR Sprint Cup Series owned by Hendrick Motorsports
  Hendrick Motorsports
  Hendrick Motorsports , originally named All Star Racing, is a current American auto racing team created in 1984 by Rick Hendrick. The team currently competes in the NASCAR Sprint Cup Series with Chevrolet Impalas...
  
  . The car has been driven by Jeff Gordon
  Jeff Gordon
  Jeffery Michael "Jeff" Gordon is a professional NASCAR driver. He is the driver of the #24 Drive to End Hunger/DuPont/Pepsi Chevrolet Impala. He is a four-time Sprint Cup Series champion and a three-time Daytona 500 winner. He is third on the all-time wins list, with 85 career wins, and has the...
  
   since its introduction in 1992.

In other fields

• The number of bit
  Bit
  A bit is the basic unit of information in computing and telecommunications; it is the amount of information stored by a digital device or other physical system that exists in one of two possible distinct states...
  
  s a computer needs to represent TrueColor images (for a maximum of 16,777,216 colours). (But greater numbers of bits provide more accurate colors. "TrueColor" is one of many possible representations of colors.)
• The number of carat
  Carat (purity)
  The karat or carat is a unit of purity for gold alloys.- Measure :Karat purity is measured as 24 times the purity by mass:where...
  
  s representing 100% pure gold.
• The number of cycles in the Chinese solar year
  Chinese calendar
  The Chinese calendar is a lunisolar calendar, incorporating elements of a lunar calendar with those of a solar calendar. It is not exclusive to China, but followed by many other Asian cultures as well...
  
  .
• The number of frames per second at which motion picture film is usually projected.
• The number of hours in a day.
• The number of letters in both the modern and classical Greek alphabet
  Greek alphabet
  The Greek alphabet is the script that has been used to write the Greek language since at least 730 BC . The alphabet in its classical and modern form consists of 24 letters ordered in sequence from alpha to omega...
  
  . For the latter reason, also the number of chapters or "books" into which Homer
  Homer
  In the Western classical tradition Homer , is the author of the Iliad and the Odyssey, and is revered as the greatest ancient Greek epic poet. These epics lie at the beginning of the Western canon of literature, and have had an enormous influence on the history of literature.When he lived is...
  
  's Odyssey
  Odyssey
  The Odyssey is one of two major ancient Greek epic poems attributed to Homer. It is, in part, a sequel to the Iliad, the other work ascribed to Homer. The poem is fundamental to the modern Western canon, and is the second—the Iliad being the first—extant work of Western literature...
  
  and Iliad
  Iliad
  The Iliad is an epic poem in dactylic hexameters, traditionally attributed to Homer. Set during the Trojan War, the ten-year siege of the city of Troy by a coalition of Greek states, it tells of the battles and events during the weeks of a quarrel between King Agamemnon and the warrior Achilles...
  
  came to be divided.
• 24
  24 (TV series)
  24 is an American television series produced for the Fox Network and syndicated worldwide, starring Kiefer Sutherland as Counter Terrorist Unit agent Jack Bauer. Each 24-episode season covers 24 hours in the life of Bauer, using the real time method of narration...
  
  , television series starring Kiefer Sutherland
  Kiefer Sutherland
  Kiefer Sutherland is an English-born Canadian actor, producer and director, best known for his portrayal of Jack Bauer on the Fox thriller drama series 24 for which he has won an Emmy Award , a Golden Globe award , two Screen Actors Guild Awards and two Satellite...
  
  . Each episode covers one hour, with 24 episodes making up one entire "day".
• The number of points on a backgammon
  Backgammon
  Backgammon is one of the oldest board games for two players. The playing pieces are moved according to the roll of dice, and players win by removing all of their pieces from the board. There are many variants of backgammon, most of which share common traits...
  
   board.
• When pronounced "two-four", a 24-pack of beer (Canadianism
  Canadian English
  Canadian English is the variety of English spoken in Canada. English is the first language, or "mother tongue", of approximately 24 million Canadians , and more than 28 million are fluent in the language...
  
  ).
• A children's mathematical game involving the use of any of the four standard operations on four numbers on a card to get 24 (see Math 24)
• The maximum number of Knight Companions in the Order of the Garter
  Order of the Garter
  The Most Noble Order of the Garter, founded in 1348, is the highest order of chivalry, or knighthood, existing in England. The order is dedicated to the image and arms of St...
  
  
• 24 is considered an unlucky number in Cantonese culture because its pronunciation is similar to that of "easy to die". For this reason, many buildings skip this floor number. The same goes for 13, 34, 44, etc.
• A Straight Edge
  Straight edge
  Straight edge is a subculture of hardcore punk whose adherents refrain from using alcohol, tobacco, and other recreational drugs. It was a direct reaction to the sexual revolution, hedonism, and excess associated with punk rock. For some, this extends to not engaging in promiscuous sex, following a...
  
   symbol, for X is the 24th letter of the alphabet.
• Slang for ecstasy
• In Brazil
  Brazil
  Brazil , officially the Federative Republic of Brazil , is the largest country in South America. It is the world's fifth largest country, both by geographical area and by population with over 192 million people...
  
  , the number is associated with homosexuals
  Homosexuality
  Homosexuality is romantic or sexual attraction or behavior between members of the same sex or gender. As a sexual orientation, homosexuality refers to "an enduring pattern of or disposition to experience sexual, affectional, or romantic attractions" primarily or exclusively to people of the same...
  
   due to the number representing the deer
  Deer
  Deer are the ruminant mammals forming the family Cervidae. Species in the Cervidae family include white-tailed deer, elk, moose, red deer, reindeer, fallow deer, roe deer and chital. Male deer of all species and female reindeer grow and shed new antlers each year...
  
   in the gambling game Jogo do Bicho
  Jogo do Bicho
  Jogo do Bicho is an illegal gambling game in Brazil, prohibited by federal law since 1946. Very popular throughout the country, the "game" is actually a lottery-type drawing operated on a regional basis by mobsters known as contraventores , bicheiros or banqueiros...
  
   and the word viado (a misspelling of veado, deer in Portuguese
  Portuguese language
  Portuguese is a Romance language that arose in the medieval Kingdom of Galicia, nowadays Galicia and Northern Portugal. The southern part of the Kingdom of Galicia became independent as the County of Portugal in 1095...
  
  ) being a slang for homosexuals.

External links

• My Favorite Numbers: 24, John C. Baez
  John C. Baez
  John Carlos Baez is an American mathematical physicist and a professor of mathematics at the University of California, Riverside in Riverside, California. He is known for his work on spin foams in loop quantum gravity. More recently, his research has focused on applications of higher categories...