Composite number
Encyclopedia
A composite number is a positive integer which has a positive divisor
other than one or itself. In other words a composite number is any positive integer
greater than one that is not a prime number
.
So, if n > 0 is an integer and there are integers 1 < a, b < n such that n = a × b, then n is composite. By definition, every integer greater than one is either a prime number
or a composite number. The number one is a unit
– it is neither prime nor composite. For example, the integer 14 is a composite number because it can be factored as 2 × 7. Likewise, the integers 2 and 3 are not composite numbers because each of them can only be divided by one and itself.
The first 105 composite numbers are
Every composite number can be written as the product of two or more (not necessarily distinct) primes; furthermore, this representation is unique up to the order of the factors. This is called the fundamental theorem of arithmetic
.
Wilson's theorem provides a test for whether a number is prime or composite:
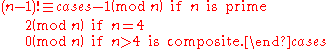
or 2-almost prime (the factors need not be distinct, hence squares of primes are included). A composite number with three distinct prime factors is a sphenic number
. In some applications, it is necessary to differentiate between composite numbers with an odd number of distinct prime factors and those with an even number of distinct prime factors. For the latter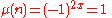
(where μ is the Möbius function
and x is half the total of prime factors), while for the former
Note however that for prime numbers the function also returns -1, and that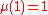
. For a number n with one or more repeated prime factors, 
.
If all the prime factors of a number are repeated it is called a powerful number
. If none of its prime factors are repeated, it is called squarefree
. (All prime numbers and 1 are squarefree.)
Another way to classify composite numbers is by counting the number of divisors. All composite numbers have at least three divisors. In the case of squares of primes, those divisors are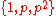
. A number n that has more divisors than any x < n is a highly composite number
(though the first two such numbers are 1 and 2).
Divisor
In mathematics, a divisor of an integer n, also called a factor of n, is an integer which divides n without leaving a remainder.-Explanation:...
other than one or itself. In other words a composite number is any positive integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
greater than one that is not a prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
.
So, if n > 0 is an integer and there are integers 1 < a, b < n such that n = a × b, then n is composite. By definition, every integer greater than one is either a prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
or a composite number. The number one is a unit
Unit (ring theory)
In mathematics, an invertible element or a unit in a ring R refers to any element u that has an inverse element in the multiplicative monoid of R, i.e. such element v that...
– it is neither prime nor composite. For example, the integer 14 is a composite number because it can be factored as 2 × 7. Likewise, the integers 2 and 3 are not composite numbers because each of them can only be divided by one and itself.
The first 105 composite numbers are
- 4, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21, 22, 24, 25, 26, 27, 28, 30, 32, 33, 34, 35, 36, 38, 39, 40, 42, 44, 45, 46, 48, 49, 50, 51, 52, 54, 55, 56, 57, 58, 60, 62, 63, 64, 65, 66, 68, 69, 70, 72, 74, 75, 76, 77, 78, 80, 81, 82, 84, 85, 86, 87, 88, 90, 91, 92, 93, 94, 95, 96, 98, 99, 100, 102, 104, 105, 106, 108, 110, 111, 112, 114, 115, 116, 117, 118, 119, 120, 121, 122, 123, 124, 125, 126, 128, 129, 130, 132, 133, 134, 135, 136, 138, 140.
Every composite number can be written as the product of two or more (not necessarily distinct) primes; furthermore, this representation is unique up to the order of the factors. This is called the fundamental theorem of arithmetic
Fundamental theorem of arithmetic
In number theory, the fundamental theorem of arithmetic states that any integer greater than 1 can be written as a unique product of prime numbers...
.
Wilson's theorem provides a test for whether a number is prime or composite:
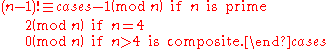
Types of composite numbers
One way to classify composite numbers is by counting the number of prime factors. A composite number with two prime factors is a semiprimeSemiprime
In mathematics, a semiprime is a natural number that is the product of two prime numbers. The first few semiprimes are 4, 6, 9, 10, 14, 15, 21, 22, 25, 26, ... ....
or 2-almost prime (the factors need not be distinct, hence squares of primes are included). A composite number with three distinct prime factors is a sphenic number
Sphenic number
In number theory, a sphenic number is a positive integer which is the product of three distinct prime numbers.Note that this definition is more stringent than simply requiring the integer to have exactly three prime factors; e.g. 60 = 22 × 3 × 5 has exactly 3 prime factors, but is not sphenic.All...
. In some applications, it is necessary to differentiate between composite numbers with an odd number of distinct prime factors and those with an even number of distinct prime factors. For the latter
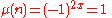
(where μ is the Möbius function
Möbius function
The classical Möbius function μ is an important multiplicative function in number theory and combinatorics. The German mathematician August Ferdinand Möbius introduced it in 1832...
and x is half the total of prime factors), while for the former
Note however that for prime numbers the function also returns -1, and that
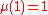. For a number n with one or more repeated prime factors, .If all the prime factors of a number are repeated it is called a powerful number
Powerful number
A powerful number is a positive integer m such that for every prime number p dividing m, p2 also divides m. Equivalently, a powerful number is the product of a square and a cube, that is, a number m of the form m = a2b3, where a and b are positive integers. Powerful numbers are also known as...
. If none of its prime factors are repeated, it is called squarefree
Square-free integer
In mathematics, a square-free, or quadratfrei, integer is one divisible by no perfect square, except 1. For example, 10 is square-free but 18 is not, as it is divisible by 9 = 32...
. (All prime numbers and 1 are squarefree.)
Another way to classify composite numbers is by counting the number of divisors. All composite numbers have at least three divisors. In the case of squares of primes, those divisors are
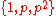. A number n that has more divisors than any x < n is a highly composite numberHighly composite number
A highly composite number is a positive integer with more divisors than any positive integer smaller than itself.The initial or smallest twenty-one highly composite numbers are listed in the table at right....
(though the first two such numbers are 1 and 2).