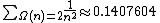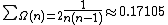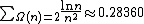Semiprime
Encyclopedia
In mathematics
, a semiprime (also called biprime or 2-almost prime, or pq number) is a natural number
that is the product of two (not necessarily distinct) prime number
s. The first few semiprimes are 4, 6, 9, 10, 14, 15, 21, 22, 25, 26, ... .
, the largest known semiprime is (243,112,609 − 1)2, which has over 25 million digits. This is the square of the largest known prime
. The square of any prime number is a semiprime, so the largest known semiprime will always be the square of the largest known prime, unless the factors of the semiprime are not known. It is conceivable that a way could be found to prove a larger number is a semiprime without knowing the two factors, but so far only the previous has happened for smaller semiprimes.
If otherwise p and q are the same,
and number theory
, most notably in public key cryptography, where they are used by RSA and pseudorandom number generator
s such as Blum Blum Shub. These methods rely on the fact that finding two large primes and multiplying them together is computationally simple, whereas finding the original factors
appears to be difficult. In the RSA Factoring Challenge
, RSA Security
offered prizes for the factoring of specific large semiprimes and several prizes were awarded. The most recent such challenge closed in 2007.
In practical cryptography, it is not sufficient to choose just any semiprime; a good number must evade a number of well-known special-purpose algorithms that can factor numbers of certain form. The factors p and q of n should both be very large, around the same order of magnitude as the square root of n; this makes trial division
and Pollard's rho algorithm
impractical. At the same time they should not be too close together, or else the number can be quickly factored by Fermat's factorization method
. The number may also be chosen so that none of p − 1, p + 1, q − 1, or q + 1 are smooth number
s, protecting against Pollard's p − 1 algorithm or Williams' p + 1 algorithm. However, these checks cannot take future algorithms or secret algorithms into account, introducing the possibility that numbers in use today may be broken by special-purpose algorithms.
In 1974 the Arecibo message
was sent with a radio signal aimed at a star cluster
. It consisted of 1679 binary digits intended to be interpreted as a 23×73 bitmap
image. The number 1679 = 23×73 was chosen because it is a semiprime and therefore can only be broken down into 23 rows and 73 columns, or 73 rows and 23 columns.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a semiprime (also called biprime or 2-almost prime, or pq number) is a natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
that is the product of two (not necessarily distinct) prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
s. The first few semiprimes are 4, 6, 9, 10, 14, 15, 21, 22, 25, 26, ... .
, the largest known semiprime is (243,112,609 − 1)2, which has over 25 million digits. This is the square of the largest known prime
Largest known prime
The largest known prime number is the largest integer that is currently known to be a prime number.It was proven by Euclid that there are infinitely many prime numbers; thus, there is always a prime greater than the largest known prime. Many mathematicians and hobbyists search for large prime numbers...
. The square of any prime number is a semiprime, so the largest known semiprime will always be the square of the largest known prime, unless the factors of the semiprime are not known. It is conceivable that a way could be found to prove a larger number is a semiprime without knowing the two factors, but so far only the previous has happened for smaller semiprimes.
Properties
- A semiprime is either a squareSquare numberIn mathematics, a square number, sometimes also called a perfect square, is an integer that is the square of an integer; in other words, it is the product of some integer with itself...
of a prime or square-freeSquare-free integerIn mathematics, a square-free, or quadratfrei, integer is one divisible by no perfect square, except 1. For example, 10 is square-free but 18 is not, as it is divisible by 9 = 32...
.
- The value of Euler's totient functionEuler's totient functionIn number theory, the totient \varphi of a positive integer n is defined to be the number of positive integers less than or equal to n that are coprime to n In number theory, the totient \varphi(n) of a positive integer n is defined to be the number of positive integers less than or equal to n that...
for a semiprime n = pq is particularly simple when p and q are distinct:
-
- φ(n) = (p − 1) (q − 1) = p q − (p + q) + 1 = n − (p + q) + 1.
If otherwise p and q are the same,
-
- φ(n) = φ(p2) = (p − 1) p = p2 − p = n − p.
- The total number of prime factorPrime factorIn number theory, the prime factors of a positive integer are the prime numbers that divide that integer exactly, without leaving a remainder. The process of finding these numbers is called integer factorization, or prime factorization. A prime factor can be visualized by understanding Euclid's...
s for a semiprime is by definition
-
-
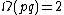 .
.
-
- The concept of the prime zeta function can be adopted to semiprimes, which defines constants like
Applications
Semiprimes are highly useful in the area of cryptographyCryptography
Cryptography is the practice and study of techniques for secure communication in the presence of third parties...
and number theory
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, most notably in public key cryptography, where they are used by RSA and pseudorandom number generator
Pseudorandom number generator
A pseudorandom number generator , also known as a deterministic random bit generator , is an algorithm for generating a sequence of numbers that approximates the properties of random numbers...
s such as Blum Blum Shub. These methods rely on the fact that finding two large primes and multiplying them together is computationally simple, whereas finding the original factors
Integer factorization
In number theory, integer factorization or prime factorization is the decomposition of a composite number into smaller non-trivial divisors, which when multiplied together equal the original integer....
appears to be difficult. In the RSA Factoring Challenge
RSA Factoring Challenge
The RSA Factoring Challenge was a challenge put forward by RSA Laboratories on March 18, 1991 to encourage research into computational number theory and the practical difficulty of factoring large integers and cracking RSA keys used in cryptography...
, RSA Security
RSA Security
RSA, the security division of EMC Corporation, is headquartered in Bedford, Massachusetts, United States, and maintains offices in Australia, Ireland, Israel, the United Kingdom, Singapore, India, China, Hong Kong and Japan....
offered prizes for the factoring of specific large semiprimes and several prizes were awarded. The most recent such challenge closed in 2007.
In practical cryptography, it is not sufficient to choose just any semiprime; a good number must evade a number of well-known special-purpose algorithms that can factor numbers of certain form. The factors p and q of n should both be very large, around the same order of magnitude as the square root of n; this makes trial division
Trial division
Trial division is the most laborious but easiest to understand of the integer factorization algorithms. Its ease of implementation makes it a viable integer factorization option for devices with little available memory, such as graphing calculators....
and Pollard's rho algorithm
Pollard's rho algorithm
Pollard's rho algorithm is a special-purpose integer factorization algorithm. It was invented by John Pollard in 1975. It is particularly effective at splitting composite numbers with small factors.-Core ideas:...
impractical. At the same time they should not be too close together, or else the number can be quickly factored by Fermat's factorization method
Fermat's factorization method
Fermat's factorization method, named after Pierre de Fermat, is based on the representation of an odd integer as the difference of two squares:N = a^2 - b^2.\...
. The number may also be chosen so that none of p − 1, p + 1, q − 1, or q + 1 are smooth number
Smooth number
In number theory, a smooth number is an integer which factors completely into small prime numbers. The term seems to have been coined by Leonard Adleman. Smooth numbers are especially important in cryptography relying on factorization.-Definition:...
s, protecting against Pollard's p − 1 algorithm or Williams' p + 1 algorithm. However, these checks cannot take future algorithms or secret algorithms into account, introducing the possibility that numbers in use today may be broken by special-purpose algorithms.
In 1974 the Arecibo message
Arecibo message
The Arecibo message was broadcast into space a single time via frequency modulated radio waves at a ceremony to mark the remodeling of the Arecibo radio telescope on 16 November 1974. It was aimed at the globular star cluster M13 some 25,000 light years away because M13 was a large and close...
was sent with a radio signal aimed at a star cluster
Star cluster
Star clusters or star clouds are groups of stars. Two types of star clusters can be distinguished: globular clusters are tight groups of hundreds of thousands of very old stars which are gravitationally bound, while open clusters, more loosely clustered groups of stars, generally contain less than...
. It consisted of 1679 binary digits intended to be interpreted as a 23×73 bitmap
Bitmap
In computer graphics, a bitmap or pixmap is a type of memory organization or image file format used to store digital images. The term bitmap comes from the computer programming terminology, meaning just a map of bits, a spatially mapped array of bits. Now, along with pixmap, it commonly refers to...
image. The number 1679 = 23×73 was chosen because it is a semiprime and therefore can only be broken down into 23 rows and 73 columns, or 73 rows and 23 columns.