Granville number
Encyclopedia
In mathematics
, specifically number theory
, Granville numbers are an extension of the perfect number
s.
proposed the following construction of the set
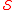 :
:
A Granville number is an element of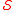 for which strict equality holds i.e. it is equal to the sum of its proper divisors that are also in
for which strict equality holds i.e. it is equal to the sum of its proper divisors that are also in 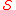 . Granville numbers are also called
. Granville numbers are also called 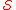 -perfect numbers.
-perfect numbers.
 can be -deficient, -perfect, or -abundant. In particular, 2-perfect numbers
can be -deficient, -perfect, or -abundant. In particular, 2-perfect numbers
are a proper subset of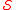 .
.
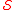 -deficient numbers. That is, the
-deficient numbers. That is, the 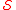 -deficient numbers are the natural numbers that are strictly less than the sum of their divisors in
-deficient numbers are the natural numbers that are strictly less than the sum of their divisors in 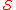 .
.
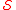 -perfect numbers. That is, the
-perfect numbers. That is, the  -perfect numbers are the natural numbers that are equal the sum of their divisors in
-perfect numbers are the natural numbers that are equal the sum of their divisors in 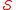 . The first few
. The first few 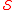 -perfect numbers are:
-perfect numbers are:
Every perfect number
is also -perfect. However, there are numbers such as 24 which are
-perfect. However, there are numbers such as 24 which are 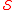 -perfect but not perfect. The only known
-perfect but not perfect. The only known  -perfect number with three distinct prime factors is 126 = 2 · 3² · 7 .
-perfect number with three distinct prime factors is 126 = 2 · 3² · 7 .
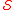 -abundant numbers. That is, the
-abundant numbers. That is, the 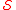 -abundant numbers are the natural numbers that are strictly greater than the sum of their divisors in
-abundant numbers are the natural numbers that are strictly greater than the sum of their divisors in 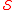 ; they belong to the complement
; they belong to the complement
of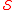 . The first few
. The first few 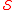 -abundant numbers are:
-abundant numbers are:
and every perfect number
is in because the restriction of the divisors sum to members of
because the restriction of the divisors sum to members of  either decreases the divisors sum or leaves it unchanged. The first natural number that is not in
either decreases the divisors sum or leaves it unchanged. The first natural number that is not in  is the smallest abundant number, which is 12. The next two abundant numbers, 18 and 20, are also not in
is the smallest abundant number, which is 12. The next two abundant numbers, 18 and 20, are also not in  . However, the fourth abundant number, 24, is in
. However, the fourth abundant number, 24, is in  because the sum of its proper divisors in
because the sum of its proper divisors in  is:
is:
In other words, 24 is abundant but not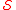 -abundant because 12 is not in
-abundant because 12 is not in 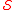 . In fact, 24 is
. In fact, 24 is  -perfect - it is the smallest number that is
-perfect - it is the smallest number that is 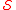 -perfect but not perfect.
-perfect but not perfect.
The smallest odd abundant number that is in is 2835, and the smallest pair of consecutive numbers that are not in
is 2835, and the smallest pair of consecutive numbers that are not in 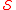 are 5984 and 5985.
are 5984 and 5985.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, specifically number theory
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, Granville numbers are an extension of the perfect number
Perfect number
In number theory, a perfect number is a positive integer that is equal to the sum of its proper positive divisors, that is, the sum of its positive divisors excluding the number itself . Equivalently, a perfect number is a number that is half the sum of all of its positive divisors i.e...
s.
The Granville set
In 1996, Andrew GranvilleAndrew Granville
Andrew James Granville is a British mathematician, working in the field of number theory.He has been a faculty member at the Université de Montréal since 2002. Before moving to Montreal he was a mathematics professor at University of Georgia from 1991 until 2002...
proposed the following construction of the set
Set
A set is a collection of well defined and distinct objects, considered as an object in its own right. Sets are one of the most fundamental concepts in mathematics. Developed at the end of the 19th century, set theory is now a ubiquitous part of mathematics, and can be used as a foundation from...
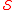 :
:- Let
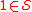 and for all
and for all  let
let  if:
if:
A Granville number is an element of
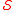 for which strict equality holds i.e. it is equal to the sum of its proper divisors that are also in
for which strict equality holds i.e. it is equal to the sum of its proper divisors that are also in 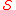 . Granville numbers are also called
. Granville numbers are also called 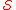 -perfect numbers.
-perfect numbers.General properties
The elements of can be -deficient, -perfect, or -abundant. In particular, 2-perfect numbers
can be -deficient, -perfect, or -abundant. In particular, 2-perfect numbersPerfect number
In number theory, a perfect number is a positive integer that is equal to the sum of its proper positive divisors, that is, the sum of its positive divisors excluding the number itself . Equivalently, a perfect number is a number that is half the sum of all of its positive divisors i.e...
are a proper subset of
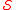 .
.S-deficient numbers
Numbers that fulfill the strict form of the inequality in the above definition are known as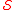 -deficient numbers. That is, the
-deficient numbers. That is, the 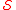 -deficient numbers are the natural numbers that are strictly less than the sum of their divisors in
-deficient numbers are the natural numbers that are strictly less than the sum of their divisors in 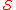 .
.S-perfect numbers
Numbers that fulfill equality in the above definition are known as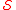 -perfect numbers. That is, the
-perfect numbers. That is, the  -perfect numbers are the natural numbers that are equal the sum of their divisors in
-perfect numbers are the natural numbers that are equal the sum of their divisors in 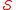 . The first few
. The first few 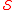 -perfect numbers are:
-perfect numbers are:- 6, 24, 28, 96, 126, 224, 384, 496, 1536, 1792, 6144, 8128, 14336, ...
Every perfect number
Perfect number
In number theory, a perfect number is a positive integer that is equal to the sum of its proper positive divisors, that is, the sum of its positive divisors excluding the number itself . Equivalently, a perfect number is a number that is half the sum of all of its positive divisors i.e...
is also
 -perfect. However, there are numbers such as 24 which are
-perfect. However, there are numbers such as 24 which are 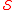 -perfect but not perfect. The only known
-perfect but not perfect. The only known  -perfect number with three distinct prime factors is 126 = 2 · 3² · 7 .
-perfect number with three distinct prime factors is 126 = 2 · 3² · 7 .S-abundant numbers
Numbers that violate the inequality in the above definition are known as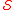 -abundant numbers. That is, the
-abundant numbers. That is, the 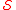 -abundant numbers are the natural numbers that are strictly greater than the sum of their divisors in
-abundant numbers are the natural numbers that are strictly greater than the sum of their divisors in 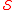 ; they belong to the complement
; they belong to the complementComplement (set theory)
In set theory, a complement of a set A refers to things not in , A. The relative complement of A with respect to a set B, is the set of elements in B but not in A...
of
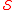 . The first few
. The first few 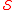 -abundant numbers are:
-abundant numbers are:- 12, 18, 20, 30, 42, 48, 56, 66, 70, 72, 78, 80, 84, 88, 90, 102, 104, ...
Examples
Every deficient numberDeficient number
In number theory, a deficient number or defective number is a number n for which the sum of divisors σIn number theory, a deficient number or defective number is a number n for which the sum of divisors σIn number theory, a deficient number or defective number is a number n for which...
and every perfect number
Perfect number
In number theory, a perfect number is a positive integer that is equal to the sum of its proper positive divisors, that is, the sum of its positive divisors excluding the number itself . Equivalently, a perfect number is a number that is half the sum of all of its positive divisors i.e...
is in
 because the restriction of the divisors sum to members of
because the restriction of the divisors sum to members of  either decreases the divisors sum or leaves it unchanged. The first natural number that is not in
either decreases the divisors sum or leaves it unchanged. The first natural number that is not in  is the smallest abundant number, which is 12. The next two abundant numbers, 18 and 20, are also not in
is the smallest abundant number, which is 12. The next two abundant numbers, 18 and 20, are also not in  . However, the fourth abundant number, 24, is in
. However, the fourth abundant number, 24, is in  because the sum of its proper divisors in
because the sum of its proper divisors in  is:
is:- 1 + 2 + 3 + 4 + 6 + 8 = 24
In other words, 24 is abundant but not
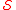 -abundant because 12 is not in
-abundant because 12 is not in 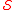 . In fact, 24 is
. In fact, 24 is  -perfect - it is the smallest number that is
-perfect - it is the smallest number that is 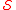 -perfect but not perfect.
-perfect but not perfect.The smallest odd abundant number that is in
 is 2835, and the smallest pair of consecutive numbers that are not in
is 2835, and the smallest pair of consecutive numbers that are not in 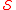 are 5984 and 5985.
are 5984 and 5985.