Kervaire invariant
Encyclopedia
In mathematics, the Kervaire invariant, named for Michel Kervaire
, is defined in geometric topology
. It is an invariant of a (4k+2)-dimensional (singly even-dimensional) framed differentiable manifold M, taking values in the 2-element group Z/2Z = {0,1}. The Kervaire invariant is defined as the Arf invariant
of the skew-quadratic form on the middle dimensional homology group. The Kervaire invariant problem is the
problem of determining in which dimensions the Kervaire invariant can be nonzero: this can happen in dimensions 2, 6, 14, 30, 62, and possibly 126, and in no other dimensions. The final case of dimension 126 remains open.
of the quadratic form
determined by the framing on the middle-dimensional Z/2Z-coefficient homology group
and is thus sometimes called the Arf–Kervaire invariant. The quadratic form (properly, skew-quadratic form) is a quadratic refinement of the usual ε-symmetric form on the middle dimensional homology of an (unframed) even-dimensional manifold; the framing yields the quadratic refinement.
The quadratic form q can be defined by algebraic topology using functional Steenrod squares, and geometrically via the self-intersections
of immersions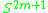
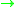
determined by the framing, or by the triviality/non-triviality of the normal bundles of embeddings 
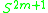
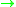
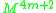(for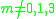 
) and the mod 2 Hopf invariant
of maps
(for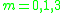
).
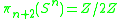of maps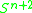 
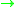
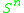(for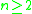 
), which is the cobordism group of surfaces embedded in 
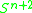with trivialized normal bundle.
used his invariant for n=10 to construct the Kervaire manifold
, a 10-dimensional PL manifold with no differentiable structure
, the first example of such a manifold, by showing that his invariant does not vanish on this PL manifold, but vanishes on all smooth manifolds of dimension 10.
, the skew-symmetric form is given by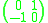
(with respect to the standard symplectic basis), and the skew-quadratic refinement is given by 
with respect to this basis: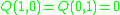 
: the basis curves don't self-link; and 
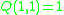: a (1,1) self-links, as in the Hopf fibration. This form thus has Arf invariant
0 (most of its elements have norm 0; it has isotropy index 1), and thus the standard embedded torus has Kervaire invariant 0.
proved that the Kervaire invariant is zero for manifolds of dimension 10, 18 proved that the Kervaire invariant can be nonzero zero for manifolds of dimension 6, 14 proved that the Kervaire invariant is zero for manifolds of dimension 8n+2 for n>1 proved that the Kervaire invariant can be nonzero for manifolds of dimension 30 proved that the Kervaire invariant is zero for manifolds of dimension n not of the form 2k − 2. showed that the Kervaire invariant is nonzero for some manifold of dimension 62. showed that the Kervaire invariant is zero for n-dimensional framed manifolds for n = 2k− 2 with k ≥ 8. They constructed a cohomology theory Ω with the following properties from which their result follows immediately:
Together these results imply that there are manifolds with nonzero Kervaire invariant manifolds in dimension 2, 6, 14, 30, 62, and none in all other dimensions other than 126. As of 2010 the case of dimension 126 is still open.
and a homomorphism from the 14th stable homotopy group of spheres onto Z/2Z. For n = 2, 6, 14 there is an
exotic framing on Sn/2 x Sn/2 with Kervaire-Milnor invariant 1.
Michel Kervaire
Michel André Kervaire was a French mathematician who made significant contributions to topology and algebra. He was the first to show the existence of topological n-manifolds with no differentiable structure , and computed the number of exotic spheres in dimensions greater than four...
, is defined in geometric topology
Geometric topology
In mathematics, geometric topology is the study of manifolds and maps between them, particularly embeddings of one manifold into another.- Topics :...
. It is an invariant of a (4k+2)-dimensional (singly even-dimensional) framed differentiable manifold M, taking values in the 2-element group Z/2Z = {0,1}. The Kervaire invariant is defined as the Arf invariant
Arf invariant
In mathematics, the Arf invariant of a nonsingular quadratic form over a field of characteristic 2 was defined by when he started the systematic study of quadratic forms over arbitrary fields of characteristic2. The Arf invariant is the substitute, in...
of the skew-quadratic form on the middle dimensional homology group. The Kervaire invariant problem is the
problem of determining in which dimensions the Kervaire invariant can be nonzero: this can happen in dimensions 2, 6, 14, 30, 62, and possibly 126, and in no other dimensions. The final case of dimension 126 remains open.
Definition
The Kervaire invariant is the Arf invariantArf invariant
In mathematics, the Arf invariant of a nonsingular quadratic form over a field of characteristic 2 was defined by when he started the systematic study of quadratic forms over arbitrary fields of characteristic2. The Arf invariant is the substitute, in...
of the quadratic form
Quadratic form
In mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,4x^2 + 2xy - 3y^2\,\!is a quadratic form in the variables x and y....
determined by the framing on the middle-dimensional Z/2Z-coefficient homology group
- q : H2m+1(M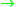;Z/2Z)
Z/2Z,
and is thus sometimes called the Arf–Kervaire invariant. The quadratic form (properly, skew-quadratic form) is a quadratic refinement of the usual ε-symmetric form on the middle dimensional homology of an (unframed) even-dimensional manifold; the framing yields the quadratic refinement.
The quadratic form q can be defined by algebraic topology using functional Steenrod squares, and geometrically via the self-intersections
of immersions
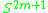
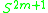
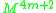determined by the framing, or by the triviality/non-triviality of the normal bundles of embeddings (for 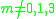) and the mod 2 Hopf invariantHopf invariant
In mathematics, in particular in algebraic topology, the Hopf invariant is a homotopy invariant of certain maps between spheres.- Motivation :In 1931 Heinz Hopf used Clifford parallels to construct the Hopf map\eta\colon S^3 \to S^2,...
of maps
(for
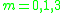).History
The Kervaire invariant is a generalization of the Arf invariant of a framed surface (= 2-dimensional manifold with stably trivialized tangent bundle) which was used by Pontryagin in 1950 to compute of the homotopy groupHomotopy group
In mathematics, homotopy groups are used in algebraic topology to classify topological spaces. The first and simplest homotopy group is the fundamental group, which records information about loops in a space...
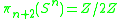of maps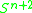 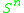(for 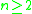), which is the cobordism group of surfaces embedded in 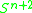with trivialized normal bundle.used his invariant for n=10 to construct the Kervaire manifold
Kervaire manifold
In mathematics, specifically in differential topology, a Kervaire manifold K4n+2 is a piecewise-linear manifold of dimension 4n+2 constructed by by plumbing together the tangent bundles of two 2n+1-spheres, and then gluing a ball to the result. In 10 dimensions this gives a piecewise-linear...
, a 10-dimensional PL manifold with no differentiable structure
Smooth structure
In mathematics, a smooth structure on a manifold allows for an unambiguous notion of smooth function. In particular, a smooth structure allows one to perform mathematical analysis on the manifold....
, the first example of such a manifold, by showing that his invariant does not vanish on this PL manifold, but vanishes on all smooth manifolds of dimension 10.
Examples
For the standard embedded torusTorus
In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
, the skew-symmetric form is given by
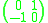(with respect to the standard symplectic basis), and the skew-quadratic refinement is given by 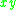with respect to this basis: 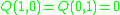: the basis curves don't self-link; and 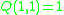: a (1,1) self-links, as in the Hopf fibration. This form thus has Arf invariantArf invariant
In mathematics, the Arf invariant of a nonsingular quadratic form over a field of characteristic 2 was defined by when he started the systematic study of quadratic forms over arbitrary fields of characteristic2. The Arf invariant is the substitute, in...
0 (most of its elements have norm 0; it has isotropy index 1), and thus the standard embedded torus has Kervaire invariant 0.
Kervaire invariant problem
The question of in which dimensions n there are n-dimensional framed manifolds of non-zero Kervaire invariant is called the Kervaire invariant problem. This is only possible if n is 2 mod 4.proved that the Kervaire invariant is zero for manifolds of dimension 10, 18 proved that the Kervaire invariant can be nonzero zero for manifolds of dimension 6, 14 proved that the Kervaire invariant is zero for manifolds of dimension 8n+2 for n>1 proved that the Kervaire invariant can be nonzero for manifolds of dimension 30 proved that the Kervaire invariant is zero for manifolds of dimension n not of the form 2k − 2. showed that the Kervaire invariant is nonzero for some manifold of dimension 62. showed that the Kervaire invariant is zero for n-dimensional framed manifolds for n = 2k− 2 with k ≥ 8. They constructed a cohomology theory Ω with the following properties from which their result follows immediately:
-
- The coefficient groups Ωn(point) have period 28=256 in n
- The coefficient groups Ωn(point) have a "gap": they vanish for n=1, 2, 3
- The coefficient groups Ωn(point) can detect non-vanishing Kervaire invariants: more precisely if the Kervaire invariant for manifolds of dimension n is nonzero then it has a nonzero image in Ω−n(point)
Together these results imply that there are manifolds with nonzero Kervaire invariant manifolds in dimension 2, 6, 14, 30, 62, and none in all other dimensions other than 126. As of 2010 the case of dimension 126 is still open.
Kervaire–Milnor invariant
The Kervaire–Milnor invariant is a closely related invariant of framed surgery of a 2, 6 or 14-dimensional framed manifold, that gives isomorphisms from the 2nd and 6th stable homotopy group of spheres to Z/2Z,and a homomorphism from the 14th stable homotopy group of spheres onto Z/2Z. For n = 2, 6, 14 there is an
exotic framing on Sn/2 x Sn/2 with Kervaire-Milnor invariant 1.
External links
- Slides and video of lecture by Hopkins at Edinburgh, 21 April, 2009
- Arf-Kervaire home page of Doug Ravenel
- Harvard-MIT Summer Seminar on the Kervaire Invariant
- 'Kervaire Invariant One Problem' Solved, April 23, 2009, blog post by John Baez and discussion, The n-Category Café
- Exotic spheres at the manifold atlas
Popular news stories
- Hypersphere Exotica: Kervaire Invariant Problem Has a Solution! A 45-year-old problem on higher-dimensional spheres is solved–probably, by Davide Castelvecchi, August 2009 Scientific AmericanScientific AmericanScientific American is a popular science magazine. It is notable for its long history of presenting science monthly to an educated but not necessarily scientific public, through its careful attention to the clarity of its text as well as the quality of its specially commissioned color graphics...
- Mathematicians solve 45-year-old Kervaire invariant puzzle, Erica Klarreich, 20 Jul 2009