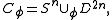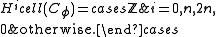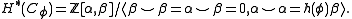Hopf invariant
Encyclopedia
In mathematics
, in particular in algebraic topology
, the Hopf invariant is a homotopy
invariant of certain maps between sphere
s.
used Clifford parallel
s to construct the Hopf map ,
,
and proved that is essential, i.e. not homotopic to the constant map, by using the linking number (=1) of the circles
is essential, i.e. not homotopic to the constant map, by using the linking number (=1) of the circles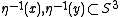 for any
for any  .
.
It was later shown that the homotopy group
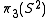 is the infinite cyclic group
is the infinite cyclic group
generated by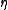 . In 1951, Jean-Pierre Serre
. In 1951, Jean-Pierre Serre
proved that the rational homotopy groups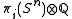
for an odd-dimensional sphere ( odd) are zero unless i = 0 or n. However, for an even-dimensional sphere (n even), there is one more bit of infinite cyclic homotopy in degree
odd) are zero unless i = 0 or n. However, for an even-dimensional sphere (n even), there is one more bit of infinite cyclic homotopy in degree 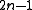 . There is an interesting way of seeing this:
. There is an interesting way of seeing this:
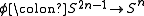 be a continuous map (assume
be a continuous map (assume 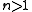 ). Then we can form the cell complex
). Then we can form the cell complex
where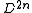 is a
is a 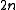 -dimensional disc attached to
-dimensional disc attached to 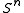 via
via 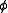 .
.
The cellular chain groups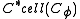 are just freely generated on the
are just freely generated on the  -cells in degree
-cells in degree  , so they are
, so they are 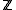 in degree 0,
in degree 0,  and
and 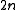 and zero everywhere else. Cellular (co-)homology is the (co-)homology of this chain complex
and zero everywhere else. Cellular (co-)homology is the (co-)homology of this chain complex
, and since all boundary homomorphisms must be zero (recall that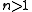 ), the cohomology is
), the cohomology is
Denote the generators of the cohomology groups by
For dimensional reasons, all cup-products between those classes must be trivial apart from . Thus, as a ring, the cohomology is
. Thus, as a ring, the cohomology is
The integer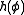 is the Hopf invariant of the map
is the Hopf invariant of the map 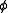 .
.
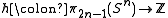 is a homomorphism. Moreover, if
is a homomorphism. Moreover, if  is even,
is even, 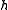 maps onto
maps onto 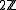 .
.
The Hopf invariant is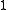 for the Hopf maps (where
for the Hopf maps (where 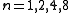 , corresponding to the real division algebras
, corresponding to the real division algebras 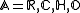 , respectively, and to the double cover
, respectively, and to the double cover 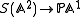 sending a direction on the sphere to the subspace it spans). It is a theorem, proved first by Frank Adams
sending a direction on the sphere to the subspace it spans). It is a theorem, proved first by Frank Adams
and subsequently by Michael Atiyah
with methods of K-theory
, that these are the only maps with Hopf invariant 1.
Let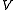 denote a vector space and
denote a vector space and 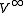 its one-point compactification, i.e.
its one-point compactification, i.e. 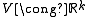 and
and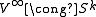 for some
for some 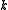 .
.
If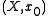 is any pointed space (as it is implicitly in the previous section), and if we take the point at infinity to be the basepoint of
is any pointed space (as it is implicitly in the previous section), and if we take the point at infinity to be the basepoint of 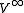 , then we can form the wedge products
, then we can form the wedge products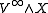 .
.
Now let
be a stable map, i.e. stable under the reduced suspension functor. The (stable) geometric Hopf invariant of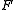 is
is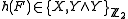 ,
,
an element of the stable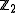 -equivariant homotopy group of maps from
-equivariant homotopy group of maps from 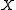 to
to 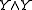 . Here "stable" means "stable under suspension", i.e. the direct limit over
. Here "stable" means "stable under suspension", i.e. the direct limit over 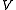 (or
(or 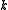 , if you will) of the ordinary, equivariant homotopy groups; and the
, if you will) of the ordinary, equivariant homotopy groups; and the 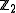 -action is the trivial action on
-action is the trivial action on 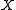 and the flipping of the two factors on
and the flipping of the two factors on 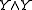 . If we let
. If we let
denote the canonical diagonal map and the identity, then the Hopf invariant is defined by the following:
the identity, then the Hopf invariant is defined by the following: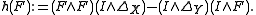
This map is initially a map from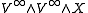 to
to 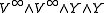 ,
,
but under the direct limit it becomes the advertised element of the stable homotopy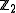 -equivariant group of maps.
-equivariant group of maps.
There exists also an unstable version of the Hopf invariant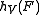 , for which one must keep track of the vector space
, for which one must keep track of the vector space 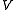 .
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, in particular in algebraic topology
Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
, the Hopf invariant is a homotopy
Homotopy
In topology, two continuous functions from one topological space to another are called homotopic if one can be "continuously deformed" into the other, such a deformation being called a homotopy between the two functions...
invariant of certain maps between sphere
Sphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
s.
Motivation
In 1931 Heinz HopfHeinz Hopf
Heinz Hopf was a German mathematician born in Gräbschen, Germany . He attended Dr. Karl Mittelhaus' higher boys' school from 1901 to 1904, and then entered the König-Wilhelm- Gymnasium in Breslau. He showed mathematical talent from an early age...
used Clifford parallel
Clifford parallel
A Clifford parallel is a line which lies at a constant distance from some "base" line but, unlike an ordinary parallel line, does not lie in the same plane...
s to construct the Hopf map
 ,
,and proved that
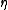 is essential, i.e. not homotopic to the constant map, by using the linking number (=1) of the circles
is essential, i.e. not homotopic to the constant map, by using the linking number (=1) of the circles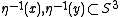 for any
for any  .
.It was later shown that the homotopy group
Homotopy group
In mathematics, homotopy groups are used in algebraic topology to classify topological spaces. The first and simplest homotopy group is the fundamental group, which records information about loops in a space...
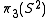 is the infinite cyclic group
is the infinite cyclic groupCyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
generated by
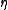 . In 1951, Jean-Pierre Serre
. In 1951, Jean-Pierre SerreJean-Pierre Serre
Jean-Pierre Serre is a French mathematician. He has made contributions in the fields of algebraic geometry, number theory, and topology.-Early years:...
proved that the rational homotopy groups
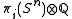
for an odd-dimensional sphere (
 odd) are zero unless i = 0 or n. However, for an even-dimensional sphere (n even), there is one more bit of infinite cyclic homotopy in degree
odd) are zero unless i = 0 or n. However, for an even-dimensional sphere (n even), there is one more bit of infinite cyclic homotopy in degree 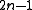 . There is an interesting way of seeing this:
. There is an interesting way of seeing this:Definition
Let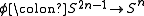 be a continuous map (assume
be a continuous map (assume 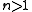 ). Then we can form the cell complex
). Then we can form the cell complexwhere
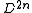 is a
is a 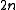 -dimensional disc attached to
-dimensional disc attached to 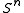 via
via 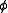 .
.The cellular chain groups
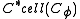 are just freely generated on the
are just freely generated on the  -cells in degree
-cells in degree  , so they are
, so they are 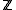 in degree 0,
in degree 0,  and
and 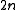 and zero everywhere else. Cellular (co-)homology is the (co-)homology of this chain complex
and zero everywhere else. Cellular (co-)homology is the (co-)homology of this chain complexChain complex
In mathematics, chain complex and cochain complex are constructs originally used in the field of algebraic topology. They are algebraic means of representing the relationships between the cycles and boundaries in various dimensions of some "space". Here the "space" could be a topological space or...
, and since all boundary homomorphisms must be zero (recall that
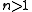 ), the cohomology is
), the cohomology isDenote the generators of the cohomology groups by
-
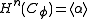 and
and 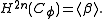
For dimensional reasons, all cup-products between those classes must be trivial apart from
 . Thus, as a ring, the cohomology is
. Thus, as a ring, the cohomology isThe integer
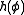 is the Hopf invariant of the map
is the Hopf invariant of the map 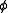 .
.Properties
Theorem: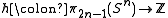 is a homomorphism. Moreover, if
is a homomorphism. Moreover, if  is even,
is even, 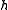 maps onto
maps onto 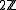 .
.The Hopf invariant is
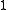 for the Hopf maps (where
for the Hopf maps (where 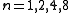 , corresponding to the real division algebras
, corresponding to the real division algebras 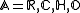 , respectively, and to the double cover
, respectively, and to the double cover 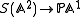 sending a direction on the sphere to the subspace it spans). It is a theorem, proved first by Frank Adams
sending a direction on the sphere to the subspace it spans). It is a theorem, proved first by Frank AdamsFrank Adams
John Frank Adams FRS was a British mathematician, one of the founders of homotopy theory.-Life:He was born in Woolwich, a suburb in south-east London. He began research as a student of Abram Besicovitch, but soon switched to algebraic topology. He received his Ph.D. from the University of...
and subsequently by Michael Atiyah
Michael Atiyah
Sir Michael Francis Atiyah, OM, FRS, FRSE is a British mathematician working in geometry.Atiyah grew up in Sudan and Egypt but spent most of his academic life in the United Kingdom at Oxford and Cambridge, and in the United States at the Institute for Advanced Study...
with methods of K-theory
K-theory
In mathematics, K-theory originated as the study of a ring generated by vector bundles over a topological space or scheme. In algebraic topology, it is an extraordinary cohomology theory known as topological K-theory. In algebra and algebraic geometry, it is referred to as algebraic K-theory. It...
, that these are the only maps with Hopf invariant 1.
Generalisations for stable maps
A very general notion of the Hopf invariant can be defined, but it requires a certain amount of homotopy theoretic groundwork:Let
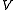 denote a vector space and
denote a vector space and 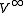 its one-point compactification, i.e.
its one-point compactification, i.e. 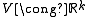 and
and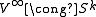 for some
for some 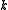 .
.If
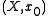 is any pointed space (as it is implicitly in the previous section), and if we take the point at infinity to be the basepoint of
is any pointed space (as it is implicitly in the previous section), and if we take the point at infinity to be the basepoint of 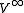 , then we can form the wedge products
, then we can form the wedge products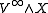 .
.Now let

be a stable map, i.e. stable under the reduced suspension functor. The (stable) geometric Hopf invariant of
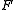 is
is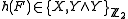 ,
,an element of the stable
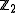 -equivariant homotopy group of maps from
-equivariant homotopy group of maps from 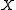 to
to 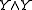 . Here "stable" means "stable under suspension", i.e. the direct limit over
. Here "stable" means "stable under suspension", i.e. the direct limit over 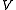 (or
(or 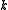 , if you will) of the ordinary, equivariant homotopy groups; and the
, if you will) of the ordinary, equivariant homotopy groups; and the 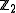 -action is the trivial action on
-action is the trivial action on 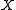 and the flipping of the two factors on
and the flipping of the two factors on 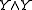 . If we let
. If we let
denote the canonical diagonal map and
 the identity, then the Hopf invariant is defined by the following:
the identity, then the Hopf invariant is defined by the following: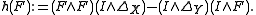
This map is initially a map from
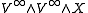 to
to 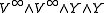 ,
,but under the direct limit it becomes the advertised element of the stable homotopy
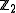 -equivariant group of maps.
-equivariant group of maps.There exists also an unstable version of the Hopf invariant
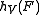 , for which one must keep track of the vector space
, for which one must keep track of the vector space 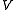 .
.