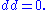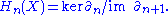Chain complex
Encyclopedia
In mathematics
, chain complex and cochain complex are constructs originally used in the field of algebraic topology
. They are algebraic means of representing the relationships between the cycles and boundaries in various dimensions of some "space". Here the "space" could be a topological space
or an algebraic construction such as a simplicial complex
. More generally, homological algebra
includes the study of chain complexes in the abstract, without any reference to an underlying space. In this case, chain complexes are studied axiomatically as algebraic structure
s.
Applications of chain complexes usually define and apply their homology groups (cohomology groups for cochain complexes); in more abstract settings various equivalence relations are applied to complexes (for example starting with the chain homotopy idea). Chain complexes are easily defined in abelian categories, also.
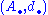is a sequence of abelian group
s or modules
... A2, A1, A0, A-1, A-2, ... connected by homomorphism
s (called boundary operators) dn : An→An−1, such that the composition of any two consecutive maps is zero: dn ∘ dn+1 = 0 for all n. They are usually written out as:
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, chain complex and cochain complex are constructs originally used in the field of algebraic topology
Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
. They are algebraic means of representing the relationships between the cycles and boundaries in various dimensions of some "space". Here the "space" could be a topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
or an algebraic construction such as a simplicial complex
Simplicial complex
In mathematics, a simplicial complex is a topological space of a certain kind, constructed by "gluing together" points, line segments, triangles, and their n-dimensional counterparts...
. More generally, homological algebra
Homological algebra
Homological algebra is the branch of mathematics which studies homology in a general algebraic setting. It is a relatively young discipline, whose origins can be traced to investigations in combinatorial topology and abstract algebra at the end of the 19th century, chiefly by Henri Poincaré and...
includes the study of chain complexes in the abstract, without any reference to an underlying space. In this case, chain complexes are studied axiomatically as algebraic structure
Algebraic structure
In abstract algebra, an algebraic structure consists of one or more sets, called underlying sets or carriers or sorts, closed under one or more operations, satisfying some axioms. Abstract algebra is primarily the study of algebraic structures and their properties...
s.
Applications of chain complexes usually define and apply their homology groups (cohomology groups for cochain complexes); in more abstract settings various equivalence relations are applied to complexes (for example starting with the chain homotopy idea). Chain complexes are easily defined in abelian categories, also.
Formal definition
A chain complex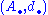 is a sequence of abelian groupAbelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
s or modules
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
... A2, A1, A0, A-1, A-2, ... connected by homomorphism
Homomorphism
In abstract algebra, a homomorphism is a structure-preserving map between two algebraic structures . The word homomorphism comes from the Greek language: ὁμός meaning "same" and μορφή meaning "shape".- Definition :The definition of homomorphism depends on the type of algebraic structure under...
s (called boundary operators) dn : An→An−1, such that the composition of any two consecutive maps is zero: dn ∘ dn+1 = 0 for all n. They are usually written out as:
-
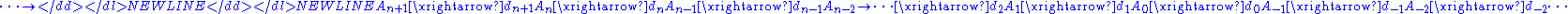
A variant on the concept of chain complex is that of cochain complex. A cochain complex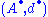
is a sequence of abelian groupAbelian groupIn abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
s or modulesModule (mathematics)In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
...,
, 
, 
, 
, 
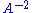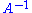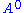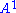, ... connected by homomorphismHomomorphismIn abstract algebra, a homomorphism is a structure-preserving map between two algebraic structures . The word homomorphism comes from the Greek language: ὁμός meaning "same" and μορφή meaning "shape".- Definition :The definition of homomorphism depends on the type of algebraic structure under...
s
such that the composition of any two consecutive maps is zero: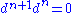 
for all n:
-
The idea is basically the same. In either case, the index
in 
resp.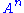 
is referred to as the degree (or dimension).
A bounded chain complex is one in which almost allAlmost allIn mathematics, the phrase "almost all" has a number of specialised uses."Almost all" is sometimes used synonymously with "all but finitely many" or "all but a countable set" ; see almost....
the Ai are 0; i.e., a finite complex extended to the left and right by 0's. An example is the complex defining the homology theoryHomology theoryIn mathematics, homology theory is the axiomatic study of the intuitive geometric idea of homology of cycles on topological spaces. It can be broadly defined as the study of homology theories on topological spaces.-The general idea:...
of a (finite) simplicial complexSimplicial complexIn mathematics, a simplicial complex is a topological space of a certain kind, constructed by "gluing together" points, line segments, triangles, and their n-dimensional counterparts...
. A chain complex is bounded above if all degrees above some fixed degree N are 0, and is bounded below if all degrees below some fixed degree are 0. Clearly, a complex is bounded above and below if and only ifIf and only ifIn logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
the complex is bounded.
Fundamental terminology
Leaving out the indices, the basic relation on d can be thought of as
The elements of the individual groups of a chain complex are called chains (or cochains in the case of a cochain complex.) The imageImage (mathematics)In mathematics, an image is the subset of a function's codomain which is the output of the function on a subset of its domain. Precisely, evaluating the function at each element of a subset X of the domain produces a set called the image of X under or through the function...
of d is the group of boundaries, or in a cochain complex, coboundaries. The kernelKernel (mathematics)In mathematics, the word kernel has several meanings. Kernel may mean a subset associated with a mapping:* The kernel of a mapping is the set of elements that map to the zero element , as in kernel of a linear operator and kernel of a matrix...
of d (i.e., the subgroup sent to 0 by d) is the group of cycles, or in the case of a cochain complex, cocycles. From the basic relation, the (co)boundaries lie inside the (co)cycles. This phenomenon is studied in a systematic way using (coCohomologyIn mathematics, specifically in algebraic topology, cohomology is a general term for a sequence of abelian groups defined from a co-chain complex. That is, cohomology is defined as the abstract study of cochains, cocycles, and coboundaries...
)homology groups.
Singular homology
Suppose we are given a topological spaceTopological spaceTopological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
X.
Define Cn(X) for naturalNatural numberIn mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
n to be the free abelian groupFree abelian groupIn abstract algebra, a free abelian group is an abelian group that has a "basis" in the sense that every element of the group can be written in one and only one way as a finite linear combination of elements of the basis, with integer coefficients. Hence, free abelian groups over a basis B are...
formally generated by singular n-simplicesSingular homologyIn algebraic topology, a branch of mathematics, singular homology refers to the study of a certain set of algebraic invariants of a topological space X, the so-called homology groups H_n....
in X, and define the boundary map
-
where the hat denotes the omission of a vertexVertex (geometry)In geometry, a vertex is a special kind of point that describes the corners or intersections of geometric shapes.-Of an angle:...
. That is, the boundary of a singular simplex is alternating sum of restrictions to its faces. It can be shown ∂² = 0, so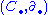
is a chain complex; the singular homologySingular homologyIn algebraic topology, a branch of mathematics, singular homology refers to the study of a certain set of algebraic invariants of a topological space X, the so-called homology groups H_n....
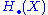is the homology of this complex; that is,
de Rham cohomology
The differential k-forms on any smooth manifold M form an abelian groupAbelian groupIn abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
(in fact an RReal numberIn mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
-vector spaceVector spaceA vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
) called Ωk(M) under additionAdditionAddition is a mathematical operation that represents combining collections of objects together into a larger collection. It is signified by the plus sign . For example, in the picture on the right, there are 3 + 2 apples—meaning three apples and two other apples—which is the same as five apples....
.
The exterior derivativeExterior derivativeIn differential geometry, the exterior derivative extends the concept of the differential of a function, which is a 1-form, to differential forms of higher degree. Its current form was invented by Élie Cartan....
dk maps Ωk(M) to Ωk+1(M), and d 2 = 0 follows essentially from symmetry of second derivativesSymmetry of second derivativesIn mathematics, the symmetry of second derivatives refers to the possibility of interchanging the order of taking partial derivatives of a functionfof n variables...
, so the vector spaceVector spaceA vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
s of k-forms along with the exterior derivative are a cochain complex:
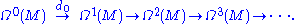
The homology of this complex is the de Rham cohomology
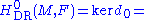{locally constant functionConstant functionIn mathematics, a constant function is a function whose values do not vary and thus are constant. For example the function f = 4 is constant since f maps any value to 4...
s on M with values in F}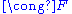
#{connected pieces of M}
Chain maps
A chain map f between two chain complexes
and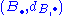 
is a sequence 
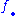of module homomorphismsModule (mathematics)In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
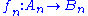for each n that intertwines with the differentials on the two chain complexes: 
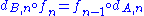. Such a map sends cycles to cycles and boundaries to boundaries, and thus descends to a map on homology:
.
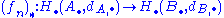A continuous map of topological spaces induces chain maps in both the singular and de Rham chain complexes described above (and in general for the chain complex defining any homology theoryHomology theoryIn mathematics, homology theory is the axiomatic study of the intuitive geometric idea of homology of cycles on topological spaces. It can be broadly defined as the study of homology theories on topological spaces.-The general idea:...
of topological spaces) and thus a continuous map induces a map on homology. Because the map induced on a composition of maps is the composition of the induced maps, these homology theories are functorFunctorIn category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
s from the category of topological spaces with continuous maps to the category of abelian groups with group homomorphisms.
It is worth noticing that the concept of chain map reduces to the one of boundary through the construction of the coneMapping cone (homological algebra)In homological algebra, the mapping cone is a construction on a map of chain complexes inspired by the analogous construction in topology. In the theory of triangulated categories it is a kind of combined kernel and cokernel: if the chain complexes take their terms in an abelian category, so that...
of a chain map.
Chain homotopy
Chain homotopies give an important equivalence relation between chain maps. Chain homotopic chain maps induce the same maps on homology groups. A particular case is that homotopic maps between two spaces X and Y induce the same maps from homology of X to homology of Y. Chain homotopies have a geometric interpretation; it is described, for example, in the book of Bott and Tu. See Homotopy category of chain complexesHomotopy category of chain complexesIn homological algebra in mathematics, the homotopy category K of chain complexes in an additive category A is a framework for working with chain homotopies and homotopy equivalences...
for further information.-
-
-
