Homotopy category of chain complexes
Encyclopedia
In homological algebra
in mathematics
, the homotopy category K(A) of chain complexes in an additive category
A is a framework for working with chain homotopies and homotopy equivalences. It lies intermediate between the category of chain complexes Kom(A) of A and the derived category
D(A) of A when A is abelian
; unlike the former it is a triangulated category
, and unlike the latter its formation does not require that A is abelian. Philosophically, while D(A) makes isomorphisms of any maps of complexes that are quasi-isomorphism
s in Kom(A), K(A) does so only for those that are quasi-isomorphisms for a "good reason", namely actually having an inverse up to homotopy equivalence. Thus, K(A) is more understandable than D(A).
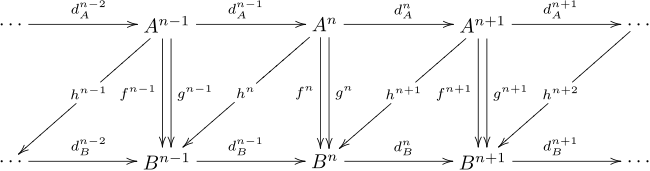
. The homotopy category K(A) is based on the following definition: if we have complexes A, B and maps f, g from A to B, a chain homotopy from f to g is a collection of maps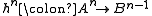
(not a map of complexes) such that
or simply 
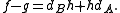
This can be depicted as:
We also say that f and g are chain homotopic, or that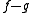
is null-homotopic or homotopic to 0. It is clear from the definition that the maps of complexes which are null-homotopic form a group.
The homotopy category of chain complexes K(A) is then defined as follows: its objects are the same as the objects of Kom(A), namely chain complex
es. Its morphisms are "maps of complexes modulo homotopy": that is, we define an equivalence relation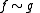
if f is homotopic to g
and define
to be the quotient
by this relation. It is clearer that this results in an additive category if one notes that this is the same as taking the quotient by the subgroup of null-homotopic maps.
The following variants of the definition are also widely used: if one takes only bounded-below (An=0 for n<<0), bounded-above (An=0 for n>>0), or bounded (An=0 for |n|>>0) complexes instead of unbounded ones, one speaks of the bounded-below homotopy category etc. They are denoted by K+(A), K-(A) and Kb(A), respectively.
A morphism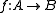
which is an isomorphism in K(A) is called a homotopy equivalence. In detail, this means there is another map 
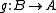, such that the two compositions are homotopic to the identities: 
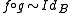and
.
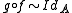The name "homotopy" comes from the fact that homotopic maps of topological space
s induce homotopic (in the above sense) maps of singular chains.
. (The converse is false in general.) This shows that there is a canonical functor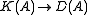
to the derived category
(if A is abelian
).
(note that 
),
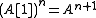where the differential is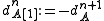
.
For the cone of a morphism f we take the mapping cone
. There are natural maps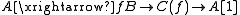
This diagram is called a triangle. The homotopy category K(A) is a triangulated category
, if one defines distinguished triangles to be isomorphic (in K(A), i.e. homotopy equivalent) to the triangles above, for arbitrary A, B and f. The same is true for the bounded variants K+(A), K-(A) and Kb(A). Although triangles make sense in Kom(A) as well, that category is not triangulated with respect to these distinguished triangles; for example,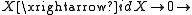
is not distinguished since the cone of the identity map is not isomorphic to the complex 0 (however, the zero map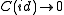
is a homotopy equivalence, so that this triangle is distinguished in K(A)). Less trivially, the rotation of a distinguished triangle is obviously not distinguished in Kom(A), but (less obviously so) is distinguished in K(A). See the references for details.
C is defined to have the same objects as C, but morphisms are defined by
. (This boils down to the homotopy of chain complexes if C is the category of complexes whose morphisms do not have to respect the differentials). If C has cones and shifts in a suitable sense, then Ho C is a triangulated category, too.
Homological algebra
Homological algebra is the branch of mathematics which studies homology in a general algebraic setting. It is a relatively young discipline, whose origins can be traced to investigations in combinatorial topology and abstract algebra at the end of the 19th century, chiefly by Henri Poincaré and...
in mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the homotopy category K(A) of chain complexes in an additive category
Additive category
In mathematics, specifically in category theory, an additive category is a preadditive category C such that all finite collections of objects A1,...,An of C have a biproduct A1 ⊕ ⋯ ⊕ An in C....
A is a framework for working with chain homotopies and homotopy equivalences. It lies intermediate between the category of chain complexes Kom(A) of A and the derived category
Derived category
In mathematics, the derived category D of an abelian category C is a construction of homological algebra introduced to refine and in a certain sense to simplify the theory of derived functors defined on C...
D(A) of A when A is abelian
Abelian category
In mathematics, an abelian category is a category in which morphisms and objects can be added and in which kernels and cokernels exist and have desirable properties. The motivating prototype example of an abelian category is the category of abelian groups, Ab. The theory originated in a tentative...
; unlike the former it is a triangulated category
Triangulated category
A triangulated category is a mathematical category satisfying some axioms that are based on the properties of the homotopy category of spectra, and the derived category of an abelian category. A t-category is a triangulated category with a t-structure.- History :The notion of a derived category...
, and unlike the latter its formation does not require that A is abelian. Philosophically, while D(A) makes isomorphisms of any maps of complexes that are quasi-isomorphism
Quasi-isomorphism
In homological algebra, a branch of mathematics, a quasi-isomorphism is a morphism A → B of chain complexes such that the induced morphisms...
s in Kom(A), K(A) does so only for those that are quasi-isomorphisms for a "good reason", namely actually having an inverse up to homotopy equivalence. Thus, K(A) is more understandable than D(A).
Definitions
Let A be an additive categoryAdditive category
In mathematics, specifically in category theory, an additive category is a preadditive category C such that all finite collections of objects A1,...,An of C have a biproduct A1 ⊕ ⋯ ⊕ An in C....
. The homotopy category K(A) is based on the following definition: if we have complexes A, B and maps f, g from A to B, a chain homotopy from f to g is a collection of maps
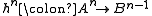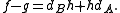
(not a map of complexes) such that or simply This can be depicted as:
We also say that f and g are chain homotopic, or that
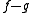is null-homotopic or homotopic to 0. It is clear from the definition that the maps of complexes which are null-homotopic form a group.The homotopy category of chain complexes K(A) is then defined as follows: its objects are the same as the objects of Kom(A), namely chain complex
Chain complex
In mathematics, chain complex and cochain complex are constructs originally used in the field of algebraic topology. They are algebraic means of representing the relationships between the cycles and boundaries in various dimensions of some "space". Here the "space" could be a topological space or...
es. Its morphisms are "maps of complexes modulo homotopy": that is, we define an equivalence relation
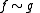if f is homotopic to gand define
to be the quotient
Quotient
In mathematics, a quotient is the result of division. For example, when dividing 6 by 3, the quotient is 2, while 6 is called the dividend, and 3 the divisor. The quotient further is expressed as the number of times the divisor divides into the dividend e.g. The quotient of 6 and 2 is also 3.A...
by this relation. It is clearer that this results in an additive category if one notes that this is the same as taking the quotient by the subgroup of null-homotopic maps.
The following variants of the definition are also widely used: if one takes only bounded-below (An=0 for n<<0), bounded-above (An=0 for n>>0), or bounded (An=0 for |n|>>0) complexes instead of unbounded ones, one speaks of the bounded-below homotopy category etc. They are denoted by K+(A), K-(A) and Kb(A), respectively.
A morphism
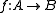which is an isomorphism in K(A) is called a homotopy equivalence. In detail, this means there is another map 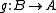, such that the two compositions are homotopic to the identities: 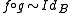and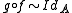.The name "homotopy" comes from the fact that homotopic maps of topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
s induce homotopic (in the above sense) maps of singular chains.
Remarks
Two chain homotopic maps f and g induce the same maps on homology because (f − g) sends cycles to boundaries, which are zero in homology. In particular a homotopy equivalence is a quasi-isomorphismQuasi-isomorphism
In homological algebra, a branch of mathematics, a quasi-isomorphism is a morphism A → B of chain complexes such that the induced morphisms...
. (The converse is false in general.) This shows that there is a canonical functor
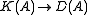to the derived categoryDerived category
In mathematics, the derived category D of an abelian category C is a construction of homological algebra introduced to refine and in a certain sense to simplify the theory of derived functors defined on C...
(if A is abelian
Abelian category
In mathematics, an abelian category is a category in which morphisms and objects can be added and in which kernels and cokernels exist and have desirable properties. The motivating prototype example of an abelian category is the category of abelian groups, Ab. The theory originated in a tentative...
).
The triangulated structure
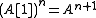The shift A[1] of a complex A is the following complex (note that ),where the differential is
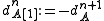.For the cone of a morphism f we take the mapping cone
Mapping cone (homological algebra)
In homological algebra, the mapping cone is a construction on a map of chain complexes inspired by the analogous construction in topology. In the theory of triangulated categories it is a kind of combined kernel and cokernel: if the chain complexes take their terms in an abelian category, so that...
. There are natural maps
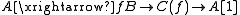
This diagram is called a triangle. The homotopy category K(A) is a triangulated category
Triangulated category
A triangulated category is a mathematical category satisfying some axioms that are based on the properties of the homotopy category of spectra, and the derived category of an abelian category. A t-category is a triangulated category with a t-structure.- History :The notion of a derived category...
, if one defines distinguished triangles to be isomorphic (in K(A), i.e. homotopy equivalent) to the triangles above, for arbitrary A, B and f. The same is true for the bounded variants K+(A), K-(A) and Kb(A). Although triangles make sense in Kom(A) as well, that category is not triangulated with respect to these distinguished triangles; for example,
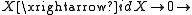
is not distinguished since the cone of the identity map is not isomorphic to the complex 0 (however, the zero map
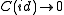is a homotopy equivalence, so that this triangle is distinguished in K(A)). Less trivially, the rotation of a distinguished triangle is obviously not distinguished in Kom(A), but (less obviously so) is distinguished in K(A). See the references for details.Generalization
More generally, the homotopy category Ho C of a differential graded categoryDifferential graded category
In mathematics, especially homological algebra, a differential graded category or DG category for short, is a category whose morphism sets are endowed with the additional structure of a differential graded Z-module....
C is defined to have the same objects as C, but morphisms are defined by
. (This boils down to the homotopy of chain complexes if C is the category of complexes whose morphisms do not have to respect the differentials). If C has cones and shifts in a suitable sense, then Ho C is a triangulated category, too.