
Quasi-isomorphism
Encyclopedia
In homological algebra
, a branch of mathematics
, a quasi-isomorphism is a morphism A → B of chain complex
es (respectively, cochain complexes) such that the induced morphisms
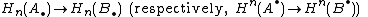
of homology
groups (respectively, of cohomology groups) are isomorphisms for all n.
, quasi-isomorphisms are sometimes used as the class of weak equivalence
s when the objects of the category are chain or cochain complexes. This results in a homology-local theory, in the sense of Bousfield localization in homotopy theory.
Quasi-isomorphisms play the fundamental role in defining the derived category
of an abelian category
.
Homological algebra
Homological algebra is the branch of mathematics which studies homology in a general algebraic setting. It is a relatively young discipline, whose origins can be traced to investigations in combinatorial topology and abstract algebra at the end of the 19th century, chiefly by Henri Poincaré and...
, a branch of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a quasi-isomorphism is a morphism A → B of chain complex
Chain complex
In mathematics, chain complex and cochain complex are constructs originally used in the field of algebraic topology. They are algebraic means of representing the relationships between the cycles and boundaries in various dimensions of some "space". Here the "space" could be a topological space or...
es (respectively, cochain complexes) such that the induced morphisms
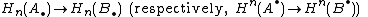
of homology
Homology (mathematics)
In mathematics , homology is a certain general procedure to associate a sequence of abelian groups or modules with a given mathematical object such as a topological space or a group...
groups (respectively, of cohomology groups) are isomorphisms for all n.
Applications
In the theory of model categoriesModel category
In mathematics, particularly in homotopy theory, a model category is a category with distinguished classes of morphisms called 'weak equivalences', 'fibrations' and 'cofibrations'. These abstract from a conventional homotopy category, of topological spaces or of chain complexes...
, quasi-isomorphisms are sometimes used as the class of weak equivalence
Weak equivalence
-Mathematics:In mathematics, a weak equivalence is a notion from homotopy theory which in some sense identifies objects that have the same basic "shape"...
s when the objects of the category are chain or cochain complexes. This results in a homology-local theory, in the sense of Bousfield localization in homotopy theory.
Quasi-isomorphisms play the fundamental role in defining the derived category
Derived category
In mathematics, the derived category D of an abelian category C is a construction of homological algebra introduced to refine and in a certain sense to simplify the theory of derived functors defined on C...
of an abelian category
Abelian category
In mathematics, an abelian category is a category in which morphisms and objects can be added and in which kernels and cokernels exist and have desirable properties. The motivating prototype example of an abelian category is the category of abelian groups, Ab. The theory originated in a tentative...
.

