Mathematics

In mathematics

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, a weak equivalence is a notion from homotopy theory which in some sense identifies objects that have the same basic "shape". This notion is formalized in the axiom

Axiom

In traditional logic, an axiom or postulate is a proposition that is not proven or demonstrated but considered either to be self-evident or to define and delimit the realm of analysis. In other words, an axiom is a logical statement that is assumed to be true...

atic definition of a closed model category.

A closed model category by definition contains a class of morphism

Morphism

In mathematics, a morphism is an abstraction derived from structure-preserving mappings between two mathematical structures. The notion of morphism recurs in much of contemporary mathematics...

s called weak equivalences, and these morphisms become isomorphism

Isomorphism

In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations.  If there exists an isomorphism between two structures, the two structures are said to be isomorphic.  In a certain sense, isomorphic structures are...

s upon passing to the associated homotopy category. In particular, if the weak equivalences of two model categories containing the same objects and morphisms are defined in the same way, the resulting homotopy categories will be the same, regardless of the definitions of fibration

Fibration

In topology, a branch of mathematics, a fibration is a generalization of the notion of a fiber bundle. A fiber bundle makes precise the idea of one topological space being "parameterized" by another topological space . A fibration is like a fiber bundle, except that the fibers need not be the same...

s and cofibration

Cofibration

In mathematics, in particular homotopy theory, a continuous mappingi\colon A \to X,where A and X are topological spaces, is a cofibration if it satisfies the homotopy extension property with respect to all spaces Y. The name is because the dual condition, the homotopy lifting property, defines...

s in the respective categories.

Different model categories define weak equivalences differently. For example, in the category of (bounded) chain complex

Chain complex

In mathematics, chain complex and cochain complex are constructs originally used in the field of algebraic topology. They are algebraic means of representing the relationships between the cycles and boundaries in various dimensions of some "space". Here the "space" could be a topological space or...

es, one might define a model structure where the weak equivalences are those morphisms


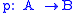
where


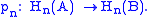
are isomorphisms for all n ≥ 0. However, this is not the only possible choice of weak equivalences for this category: one could also define the class of weak equivalences to be those maps that are chain homotopy equivalences of complexes.

For another example, the category of CW complex

CW complex

In topology, a CW complex is a type of topological space introduced by J. H. C. Whitehead to meet the needs of homotopy theory. This class of spaces is broader and has some better categorical properties than simplicial complexes, but still retains a combinatorial naturethat allows for...

es can be given the structure of a model category where the weak equivalences are the weak homotopy equivalences i.e. those morphisms X → Y that induce isomorphisms in homotopy group

Homotopy group

In mathematics, homotopy groups are used in algebraic topology to classify topological spaces. The first and simplest homotopy group is the fundamental group, which records information about loops in a space...

s


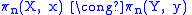
for all choices of basepoints x ∈ X, y ∈ Y, and all n ≥ 0.

A fibration

Fibration

In topology, a branch of mathematics, a fibration is a generalization of the notion of a fiber bundle. A fiber bundle makes precise the idea of one topological space being "parameterized" by another topological space . A fibration is like a fiber bundle, except that the fibers need not be the same...

 which is also a weak equivalence is also known as a trivial (or acyclic) fibration. A cofibration

Cofibration

In mathematics, in particular homotopy theory, a continuous mappingi\colon A \to X,where A and X are topological spaces, is a cofibration if it satisfies the homotopy extension property with respect to all spaces Y. The name is because the dual condition, the homotopy lifting property, defines...

 which is also a weak equivalence is also known as a trivial (or acyclic) cofibration.

Formal Languages

In formal language theory, weak equivalence of two grammars means they generate the same set of strings, i.e. that the formal language

Formal language

A formal language is a set of words—that is, finite strings of letters, symbols, or tokens that are defined in the language. The set from which these letters are taken is the alphabet over which the language is defined. A formal language is often defined by means of a formal grammar...

 they generate is the same. In compiler theory the notion is distinguished from strong (or structural) equivalence which additionally means that the two parse tree

Parse tree

A concrete syntax tree or parse tree or parsing treeis an ordered, rooted tree that represents the syntactic structure of a string according to some formal grammar. In a parse tree, the interior nodes are labeled by non-terminals of the grammar, while the leaf nodes are labeled by terminals of the...

s are reasonably similar in that the same semantic interpretation can be assigned to both.

Vijay-Shanker and Weir (1994) demonstrates that Linear Indexed Grammars

Indexed grammar

An indexed grammar is a formal grammar which describes indexed languages. They have three disjoint sets of symbols: the usual terminals and nonterminals, as well as index symbols, which appear only in intermediate derivation steps on a stack associated with the non-terminals of that step.The...

, Combinatory Categorial Grammars

Combinatory categorial grammar

Combinatory categorial grammar is an efficiently parseable, yet linguistically expressive grammar formalism. It has a transparent interface between surface syntax and underlying semantic representation, including predicate-argument structure, quantification and information structure.CCG relies on...

, Tree-adjoining Grammars

Tree-adjoining grammar

Tree-adjoining grammar is a grammar formalism defined by Aravind Joshi. Tree-adjoining grammars are somewhat similar to context-free grammars, but the elementary unit of rewriting is the tree rather than the symbol...

, and Head Grammars

Head grammar

Head Grammar is a grammar formalism introduced in Carl Pollard as an extension of the Context-free grammar class of grammars. The class of head grammars is a subset of the linear context-free rewriting systems....

 are weakly equivalent formalisms, in that the all define the same string languages.

On the other hand, if the two grammars generate the same set of derivation trees (or more generally, the same set of abstract syntactic objects), then the two languages are strongly equivalent. Chomsky (1963) introduces the notion of strong equivalence, and argues that only strong equivalence is relevant when comparing grammar formalisms. Kornai and Pullum (1990) and Miller (1994) offer a refined notion of strong equivalence that allows for isomorphic relationships between the syntactic analyses given by different formalisms. Yoshinaga, Miyao, and Tsujii (2002) offers a proof of the strong equivalency of the LTAG

Tree-adjoining grammar

Tree-adjoining grammar is a grammar formalism defined by Aravind Joshi. Tree-adjoining grammars are somewhat similar to context-free grammars, but the elementary unit of rewriting is the tree rather than the symbol...

 and HPSG

Head-driven phrase structure grammar

Head-driven phrase structure grammar is a highly lexicalized, non-derivational generative grammar theory developed by Carl Pollard and Ivan Sag. It is the immediate successor to generalized phrase structure grammar. HPSG draws from other fields such as computer science and uses Ferdinand de...

formalisms.