Differential graded category
Encyclopedia
In mathematics
, especially homological algebra
, a differential graded category or DG category for short, is a category
whose morphism sets are endowed with the additional structure of a differential graded Z-module.
In detail, this means that
, the morphisms from any object A to another object B of the category is a direct sum 
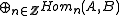and there is a differential d on this graded group, i.e. for all n a linear map 
, which has to satisfy 
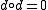. This is equivalent to saying that 
is a cochain complex. Furthermore, the composition of morphisms
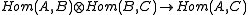is required to be a map of complexes, and for all objects A of the category, one requires 
.
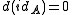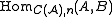is the group of maps 
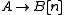which do not need to respect the differentials of the complexes A and B, i.e. 
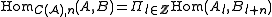. The differential of such a morphism 
of degree n is defined to be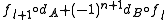 
, where 
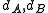are the differentials of A and B, respectively. This applies to the category of complexes of quasi-coherent sheaves on a scheme
over a ring.
structure such that weak equivalences are those functors that induce an equivalence of derived categories
.
Given a dg-category C over some ring R, there is a notion of smoothness and properness of C that reduces to the usual notions of smooth and proper morphisms in case C is the category of quasi-coherent sheaves on some scheme X over R.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, especially homological algebra
Homological algebra
Homological algebra is the branch of mathematics which studies homology in a general algebraic setting. It is a relatively young discipline, whose origins can be traced to investigations in combinatorial topology and abstract algebra at the end of the 19th century, chiefly by Henri Poincaré and...
, a differential graded category or DG category for short, is a category
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
whose morphism sets are endowed with the additional structure of a differential graded Z-module.
In detail, this means that
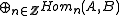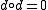, the morphisms from any object A to another object B of the category is a direct sum and there is a differential d on this graded group, i.e. for all n a linear map , which has to satisfy . This is equivalent to saying that is a cochain complex. Furthermore, the composition of morphisms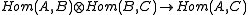 is required to be a map of complexes, and for all objects A of the category, one requires 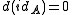.Examples
- Any additive category may be considered to be a DG-category by imposing the trivial grading (i.e. all
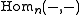vanish for n ≠ 0) and trivial differential (d = 0). - A little bit more sophisticated is the category of complexes
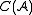over an additive category 
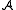. By definition,
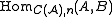is the group of maps 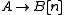which do not need to respect the differentials of the complexes A and B, i.e. 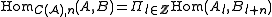. The differential of such a morphism of degree n is defined to be 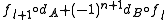, where 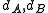are the differentials of A and B, respectively. This applies to the category of complexes of quasi-coherent sheaves on a schemeScheme (mathematics)
In mathematics, a scheme is an important concept connecting the fields of algebraic geometry, commutative algebra and number theory. Schemes were introduced by Alexander Grothendieck so as to broaden the notion of algebraic variety; some consider schemes to be the basic object of study of modern...
over a ring.
- A DG-category with one object is the same as a DG-ring.
Further properties
The category of small dg-categories can be endowed with a model categoryModel category
In mathematics, particularly in homotopy theory, a model category is a category with distinguished classes of morphisms called 'weak equivalences', 'fibrations' and 'cofibrations'. These abstract from a conventional homotopy category, of topological spaces or of chain complexes...
structure such that weak equivalences are those functors that induce an equivalence of derived categories
Derived category
In mathematics, the derived category D of an abelian category C is a construction of homological algebra introduced to refine and in a certain sense to simplify the theory of derived functors defined on C...
.
Given a dg-category C over some ring R, there is a notion of smoothness and properness of C that reduces to the usual notions of smooth and proper morphisms in case C is the category of quasi-coherent sheaves on some scheme X over R.