
Triangulated category
Encyclopedia
A triangulated category is a mathematical
category
satisfying some axiom
s that are based on the properties of the homotopy category of spectra
, and the derived category
of an abelian category
. A t-category is a triangulated category with a t-structure.

and likewise for morphisms from X to Y.
A triangle (X, Y, Z, u, v, w) is a set of 3 objects X, Y, and Z, together with morphisms u from X to Y, v from Y to Z and w from Z to X[1]. Triangles are generally written in the unravelled form:
There are two ways to rotate the above triangle: or
or 
These axioms are not entirely independent, since (TR 3) can be derived from the others.
 to indicate that they are of "degree 1"; e.g. the map from Z′ to X is in fact from Z′ to T(X). The octahedral axiom then asserts the existence of maps f and g forming a distinguished triangle, and so that f and g form commutative triangles in the other faces which contain them:
to indicate that they are of "degree 1"; e.g. the map from Z′ to X is in fact from Z′ to T(X). The octahedral axiom then asserts the existence of maps f and g forming a distinguished triangle, and so that f and g form commutative triangles in the other faces which contain them:
Two different pictures appear in ( also present the first one). The first presents the upper and lower pyramids of the above octahedron and asserts that given a lower pyramid, we can fill in an upper pyramid so that the two paths from Y to Y′, and from Y′ to Y, are equal (this condition is omitted, perhaps erroneously, from Hartshorne's presentation). The triangles marked + are commutative and those marked "d" are distinguished:
The second diagram is a more innovative presentation. Distinguished triangles are presented linearly, and the diagram emphasizes the fact that the four triangles in the "octahedron" are connected by a series of maps of triangles, where three triangles (namely, those completing the morphisms from X to Y, from Y to Z, and from X to Z) are given and the existence of the fourth is claimed. We pass between the first two by "pivoting" about X, to the third by pivoting about Z, and to the fourth by pivoting about X′. All enclosures in this diagram are commutative (both trigons and the square) but the other commutative square, expressing the equality of the two paths from Y′ to Y, is not evident. All the arrows pointing "off the edge" are degree 1:
This last diagram also illustrates a useful intuitive interpretation of the octahedral axiom. Since in triangulated categories, triangles play the role of exact sequences, we can pretend that

in which case the existence of the last triangle expresses on the one hand (looking at the triangle
(looking at the triangle  ), and
), and (looking at the triangle
(looking at the triangle  ).
).
Putting these together, the octahedral axiom asserts the "third isomorphism theorem":
When the triangulated category is K(A) for some abelian category A, and when X, Y, Z are objects of A placed in degree 0 in their eponymous complexes, and when the maps are injections in A, then the cones are literally the above quotients, and the pretense becomes truth.
are injections in A, then the cones are literally the above quotients, and the pretense becomes truth.
Finally, gives a way of expressing the octahedral axiom using a two dimensional commutative diagram with 4 rows and 4 columns. also give generalizations of the octahedral axiom.
ially on the morphism (note the non-uniqueness in axiom (TR 3), for example). This non-uniqueness is a potential source of errors, among other things preventing in many cases a triangulated category from being the derived category of its core (with respect to a particular t-structure). The axioms do however seem to work adequately in practice, and there is currently no convincing replacement. A few proposals have been developed, however, such as derivator
s that Grothendieck has developed in his long, unfinished and unpublished manuscript from 1991.
A is a cohomological functor if for every distinguished triangle
which can be written as the doubly infinite sequence of morphisms
the following sequence (obtained by applying F to this one) is a long exact sequence:
In a general triangulated category we are guaranteed that the functors

for any object A, are cohomological, with values in the category of abelian group
s (the latter is a contravariant functor, which we view as taking values in the opposite category
, also abelian). That is, we have for example an exact sequence (for the above triangle)
The functors are also written
in analogy with the Ext functor
s in derived categories. Thus we have the familiar sequence
A distinguished triangle is a sequence which is
which is
exact
at X, Y and Z.
2. If A is an abelian category, then the homotopy category
K(A) has as objects all complexes of objects of A, and as morphisms the homotopy classes of morphisms of complexes. Then K(A) is a triangulated category; the distinguished triangles consist of triangles isomorphic to a morphism with its mapping cone
(in the sense of chain complexes). It is possible to create variations, using complexes that are bounded on the left, or on the right, or on both sides.
3. The derived category
of A is also a triangulated category; it is created from
K(A) by localizing at the class of quasi-isomorphisms, a process we now describe.
Under some reasonable conditions on the localizing set S, a localization of a triangulated category is also triangulated. In particular, these conditions are:
S is then said to be "compatible with the triangulation". It is not hard to see that this is the case when S is the class of quasi-isomorphisms in K(A), so in particular the derived category
of A, which is the localization
of K(A) with respect to quasi-isomorphism
s, is triangulated.
4. The topologist's stable homotopy category is another example of a triangulated category.
The objects are spectra
, the suspension is the translation
functor, and the cofibration sequences are the distinguished triangles.
A partial solution to this problem, is to impose a t-structure on the triangulated category D. Different t-structures on D will give rise to different abelian categories inside it. This notion was presented in .
The prototype is the t-structure on the derived category D of an abelian category A.
For each n there are natural full subcategories and
and  consisting of complexes whose cohomology is "bounded below" or "bounded above" n, respectively. Since for any complex X, we have
consisting of complexes whose cohomology is "bounded below" or "bounded above" n, respectively. Since for any complex X, we have  , these are related to each other:
, these are related to each other:
These subcategories also have the following properties:
A t-structure on a triangulated category consists of full subcategories and
and  satisfying the conditions above. In Faisceaux pervers
satisfying the conditions above. In Faisceaux pervers
a triangulated category equipped with a t-structure is called a t-category.
The core or heart (the original French word is "coeur") of a t-structure is the category . It is an abelian category, whereas a triangulated category is additive but almost never abelian. The core of a t-structure on the derived category of A can be thought of as a sort of twisted version of A, which sometimes has better properties. For example, the category of perverse sheaves is the core of a certain (quite complicated) t-structure on the derived category of the category of sheaves. Over a space with singularities, the category of perverse sheaves is similar to the category of sheaves but behaves better
. It is an abelian category, whereas a triangulated category is additive but almost never abelian. The core of a t-structure on the derived category of A can be thought of as a sort of twisted version of A, which sometimes has better properties. For example, the category of perverse sheaves is the core of a certain (quite complicated) t-structure on the derived category of the category of sheaves. Over a space with singularities, the category of perverse sheaves is similar to the category of sheaves but behaves better
.
A basic example of a t-structure is the "natural" one on the derived category
D of some abelian category, where are the full subcategories of complexes whose cohomologies vanish in degrees less than or greater than 0. This t-structure has the following features:
are the full subcategories of complexes whose cohomologies vanish in degrees less than or greater than 0. This t-structure has the following features:
These properties carry over without change to any t-structure, in that if D is a t-category, then there exist truncation functors into its core, from which we obtain a cohomology functor taking values in the core, and the above properties are satisfied for both.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
category
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
satisfying some axiom
Axiom
In traditional logic, an axiom or postulate is a proposition that is not proven or demonstrated but considered either to be self-evident or to define and delimit the realm of analysis. In other words, an axiom is a logical statement that is assumed to be true...
s that are based on the properties of the homotopy category of spectra
Spectrum (homotopy theory)
In algebraic topology, a branch of mathematics, a spectrum is an object representing a generalized cohomology theory. There are several different constructions of categories of spectra, any of which gives a context for the same stable homotopy theory....
, and the derived category
Derived category
In mathematics, the derived category D of an abelian category C is a construction of homological algebra introduced to refine and in a certain sense to simplify the theory of derived functors defined on C...
of an abelian category
Abelian category
In mathematics, an abelian category is a category in which morphisms and objects can be added and in which kernels and cokernels exist and have desirable properties. The motivating prototype example of an abelian category is the category of abelian groups, Ab. The theory originated in a tentative...
. A t-category is a triangulated category with a t-structure.
History
The notion of a derived category was introduced by in his Ph.D. thesis, based on the ideas of Grothendieck. He also defined the notion of a triangulated category, based upon the observation that a derived category had some special "triangles", by writing down axioms for the basic properties of these triangles. A very similar set of axioms was written down at about the same time by .Definition
A translation functor on a category D is an automorphism (or for some authors, an auto-equivalence) T from D to D. One usually uses the notation
and likewise for morphisms from X to Y.
A triangle (X, Y, Z, u, v, w) is a set of 3 objects X, Y, and Z, together with morphisms u from X to Y, v from Y to Z and w from Z to X[1]. Triangles are generally written in the unravelled form:

There are two ways to rotate the above triangle:
 or
or 
A triangulated category is an additive categoryAdditive categoryIn mathematics, specifically in category theory, an additive category is a preadditive category C such that all finite collections of objects A1,...,An of C have a biproduct A1 ⊕ ⋯ ⊕ An in C....
D with a
translation functor and a class of triangles, called distinguished triangles, satisfying the following properties:
- (TR 1) Every triangulated category contains the following triangles:
- For any object X, the following triangle is distinguished:
- For any morphism from X to Y, there is an object Z (called a mapping cone of the morphism) fitting into a distinguished triangle
- Any triangle isomorphic to a distinguished triangle is distinguished.
- For any object X, the following triangle is distinguished:
- (TR 2) The rotations of any distinguished triangle are distinguished.
- (TR 3) Given a map between two morphisms, there is a morphism between their mapping cones (which exist by axiom (TR 1)), that makes everything commuteCommutative diagramIn mathematics, and especially in category theory, a commutative diagram is a diagram of objects and morphisms such that all directed paths in the diagram with the same start and endpoints lead to the same result by composition...
. This means that in the following diagram (where f and g form the map of morphisms) there exists some map h (not necessarily unique) making all the squares commute: - (TR 4) This is called the octahedral axiom. Suppose we have morphisms from X to Y and Y to Z, so that we also have a composed morphism from X to Z. Form distinguished triangles for each of these three morphisms. The octahedral axiom states (roughly) that the three mapping cones can be made into the vertices of a distinguished triangle so that "everything commutes".
These axioms are not entirely independent, since (TR 3) can be derived from the others.
The octahedral axiom
The final axiom (TR 4) is called the "octahedral axiom" because drawing all the objects and morphisms gives the skeleton of an octahedron, four of whose faces are distinguished triangles. There seems to be no really satisfactory way to draw everything in two dimensions; see for details. The presentation here is Verdier's own, and appears, complete with octahedral diagram, in . In the following diagram, u and v are the given morphisms, and the primed letters are the cones of various maps (chosen so that every distinguished triangle has an X, a Y, and a Z letter). Various arrows have been marked with to indicate that they are of "degree 1"; e.g. the map from Z′ to X is in fact from Z′ to T(X). The octahedral axiom then asserts the existence of maps f and g forming a distinguished triangle, and so that f and g form commutative triangles in the other faces which contain them:
to indicate that they are of "degree 1"; e.g. the map from Z′ to X is in fact from Z′ to T(X). The octahedral axiom then asserts the existence of maps f and g forming a distinguished triangle, and so that f and g form commutative triangles in the other faces which contain them:
Two different pictures appear in ( also present the first one). The first presents the upper and lower pyramids of the above octahedron and asserts that given a lower pyramid, we can fill in an upper pyramid so that the two paths from Y to Y′, and from Y′ to Y, are equal (this condition is omitted, perhaps erroneously, from Hartshorne's presentation). The triangles marked + are commutative and those marked "d" are distinguished:
The second diagram is a more innovative presentation. Distinguished triangles are presented linearly, and the diagram emphasizes the fact that the four triangles in the "octahedron" are connected by a series of maps of triangles, where three triangles (namely, those completing the morphisms from X to Y, from Y to Z, and from X to Z) are given and the existence of the fourth is claimed. We pass between the first two by "pivoting" about X, to the third by pivoting about Z, and to the fourth by pivoting about X′. All enclosures in this diagram are commutative (both trigons and the square) but the other commutative square, expressing the equality of the two paths from Y′ to Y, is not evident. All the arrows pointing "off the edge" are degree 1:
This last diagram also illustrates a useful intuitive interpretation of the octahedral axiom. Since in triangulated categories, triangles play the role of exact sequences, we can pretend that

in which case the existence of the last triangle expresses on the one hand
 (looking at the triangle
(looking at the triangle  ), and
), and (looking at the triangle
(looking at the triangle  ).
).Putting these together, the octahedral axiom asserts the "third isomorphism theorem":

When the triangulated category is K(A) for some abelian category A, and when X, Y, Z are objects of A placed in degree 0 in their eponymous complexes, and when the maps
 are injections in A, then the cones are literally the above quotients, and the pretense becomes truth.
are injections in A, then the cones are literally the above quotients, and the pretense becomes truth.Finally, gives a way of expressing the octahedral axiom using a two dimensional commutative diagram with 4 rows and 4 columns. also give generalizations of the octahedral axiom.
Are there better axioms?
These axioms seem rather artificial. It is strongly suspected by experts (see, for example) that triangulated categories are not really the "correct" concept. The essential reason is that the mapping cone of a morphism is unique only up to a non-unique isomorphism. In particular the mapping cone of a morphism does not in general depend functorFunctor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
ially on the morphism (note the non-uniqueness in axiom (TR 3), for example). This non-uniqueness is a potential source of errors, among other things preventing in many cases a triangulated category from being the derived category of its core (with respect to a particular t-structure). The axioms do however seem to work adequately in practice, and there is currently no convincing replacement. A few proposals have been developed, however, such as derivator
Derivator
In mathematics, derivators are a proposed new framework for homological algebra and various generalisations. It is intended to address the perceived deficiencies of derived categories and provide at the same time a language for homotopical algebra....
s that Grothendieck has developed in his long, unfinished and unpublished manuscript from 1991.
Cohomology in triangulated categories
Triangulated categories admit a notion of cohomology and every triangulated category includes a large number of cohomological functors. By definition, a functor F from a triangulated category D into an abelian categoryAbelian category
In mathematics, an abelian category is a category in which morphisms and objects can be added and in which kernels and cokernels exist and have desirable properties. The motivating prototype example of an abelian category is the category of abelian groups, Ab. The theory originated in a tentative...
A is a cohomological functor if for every distinguished triangle

which can be written as the doubly infinite sequence of morphisms

the following sequence (obtained by applying F to this one) is a long exact sequence:

In a general triangulated category we are guaranteed that the functors

for any object A, are cohomological, with values in the category of abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
s (the latter is a contravariant functor, which we view as taking values in the opposite category
Opposite category
In category theory, a branch of mathematics, the opposite category or dual category Cop of a given category C is formed by reversing the morphisms, i.e. interchanging the source and target of each morphism. Doing the reversal twice yields the original category, so the opposite of an opposite...
, also abelian). That is, we have for example an exact sequence (for the above triangle)

The functors are also written

in analogy with the Ext functor
Ext functor
In mathematics, the Ext functors of homological algebra are derived functors of Hom functors. They were first used in algebraic topology, but are common in many areas of mathematics.- Definition and computation :...
s in derived categories. Thus we have the familiar sequence

Examples
1. Vector spaces (over a field) form an elementary triangulated category in which X[1]=X for all X.A distinguished triangle is a sequence
 which is
which isexact
Exact sequence
An exact sequence is a concept in mathematics, especially in homological algebra and other applications of abelian category theory, as well as in differential geometry and group theory...
at X, Y and Z.
2. If A is an abelian category, then the homotopy category
Homotopy category of chain complexes
In homological algebra in mathematics, the homotopy category K of chain complexes in an additive category A is a framework for working with chain homotopies and homotopy equivalences...
K(A) has as objects all complexes of objects of A, and as morphisms the homotopy classes of morphisms of complexes. Then K(A) is a triangulated category; the distinguished triangles consist of triangles isomorphic to a morphism with its mapping cone
Mapping cone (homological algebra)
In homological algebra, the mapping cone is a construction on a map of chain complexes inspired by the analogous construction in topology. In the theory of triangulated categories it is a kind of combined kernel and cokernel: if the chain complexes take their terms in an abelian category, so that...
(in the sense of chain complexes). It is possible to create variations, using complexes that are bounded on the left, or on the right, or on both sides.
3. The derived category
Derived category
In mathematics, the derived category D of an abelian category C is a construction of homological algebra introduced to refine and in a certain sense to simplify the theory of derived functors defined on C...
of A is also a triangulated category; it is created from
K(A) by localizing at the class of quasi-isomorphisms, a process we now describe.
Under some reasonable conditions on the localizing set S, a localization of a triangulated category is also triangulated. In particular, these conditions are:
- S is closed under all translations, and
- For any two triangles

 and arrows
and arrows  as in the axioms, if these arrows are both in S then the promised arrow
as in the axioms, if these arrows are both in S then the promised arrow  completing the map of triangles is also in S.
completing the map of triangles is also in S.
S is then said to be "compatible with the triangulation". It is not hard to see that this is the case when S is the class of quasi-isomorphisms in K(A), so in particular the derived category
Derived category
In mathematics, the derived category D of an abelian category C is a construction of homological algebra introduced to refine and in a certain sense to simplify the theory of derived functors defined on C...
of A, which is the localization
Localization of a category
In mathematics, localization of a category consists of adding to a category inverse morphisms for some collection of morphisms, constraining them to become isomorphisms. This is formally similar to the process of localization of a ring; it in general makes objects isomorphic that were not so before...
of K(A) with respect to quasi-isomorphism
Quasi-isomorphism
In homological algebra, a branch of mathematics, a quasi-isomorphism is a morphism A → B of chain complexes such that the induced morphisms...
s, is triangulated.
4. The topologist's stable homotopy category is another example of a triangulated category.
The objects are spectra
Spectrum (homotopy theory)
In algebraic topology, a branch of mathematics, a spectrum is an object representing a generalized cohomology theory. There are several different constructions of categories of spectra, any of which gives a context for the same stable homotopy theory....
, the suspension is the translation
functor, and the cofibration sequences are the distinguished triangles.
t-structures
Verdier introduced triangulated categories in order to place derived categories in a category-theoretic context: for every abelian category A there exists a triangulated category D(A), containing A as a full subcategory (the "0-complexes" concentrated in cohomological degree 0), and in which we can construct derived functors. Unfortunately, different abelian categories can give rise to equivalent derived categories, so that it is impossible to reconstruct A from the triangulated category D(A).A partial solution to this problem, is to impose a t-structure on the triangulated category D. Different t-structures on D will give rise to different abelian categories inside it. This notion was presented in .
The prototype is the t-structure on the derived category D of an abelian category A.
For each n there are natural full subcategories
 and
and  consisting of complexes whose cohomology is "bounded below" or "bounded above" n, respectively. Since for any complex X, we have
consisting of complexes whose cohomology is "bounded below" or "bounded above" n, respectively. Since for any complex X, we have  , these are related to each other:
, these are related to each other:
These subcategories also have the following properties:
 ,
, 

- Every object Y can be embedded in a distinguished triangle
 with
with  ,
, 
A t-structure on a triangulated category consists of full subcategories
 and
and  satisfying the conditions above. In Faisceaux pervers
satisfying the conditions above. In Faisceaux perversa triangulated category equipped with a t-structure is called a t-category.
The core or heart (the original French word is "coeur") of a t-structure is the category
 . It is an abelian category, whereas a triangulated category is additive but almost never abelian. The core of a t-structure on the derived category of A can be thought of as a sort of twisted version of A, which sometimes has better properties. For example, the category of perverse sheaves is the core of a certain (quite complicated) t-structure on the derived category of the category of sheaves. Over a space with singularities, the category of perverse sheaves is similar to the category of sheaves but behaves better
. It is an abelian category, whereas a triangulated category is additive but almost never abelian. The core of a t-structure on the derived category of A can be thought of as a sort of twisted version of A, which sometimes has better properties. For example, the category of perverse sheaves is the core of a certain (quite complicated) t-structure on the derived category of the category of sheaves. Over a space with singularities, the category of perverse sheaves is similar to the category of sheaves but behaves betterWell-behaved
Mathematicians very frequently speak of whether a mathematical object — a function, a set, a space of one sort or another — is "well-behaved" or not. The term has no fixed formal definition, and is dependent on mathematical interests, fashion, and taste...
.
A basic example of a t-structure is the "natural" one on the derived category
Derived category
In mathematics, the derived category D of an abelian category C is a construction of homological algebra introduced to refine and in a certain sense to simplify the theory of derived functors defined on C...
D of some abelian category, where
 are the full subcategories of complexes whose cohomologies vanish in degrees less than or greater than 0. This t-structure has the following features:
are the full subcategories of complexes whose cohomologies vanish in degrees less than or greater than 0. This t-structure has the following features:- The truncation functors
 , or in fact
, or in fact  for any n, which are obtained by translating the argument of the original two functors. Abstractly, these are the left adjoint and right adjoint, respectively, to the inclusion functors of
for any n, which are obtained by translating the argument of the original two functors. Abstractly, these are the left adjoint and right adjoint, respectively, to the inclusion functors of  in D. In addition, the truncation functors fit into a triangle, and this is in fact the unique triangle satisfying the third axiom above:
in D. In addition, the truncation functors fit into a triangle, and this is in fact the unique triangle satisfying the third axiom above:
- The cohomology functor
 , or in fact
, or in fact  , which is obtained by translating its argument:
, which is obtained by translating its argument:  . Its relationship to the truncation functors is that they are defined so that for any complex A,
. Its relationship to the truncation functors is that they are defined so that for any complex A,  for
for  and is unchanged for
and is unchanged for  ; likewise for
; likewise for  ; in particular,
; in particular,  is not independent of them, but in fact
is not independent of them, but in fact  . Furthermore, the cohomology is a cohomological functor: for any triangle
. Furthermore, the cohomology is a cohomological functor: for any triangle  we obtain a long exact sequence
we obtain a long exact sequence
These properties carry over without change to any t-structure, in that if D is a t-category, then there exist truncation functors into its core, from which we obtain a cohomology functor taking values in the core, and the above properties are satisfied for both.




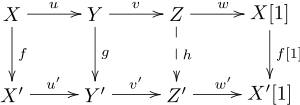
.svg.png)
.svg.png)
.svg.png)