
Opposite category
Encyclopedia
In category theory
, a branch of mathematics
, the opposite category or dual category Cop of a given category C is formed by reversing the morphism
s, i.e. interchanging the source and target of each morphism. Doing the reversal twice yields the original category, so the opposite of an opposite category is the original category itself. In symbols, .
.
 (see product category
(see product category
)
 (see functor category
(see functor category
)
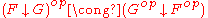 (see comma category
(see comma category
)
Citations
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
, a branch of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the opposite category or dual category Cop of a given category C is formed by reversing the morphism
Morphism
In mathematics, a morphism is an abstraction derived from structure-preserving mappings between two mathematical structures. The notion of morphism recurs in much of contemporary mathematics...
s, i.e. interchanging the source and target of each morphism. Doing the reversal twice yields the original category, so the opposite of an opposite category is the original category itself. In symbols,
 .
.Examples
- An example comes from reversing the direction of inequalities in a partial order. So if X is a set and ≤ a partial order relation, we can define a new partial order relation ≤new by
-
- x ≤new y if and only if y ≤ x.
- For example, there are opposite pairs child/parent, or descendant/ancestor.
- The category of Boolean algebras and Boolean homomorphismHomomorphismIn abstract algebra, a homomorphism is a structure-preserving map between two algebraic structures . The word homomorphism comes from the Greek language: ὁμός meaning "same" and μορφή meaning "shape".- Definition :The definition of homomorphism depends on the type of algebraic structure under...
s is equivalentEquivalence of categoriesIn category theory, an abstract branch of mathematics, an equivalence of categories is a relation between two categories that establishes that these categories are "essentially the same". There are numerous examples of categorical equivalences from many areas of mathematics...
to the opposite of the category of Stone spaces and continuous functions.
- The category of affine schemes is equivalent to the opposite of the category of commutative ringCommutative ringIn ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
s.
- The Pontryagin dualityPontryagin dualityIn mathematics, specifically in harmonic analysis and the theory of topological groups, Pontryagin duality explains the general properties of the Fourier transform on locally compact groups, such as R, the circle or finite cyclic groups.-Introduction:...
restricts to an equivalence between the category of compact HausdorffHausdorff spaceIn topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
abelianAbelian groupIn abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
topological groupTopological groupIn mathematics, a topological group is a group G together with a topology on G such that the group's binary operation and the group's inverse function are continuous functions with respect to the topology. A topological group is a mathematical object with both an algebraic structure and a...
s and the opposite of the category of (discrete) abelian groups.
- By the Gelfand-Neumark theorem, the category of localizable measurable spacesSigma-algebraIn mathematics, a σ-algebra is a technical concept for a collection of sets satisfying certain properties. The main use of σ-algebras is in the definition of measures; specifically, the collection of sets over which a measure is defined is a σ-algebra...
(with measurable mapsMeasurable functionIn mathematics, particularly in measure theory, measurable functions are structure-preserving functions between measurable spaces; as such, they form a natural context for the theory of integration...
) is equivalent to the category of commutative Von Neumann algebrasVon Neumann algebraIn mathematics, a von Neumann algebra or W*-algebra is a *-algebra of bounded operators on a Hilbert space that is closed in the weak operator topology and contains the identity operator. They were originally introduced by John von Neumann, motivated by his study of single operators, group...
(with normalNormal operatorIn mathematics, especially functional analysis, a normal operator on a complex Hilbert space H is a continuous linear operatorN:H\to Hthat commutes with its hermitian adjoint N*: N\,N^*=N^*N....
unitalUnital mapIn abstract algebra, a unital map on a C*-algebra is a map \phi which preserves the identity element:\phi = I. \, This condition appears often in the context of completely positive maps, especially when they represent quantum operations....
homomorphisms of *-algebras).
Properties
 (see product category
(see product categoryProduct category
In the mathematical field of category theory, the product of two categories C and D, denoted and called a product category, is a straightforward extension of the concept of the Cartesian product of two sets.-Definition:...
)
 (see functor category
(see functor categoryFunctor category
In category theory, a branch of mathematics, the functors between two given categories form a category, where the objects are the functors and the morphisms are natural transformations between the functors...
)
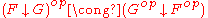 (see comma category
(see comma categoryComma category
In mathematics, a comma category is a construction in category theory. It provides another way of looking at morphisms: instead of simply relating objects of a category to one another, morphisms become objects in their own right. This notion was introduced in 1963 by F. W...
)
See also
- Dual objectDual objectIn category theory, a branch of mathematics, it is possible to define a concept of dual object generalizing the concept of dual space in linear algebra.A category in which each object has a dual is called autonomous or rigid.-Definition:...
- Dual (category theory)Dual (category theory)In category theory, a branch of mathematics, duality is a correspondence between properties of a category C and so-called dual properties of the opposite category Cop...
- Duality (mathematics)Duality (mathematics)In mathematics, a duality, generally speaking, translates concepts, theorems or mathematical structures into other concepts, theorems or structures, in a one-to-one fashion, often by means of an involution operation: if the dual of A is B, then the dual of B is A. As involutions sometimes have...
- Contravariant functor
- Opposite functor
Citations

