Dual object
Encyclopedia
In category theory
, a branch of mathematics
, it is possible to define a concept of dual object generalizing the concept of dual space
in linear algebra
.
A category in which each object has a dual is called autonomous or rigid.
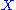in a monoidal category
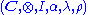. The object 
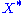is called a left dual of 
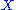if there exist two morphsims
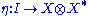, called the coevaluation, and 
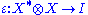, called the evaluation,
satisfying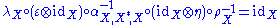
and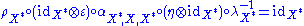
.
The object
is called the right dual of 
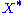. Left duals are canonically isomorphic when they exist, as are right duals. When C is braided (or symmetric), every left dual is also a right dual, and vice versa.
If we consider a monoidal category as a bicategory
with one object, a dual pair is exactly an adjoint pair.
. A monoidal category where every object has both a left and a right dual is called an autonomous category
. An autonomous category that is also symmetric is called a compact closed category
.
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
, a branch of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, it is possible to define a concept of dual object generalizing the concept of dual space
Dual space
In mathematics, any vector space, V, has a corresponding dual vector space consisting of all linear functionals on V. Dual vector spaces defined on finite-dimensional vector spaces can be used for defining tensors which are studied in tensor algebra...
in linear algebra
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
.
A category in which each object has a dual is called autonomous or rigid.
Definition
Consider an object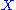 in a monoidal categoryMonoidal category
In mathematics, a monoidal category is a category C equipped with a bifunctorwhich is associative, up to a natural isomorphism, and an object I which is both a left and right identity for ⊗, again up to a natural isomorphism...
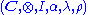. The object 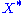is called a left dual of 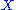if there exist two morphsims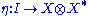, called the coevaluation, and 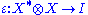, called the evaluation,satisfying
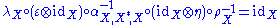
and
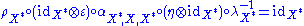.The object
is called the right dual of 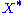. Left duals are canonically isomorphic when they exist, as are right duals. When C is braided (or symmetric), every left dual is also a right dual, and vice versa.If we consider a monoidal category as a bicategory
Bicategory
In mathematics, a bicategory is a concept in category theory used to extend the notion of category to handle the cases where the composition of morphisms is not associative, but only associative up to an isomorphism. The notion was introduced in 1967 by Jean Bénabou.Formally, a bicategory B...
with one object, a dual pair is exactly an adjoint pair.
Categories with duals
A monoidal category where every object has a left (resp. right) dual is sometimes called a left (resp. right) autonomous category. Algebraic geometers call it a left (resp. right) rigid categoryRigid category
In category theory, a branch of mathematics, a rigid category is a monoidal category where every object is rigid, that is, has a dual X* and a morphism 1 → X ⊗ X* satisfying natural conditions. The category is called right rigid or left rigid according to whether it has right duals or...
. A monoidal category where every object has both a left and a right dual is called an autonomous category
Autonomous category
In mathematics, an autonomous category is a monoidal category where dual objects exist.-Definition:A left autonomous category is a monoidal category where every object has a left dual. An autonomous category is a monoidal category where every object has both a left and a right dual...
. An autonomous category that is also symmetric is called a compact closed category
Compact closed category
In category theory, compact closed categories are a general context for treating dual objects. The idea of a dual object generalizes the more familiar concept of the dual of a finite-dimensional vector space...
.