Spectrum (homotopy theory)
Encyclopedia
In algebraic topology
, a branch of mathematics
, a spectrum is an object representing a generalized cohomology theory. There are several different constructions of categories of spectra, any of which gives a context for the same stable homotopy theory
.
A spectrum is a sequence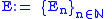
of CW complexes together with inclusions 
of the suspension 
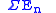as a subcomplex of 
.
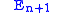A function between two spectra E and F is a sequence of maps from En to Fn that commute with the
maps ΣEn→En+1 and ΣFn→Fn+1.
Given a spectrum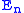
, a subspectrum 
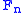is a sequence of subcomplexes that is also a spectrum. As each i-cell in 
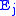suspends to an (i+1)-cell in 
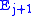, a cofinal subspectrum is a subspectrum for which each cell of the parent spectrum is eventually contained in the subspectrum after a finite number of suspensions. Spectra can then be turned into a category by defining a map of spectra 
to be a function from a cofinal subspectrum 
of 
to F, where two such functions represent the same map if they coincide on some cofinal subspectrum. Intuitively such a map of spectra does not need to be everywhere defined, just eventually become defined, and two maps that coincide on a cofinal subspectrum are said to be equivalent.
This gives the category of spectra (and maps), which is a major tool. There is a natural embedding of the category of pointed CW complexes into this category: it takes
to the suspension spectrum in which the nth complex is 
.
The smash product
of a spectrum
and a pointed complex 
is a spectrum given by 
(associativity of the smash product yields immediately that this is indeed a spectrum). A homotopy of maps between spectra corresponds to a map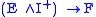 
, where 
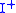is the disjoint union 
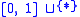with * taken to be the basepoint.
The stable homotopy category, or homotopy category of (CW) spectra is defined to be the category whose objects are spectra and whose morphisms are homotopy classes of maps between spectra. Many other definitions of spectrum, some appearing very different, lead to equivalent stable homotopy categories.
Finally, we can define the suspension of a spectrum by
. This translation suspension is invertible, as we can desuspend too, by setting
.
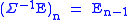(Vogt (1970)), the shift being given by suspension and the distinguished triangles by the mapping cone
sequences of spectra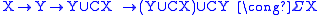
.
The smash product is compatible with the triangulated category structure. In particular the smash product of a distinguished triangle with a spectrum is a distinguished triangle.
,
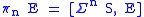where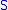
is the spectrum of spheres and 
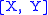is the set of homotopy classes of maps from 
to 
.
We define the generalized homology theory of a spectrum E by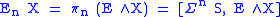
and define its generalized cohomology theory by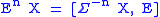
.
Here
can be a spectrum or a (by using its suspension spectrum) a space.
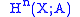with coefficients in an abelian group
A. By Brown representability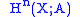
is the set of homotopy classes of maps from X to K(A,n), the Eilenberg-MacLane space
with homotopy concentrated in degree n. Then the corresponding spectrum HA has n'th space K(A,n); it is called the Eilenberg-MacLane spectrum.
As a second important example, consider topological K-theory
. At least for X compact,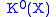
is defined to be the Grothendieck group
of the monoid
of complex vector bundles on X. Also,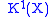
is the group corresponding to vector bundles on the suspension of X. Topological K-theory is a generalized cohomology theory, so it gives a spectrum. The zero'th space is 
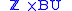while the first space is 
. Here 
is the infinite unitary group
and
is its classifying space
. By Bott periodicity we get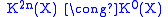
and 
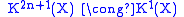for all n, so all the spaces in the topological K-theory spectrum are given by either 
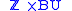or 
. There is a corresponding construction using real vector bundles instead of complex vector bundles, which gives an 8-periodic spectrum.
For many more examples, see the list of cohomology theories.
wrote further on the subject in 1959. Spectra were adopted by Michael Atiyah
and George W. Whitehead
in their work on generalized homology theories in the early 1960s. The 1964 doctoral thesis of J. Michael Boardman
gave a workable definition of a category of spectra and of maps (not just homotopy classes) between them, as useful in stable homotopy theory as the category of CW complex
es is in the unstable case. (This is essentially the category described above, and it is still used for many purposes: for other accounts, see Adams
(1974) or Vogt (1970).) Important further theoretical advances have however been made since 1990, improving vastly the formal properties of spectra. Consequently, much recent literature uses modified definitions of spectrum: see Mandell et al. (2001) for a unified treatment of these new approaches.
Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
, a branch of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a spectrum is an object representing a generalized cohomology theory. There are several different constructions of categories of spectra, any of which gives a context for the same stable homotopy theory
Stable homotopy theory
In mathematics, stable homotopy theory is that part of homotopy theory concerned with all structure and phenomena that remain after sufficiently many applications of the suspension functor...
.
The definition of a spectrum
There are many variations of the definition: the treatment here is close to that in Adams (1974).A spectrum is a sequence
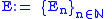of CW complexes together with inclusions of the suspension 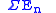as a subcomplex of 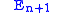.Functions, maps, and homotopies of spectra
There are three natural categories whose objects are spectra, whose morphisms are the functions, or maps, or homotopy classes defined below.A function between two spectra E and F is a sequence of maps from En to Fn that commute with the
maps ΣEn→En+1 and ΣFn→Fn+1.
Given a spectrum
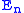, a subspectrum 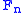is a sequence of subcomplexes that is also a spectrum. As each i-cell in 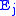suspends to an (i+1)-cell in 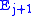, a cofinal subspectrum is a subspectrum for which each cell of the parent spectrum is eventually contained in the subspectrum after a finite number of suspensions. Spectra can then be turned into a category by defining a map of spectra to be a function from a cofinal subspectrum of to F, where two such functions represent the same map if they coincide on some cofinal subspectrum. Intuitively such a map of spectra does not need to be everywhere defined, just eventually become defined, and two maps that coincide on a cofinal subspectrum are said to be equivalent.This gives the category of spectra (and maps), which is a major tool. There is a natural embedding of the category of pointed CW complexes into this category: it takes
to the suspension spectrum in which the nth complex is .The smash product
Smash product
In mathematics, the smash product of two pointed spaces X and Y is the quotient of the product space X × Y under the identifications ∼ for all x ∈ X and y ∈ Y. The smash product is usually denoted X ∧ Y...
of a spectrum
and a pointed complex is a spectrum given by (associativity of the smash product yields immediately that this is indeed a spectrum). A homotopy of maps between spectra corresponds to a map 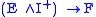, where 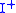is the disjoint union 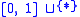with * taken to be the basepoint.The stable homotopy category, or homotopy category of (CW) spectra is defined to be the category whose objects are spectra and whose morphisms are homotopy classes of maps between spectra. Many other definitions of spectrum, some appearing very different, lead to equivalent stable homotopy categories.
Finally, we can define the suspension of a spectrum by
. This translation suspension is invertible, as we can desuspend too, by setting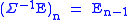.The triangulated homotopy category of spectra
The stable homotopy category is additive: maps can be added by using a variant of the track addition used to define homotopy groups. Thus homotopy classes from one spectrum to another form an abelian group. Furthermore the stable homotopy category is triangulatedTriangulated category
A triangulated category is a mathematical category satisfying some axioms that are based on the properties of the homotopy category of spectra, and the derived category of an abelian category. A t-category is a triangulated category with a t-structure.- History :The notion of a derived category...
(Vogt (1970)), the shift being given by suspension and the distinguished triangles by the mapping cone
Mapping cone
In mathematics, especially homotopy theory, the mapping cone is a construction C_f of topology, analogous to a quotient space. It is also called the homotopy cofiber, and also notated Cf.-Definition:...
sequences of spectra
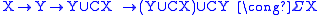.Smash products of spectra
The smash product of spectra extends the smash product of CW complexes. It is somewhat cumbersome to define. It makes the stable homotopy category into a monoidal category; in other words it behaves like the tensor product of abelian groups. A major problem with the smash product is that obvious ways of defining it make it associative and commutative only up to homotopy. Some more recent definitions of spectra eliminate this problem, and give a symmetric monoidal structure at the level of maps, before passing to homotopy classes.The smash product is compatible with the triangulated category structure. In particular the smash product of a distinguished triangle with a spectrum is a distinguished triangle.
Generalized homology and cohomology of spectra
We can define the (stable) homotopy groups of a spectrum to be those given by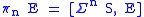,where
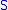is the spectrum of spheres and 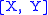is the set of homotopy classes of maps from to .We define the generalized homology theory of a spectrum E by
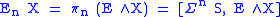
and define its generalized cohomology theory by
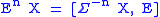.Here
can be a spectrum or a (by using its suspension spectrum) a space.Examples
Consider singular cohomology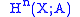 with coefficients in an abelian groupAbelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
A. By Brown representability
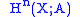is the set of homotopy classes of maps from X to K(A,n), the Eilenberg-MacLane spaceEilenberg-MacLane space
In mathematics, an Eilenberg–MacLane spaceSaunders Mac Lane originally spelt his name "MacLane" , and co-published the papers establishing the notion of Eilenberg–MacLane spaces under this name. In mathematics, an Eilenberg–MacLane spaceSaunders Mac Lane originally spelt his name "MacLane" (without...
with homotopy concentrated in degree n. Then the corresponding spectrum HA has n'th space K(A,n); it is called the Eilenberg-MacLane spectrum.
As a second important example, consider topological K-theory
Topological K-theory
In mathematics, topological K-theory is a branch of algebraic topology. It was founded to study vector bundles on general topological spaces, by means of ideas now recognised as K-theory that were introduced by Alexander Grothendieck...
. At least for X compact,
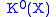is defined to be the Grothendieck groupGrothendieck group
In mathematics, the Grothendieck group construction in abstract algebra constructs an abelian group from a commutative monoid in the best possible way...
of the monoid
Monoid
In abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
of complex vector bundles on X. Also,
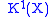is the group corresponding to vector bundles on the suspension of X. Topological K-theory is a generalized cohomology theory, so it gives a spectrum. The zero'th space is 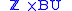while the first space is . Here is the infinite unitary groupUnitary group
In mathematics, the unitary group of degree n, denoted U, is the group of n×n unitary matrices, with the group operation that of matrix multiplication. The unitary group is a subgroup of the general linear group GL...
and
is its classifying spaceClassifying space
In mathematics, specifically in homotopy theory, a classifying space BG of a topological group G is the quotient of a weakly contractible space EG by a free action of G...
. By Bott periodicity we get
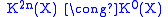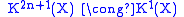and for all n, so all the spaces in the topological K-theory spectrum are given by either 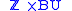or . There is a corresponding construction using real vector bundles instead of complex vector bundles, which gives an 8-periodic spectrum.For many more examples, see the list of cohomology theories.
History
A version of the concept of a spectrum was introduced in the 1958 doctoral dissertation of Elon Lages Lima. His advisor Edwin SpanierEdwin Spanier
Edwin Henry Spanier was an American mathematician at the University of California at Berkeley, working in algebraic topology...
wrote further on the subject in 1959. Spectra were adopted by Michael Atiyah
Michael Atiyah
Sir Michael Francis Atiyah, OM, FRS, FRSE is a British mathematician working in geometry.Atiyah grew up in Sudan and Egypt but spent most of his academic life in the United Kingdom at Oxford and Cambridge, and in the United States at the Institute for Advanced Study...
and George W. Whitehead
George W. Whitehead
George William Whitehead, Jr. was a professor of mathematics at the Massachusetts Institute of Technology, a member of the United States National Academy of Sciences, and a Fellow of the American Academy of Arts and Sciences. He is known for his work on algebraic topology...
in their work on generalized homology theories in the early 1960s. The 1964 doctoral thesis of J. Michael Boardman
Michael Boardman
John Michael Boardman is a mathematician whose speciality is algebraic and differential topology. He was formerly at the University of Cambridge, England; he is currently a full professor at Johns Hopkins University in Baltimore, Maryland USA...
gave a workable definition of a category of spectra and of maps (not just homotopy classes) between them, as useful in stable homotopy theory as the category of CW complex
CW complex
In topology, a CW complex is a type of topological space introduced by J. H. C. Whitehead to meet the needs of homotopy theory. This class of spaces is broader and has some better categorical properties than simplicial complexes, but still retains a combinatorial naturethat allows for...
es is in the unstable case. (This is essentially the category described above, and it is still used for many purposes: for other accounts, see Adams
Frank Adams
John Frank Adams FRS was a British mathematician, one of the founders of homotopy theory.-Life:He was born in Woolwich, a suburb in south-east London. He began research as a student of Abram Besicovitch, but soon switched to algebraic topology. He received his Ph.D. from the University of...
(1974) or Vogt (1970).) Important further theoretical advances have however been made since 1990, improving vastly the formal properties of spectra. Consequently, much recent literature uses modified definitions of spectrum: see Mandell et al. (2001) for a unified treatment of these new approaches.