Eilenberg-MacLane space
Encyclopedia
In mathematics
, an Eilenberg–MacLane spaceSaunders Mac Lane
originally spelt his name "MacLane" (without a space), and co-published the papers establishing the notion of Eilenberg–MacLane spaces under this name. (See e.g. In this context it is therefore conventional to write the name without a space. is a special kind of topological space
that can be regarded as a building block for homotopy theory. These spaces are important in many contexts in algebraic topology
, including constructions of spaces, computations of homotopy group
s of spheres, and definition of cohomology operation
s. The name is for Samuel Eilenberg
and Saunders Mac Lane
, who introduced such spaces in the late 1940s.
Let G be a group and n a positive integer. A connected topological space X is called an Eilenberg–MacLane space of type K(G,n), if it has n-th homotopy group
πn(X) isomorphic to G and all other homotopy groups trivial. If n > 1 then G must be abelian. Then an Eilenberg–MacLane space exists, as a CW-complex, and is unique up to a weak homotopy equivalence. By abuse of language, any such space is often called just K(G,n).
Some further elementary examples can be constructed from these by using the obvious fact that the product K(G,n) × K(H,n) is K(G × H,n).
A K(G,n) can be constructed stage-by-stage, as a CW complex
, starting with a wedge
of n-sphere
s, one for each generator of the group G, and adding cells in (possibly infinite number of) higher dimensions so as to kill all extra homotopy.
of homotopy classes of maps from X to K(G,n) is in natural bijection with the n-th singular cohomology group
of the space X. Thus one says that the K(G,n) are representing spaces for cohomology with coefficients in G. Since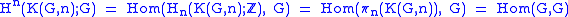
, there is a distinguished element 
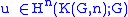corresponding to the identity. The above bijection is given by pullback of that element — 
.
Another version of this result, due to Peter J. Huber, establishes a bijection with the n-th Čech cohomology group
when X is Hausdorff
and paracompact and G is countable, or when X is Hausdorff, paracompact and compactly generated
and G is arbitrary. A further result of Morita establishes a bijection with the n-th numerable Čech cohomology group
for an arbitrary topological space X and G an arbitrary abelian group.
Every CW-complex possesses a Postnikov tower, that is, it is homotopy equivalent to an iterated fibration with fibers the Eilenberg–MacLane spaces.
There is a method due to Jean-Pierre Serre
which allows one, at least theoretically, to compute homotopy groups of spaces using a spectral sequence
for special fibrations with Eilenberg–MacLane spaces for fibers.
The cohomology groups of Eilenberg–MacLane spaces can be used to classify all cohomology operation
s.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, an Eilenberg–MacLane spaceSaunders Mac Lane
Saunders Mac Lane
Saunders Mac Lane was an American mathematician who cofounded category theory with Samuel Eilenberg.-Career:...
originally spelt his name "MacLane" (without a space), and co-published the papers establishing the notion of Eilenberg–MacLane spaces under this name. (See e.g. In this context it is therefore conventional to write the name without a space. is a special kind of topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
that can be regarded as a building block for homotopy theory. These spaces are important in many contexts in algebraic topology
Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
, including constructions of spaces, computations of homotopy group
Homotopy group
In mathematics, homotopy groups are used in algebraic topology to classify topological spaces. The first and simplest homotopy group is the fundamental group, which records information about loops in a space...
s of spheres, and definition of cohomology operation
Cohomology operation
In mathematics, the cohomology operation concept became central to algebraic topology, particularly homotopy theory, from the 1950s onwards, in the shape of the simple definition that if F is a functor defining a cohomology theory, then a cohomology operation should be a natural transformation from...
s. The name is for Samuel Eilenberg
Samuel Eilenberg
Samuel Eilenberg was a Polish and American mathematician of Jewish descent. He was born in Warsaw, Russian Empire and died in New York City, USA, where he had spent much of his career as a professor at Columbia University.He earned his Ph.D. from University of Warsaw in 1936. His thesis advisor...
and Saunders Mac Lane
Saunders Mac Lane
Saunders Mac Lane was an American mathematician who cofounded category theory with Samuel Eilenberg.-Career:...
, who introduced such spaces in the late 1940s.
Let G be a group and n a positive integer. A connected topological space X is called an Eilenberg–MacLane space of type K(G,n), if it has n-th homotopy group
Homotopy group
In mathematics, homotopy groups are used in algebraic topology to classify topological spaces. The first and simplest homotopy group is the fundamental group, which records information about loops in a space...
πn(X) isomorphic to G and all other homotopy groups trivial. If n > 1 then G must be abelian. Then an Eilenberg–MacLane space exists, as a CW-complex, and is unique up to a weak homotopy equivalence. By abuse of language, any such space is often called just K(G,n).
Examples
- The unit circleUnit circleIn mathematics, a unit circle is a circle with a radius of one. Frequently, especially in trigonometry, "the" unit circle is the circle of radius one centered at the origin in the Cartesian coordinate system in the Euclidean plane...
S1 is a K(Z,1). - The infinite-dimensional complex projective spaceComplex projective spaceIn mathematics, complex projective space is the projective space with respect to the field of complex numbers. By analogy, whereas the points of a real projective space label the lines through the origin of a real Euclidean space, the points of a complex projective space label the complex lines...
P∞(C) is a model of K(Z,2). This is one of the rare examples of classifying spaces admitting a manifoldManifoldIn mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
model, and is also the topological spaceTopological spaceTopological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
the homotopy groupHomotopy groupIn mathematics, homotopy groups are used in algebraic topology to classify topological spaces. The first and simplest homotopy group is the fundamental group, which records information about loops in a space...
s of which satisfy πi = 0 for i = 1 and i > 2, while π2 = Z. Its cohomology ringCohomology ringIn mathematics, specifically algebraic topology, the cohomology ring of a topological space X is a ring formed from the cohomology groups of X together with the cup product serving as the ring multiplication. Here 'cohomology' is usually understood as singular cohomology, but the ring structure is...
is Z[x], namely the free polynomial ring on a single 2-dimensional generator x ∈ H2. The generator can be represented in de Rham cohomologyDe Rham cohomologyIn mathematics, de Rham cohomology is a tool belonging both to algebraic topology and to differential topology, capable of expressing basic topological information about smooth manifolds in a form particularly adapted to computation and the concrete representation of cohomology classes...
by the Fubini–Study 2-form. An application of K(Z,2) is described at Abstract nonsenseAbstract nonsenseIn mathematics, abstract nonsense, general abstract nonsense, and general nonsense are terms used facetiously by some mathematicians to describe certain kinds of arguments and methods related to category theory. roughly speaking, category theory is the study of the general form of mathematical...
. - The infinite-dimensional real projective spaceReal projective spaceIn mathematics, real projective space, or RPn, is the topological space of lines through 0 in Rn+1. It is a compact, smooth manifold of dimension n, and a special case of a Grassmannian.-Construction:...
P∞(R) is a K(Z2,1). - The wedge sumWedge sumIn topology, the wedge sum is a "one-point union" of a family of topological spaces. Specifically, if X and Y are pointed spaces the wedge sum of X and Y is the quotient of the disjoint union of X and Y by the identification x0 ∼ y0:X\vee Y = \;/ \sim,\,where ∼ is the...
of k unit circleUnit circleIn mathematics, a unit circle is a circle with a radius of one. Frequently, especially in trigonometry, "the" unit circle is the circle of radius one centered at the origin in the Cartesian coordinate system in the Euclidean plane...
s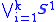
is a K(G,1) for G the free groupFree groupIn mathematics, a group G is called free if there is a subset S of G such that any element of G can be written in one and only one way as a product of finitely many elements of S and their inverses...
on k generators. - The complement to any knot in a 3-dimensional sphere S3 is of type K(G,1); this is called the "asphericityAspherical spaceIn topology, a branch of mathematics, an aspherical space is a topological space with all higher homotopy groups equal to 0.If one works with CW complexes, one can reformulate this condition: an aspherical CW complex is a CW complex whose universal cover is contractible. Indeed, contractibility of...
of knots", and is a 1957 theorem of Christos PapakyriakopoulosChristos PapakyriakopoulosChristos Dimitriou Papakyriakopoulos, commonly known as "Papa" , was a Greek mathematician specializing in geometric topology. He worked in isolation at Athens University being awarded a Ph.D on the recommendation of Carathéodory...
.
Some further elementary examples can be constructed from these by using the obvious fact that the product K(G,n) × K(H,n) is K(G × H,n).
A K(G,n) can be constructed stage-by-stage, as a CW complex
CW complex
In topology, a CW complex is a type of topological space introduced by J. H. C. Whitehead to meet the needs of homotopy theory. This class of spaces is broader and has some better categorical properties than simplicial complexes, but still retains a combinatorial naturethat allows for...
, starting with a wedge
Wedge sum
In topology, the wedge sum is a "one-point union" of a family of topological spaces. Specifically, if X and Y are pointed spaces the wedge sum of X and Y is the quotient of the disjoint union of X and Y by the identification x0 ∼ y0:X\vee Y = \;/ \sim,\,where ∼ is the...
of n-sphere
Sphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
s, one for each generator of the group G, and adding cells in (possibly infinite number of) higher dimensions so as to kill all extra homotopy.
Properties of Eilenberg–MacLane spaces
An important property of K(G,n) is that, for any abelian group G, and any CW-complex X, the set- [X, K(G,n)]
of homotopy classes of maps from X to K(G,n) is in natural bijection with the n-th singular cohomology group
Singular homology
In algebraic topology, a branch of mathematics, singular homology refers to the study of a certain set of algebraic invariants of a topological space X, the so-called homology groups H_n....
- Hn(X; G)
of the space X. Thus one says that the K(G,n) are representing spaces for cohomology with coefficients in G. Since
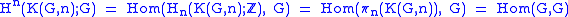, there is a distinguished element 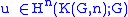corresponding to the identity. The above bijection is given by pullback of that element — .Another version of this result, due to Peter J. Huber, establishes a bijection with the n-th Čech cohomology group
Cech cohomology
In mathematics, specifically algebraic topology, Čech cohomology is a cohomology theory based on the intersection properties of open covers of a topological space. It is named for the mathematician Eduard Čech.-Motivation:...
when X is Hausdorff
Hausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
and paracompact and G is countable, or when X is Hausdorff, paracompact and compactly generated
Compactly generated space
In topology, a compactly generated space is a topological space whose topology is coherent with the family of all compact subspaces. Specifically, a topological space X is compactly generated if it satisfies the following condition:Equivalently, one can replace closed with open in this definition...
and G is arbitrary. A further result of Morita establishes a bijection with the n-th numerable Čech cohomology group
Cech cohomology
In mathematics, specifically algebraic topology, Čech cohomology is a cohomology theory based on the intersection properties of open covers of a topological space. It is named for the mathematician Eduard Čech.-Motivation:...
for an arbitrary topological space X and G an arbitrary abelian group.
Every CW-complex possesses a Postnikov tower, that is, it is homotopy equivalent to an iterated fibration with fibers the Eilenberg–MacLane spaces.
There is a method due to Jean-Pierre Serre
Jean-Pierre Serre
Jean-Pierre Serre is a French mathematician. He has made contributions in the fields of algebraic geometry, number theory, and topology.-Early years:...
which allows one, at least theoretically, to compute homotopy groups of spaces using a spectral sequence
Spectral sequence
In homological algebra and algebraic topology, a spectral sequence is a means of computing homology groups by taking successive approximations...
for special fibrations with Eilenberg–MacLane spaces for fibers.
The cohomology groups of Eilenberg–MacLane spaces can be used to classify all cohomology operation
Cohomology operation
In mathematics, the cohomology operation concept became central to algebraic topology, particularly homotopy theory, from the 1950s onwards, in the shape of the simple definition that if F is a functor defining a cohomology theory, then a cohomology operation should be a natural transformation from...
s.
See also
- Brown representability theorem, regarding representation spaces
- Moore space, the homology analogue.