Real projective space
Encyclopedia
In mathematics
, real projective space, or RPn, is the topological space
of lines through 0 in Rn+1. It is a compact
, smooth manifold of dimension n, and a special case of a Grassmannian
.
of Rn+1 − {0} under the equivalence relation
x ∼ λx for all real number
s λ ≠ 0. For all x in Rn+1 − {0} one can always find a λ such that λx has norm
1. There are precisely two such λ differing by sign.
Thus RPn can also be formed by identifying antipodal point
s of the unit n-sphere
, Sn, in Rn+1.
One can further restrict to the upper hemisphere of Sn and merely identify antipodal points on the bounding equator. This shows that RPn is also equivalent to the closed n-dimensional disk, Dn, with antipodal points on the boundary, ∂Dn = Sn−1, identified.
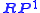is called the real projective line, which is topologically
equivalent to a circle
.
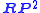is called the real projective plane
. This space cannot be embedded in R3. It can however be embedded in R4 and can be immersed in R3. The questions of embeddability and immersability for projective n-space have been well-studied.
is (diffeomorphic to) SO(3)
, hence admits a group structure; the covering map
is a map of groups 
, where Spin(3) is a Lie group
that is the universal cover of SO(3).
group action
on Sn. As mentioned above, the orbit space for this action is RPn. This action is actually a covering space action giving Sn as a double cover of RPn. Since Sn is simply connected for n ≥ 2, it also serves as the universal cover in these cases. It follows that the fundamental group
of RPn is Z2 when n > 1. (When n = 1 the fundamental group is Z due to the homeomorphism with S1). A generator for the fundamental group is the closed curve
obtained by projecting any curve connecting antipodal points in Sn down to RPn.
The projective n-space is compact connected and has a fundamental group isomorphic to the cyclic group of order 2: its universal covering space is given by the antipody quotient map from the n-sphere, a simply connected space. It is a double cover. The antipode map on
has
sign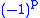
, so it is orientation-preserving iff p is even. The orientation character is thus: the non-trivial loop in 
acts as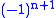 
on orientation, so
is orientable iff n+1 is even, i.e., n is odd.
The projective n-space is in fact diffeomorphic to the submanifold of R(n+1)2 consisting of all symmetric (n+1)x(n+1) matrices of trace 1 that are also idempotent linear transformations.
For the standard round metric, this has sectional curvature
identically 1.
In the standard round metric, the measure of projective space is exactly half the measure of the sphere.
.
with 1 cell in every dimension.
In homogeneous coordinates (x1 ... xn+1) on Sn, the coordinate neighborhood U1 = {(x1 ... xn+1)|x1 ≠ 0} can be identified with the interior of n-disk Dn. When xi = 0, one has RPn - 1. Therefore the n - 1 skeleton of RPn is RPn - 1, and the attaching map f: Sn-1 → RPn - 1 is the 2-to-1 covering map. One can put
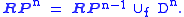
Induction shows that RPn is a CW complex with 1 cell in every dimension.
The cells are Schubert cells, as on the flag manifold
.
That is, take a complete flag (say the standard flag) 0 = V0 < V1 <...< Vn; then the closed k-cell is lines that lie in Vk. Also the open k-cell (the interior of the k-cell) is lines in Vk\Vk-1(lines in Vk but not Vk - 1).
In homogeneous coordinates (with respect to the flag), the cells are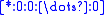
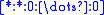
This is not a regular CW structure, as the attaching maps are 2-to-1. However, its cover is a regular CW structure on the sphere, with 2 cells in every dimension; indeed, the minimal regular CW structure on the sphere.
In light of the smooth structure, the existence of a Morse function would show RPn is a CW complex. One such function is given by, in homogeneous coordinates,
On each neighborhood Ui, g has nongenerate critical point (0...,1,...0) where 1 occurs in the i-th position with Morse index i. This shows RPn is a CW complex with 1 cell in every dimension.
over it, called the tautological bundle
. More precisely, this is called the tautological subbundle, and there is also a dual n-dimensional bundle called the tautological quotient bundle.
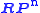are exactly the higher homotopy groups of 
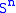, via the long exact sequence on homotopy associated to a fibration
.
Explicitly, the fiber bundle is:
You might also write this as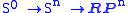
or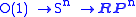
by analogy with complex projective space
.
The homotopy groups are: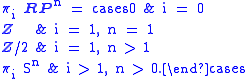
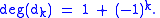
Thus the integral homology
is
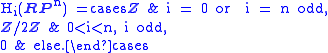
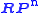is orientable iff n is odd, as the above homology calculation shows.
or union of the finite projective spaces:
Topologically, This space is double-covered by the infinite sphere
, which is contractible. The infinite projective space is therefore the Eilenberg-MacLane space
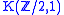and it is BO(1), the classifying space
for line bundle
s. More generally, the infinite Grassmannian
s are the classifying space
s for finite rank vector bundle
s.
Its cohomology ring
modulo
2 is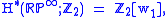
where
is the first Stiefel–Whitney class
:
it is the free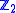
-algebra on 
, which has degree 1.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, real projective space, or RPn, is the topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
of lines through 0 in Rn+1. It is a compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
, smooth manifold of dimension n, and a special case of a Grassmannian
Grassmannian
In mathematics, a Grassmannian is a space which parameterizes all linear subspaces of a vector space V of a given dimension. For example, the Grassmannian Gr is the space of lines through the origin in V, so it is the same as the projective space P. The Grassmanians are compact, topological...
.
Construction
As with all projective spaces, RPn is formed by taking the quotientQuotient space
In topology and related areas of mathematics, a quotient space is, intuitively speaking, the result of identifying or "gluing together" certain points of a given space. The points to be identified are specified by an equivalence relation...
of Rn+1 − {0} under the equivalence relation
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
x ∼ λx for all real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s λ ≠ 0. For all x in Rn+1 − {0} one can always find a λ such that λx has norm
Norm (mathematics)
In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
1. There are precisely two such λ differing by sign.
Thus RPn can also be formed by identifying antipodal point
Antipodal point
In mathematics, the antipodal point of a point on the surface of a sphere is the point which is diametrically opposite to it — so situated that a line drawn from the one to the other passes through the centre of the sphere and forms a true diameter....
s of the unit n-sphere
Sphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
, Sn, in Rn+1.
One can further restrict to the upper hemisphere of Sn and merely identify antipodal points on the bounding equator. This shows that RPn is also equivalent to the closed n-dimensional disk, Dn, with antipodal points on the boundary, ∂Dn = Sn−1, identified.
Low-dimensional examples
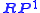is called the real projective line, which is topologicallyTopology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
equivalent to a circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
.
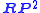is called the real projective planeReal projective plane
In mathematics, the real projective plane is an example of a compact non-orientable two-dimensional manifold, that is, a one-sided surface. It cannot be embedded in our usual three-dimensional space without intersecting itself...
. This space cannot be embedded in R3. It can however be embedded in R4 and can be immersed in R3. The questions of embeddability and immersability for projective n-space have been well-studied.
is (diffeomorphic to) SO(3)Rotation group
In mechanics and geometry, the rotation group is the group of all rotations about the origin of three-dimensional Euclidean space R3 under the operation of composition. By definition, a rotation about the origin is a linear transformation that preserves length of vectors and preserves orientation ...
, hence admits a group structure; the covering map
is a map of groups , where Spin(3) is a Lie groupLie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
that is the universal cover of SO(3).
Topology
The antipodal map on the n-sphere (the map sending x to −x) generates a Z2Cyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
group action
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
on Sn. As mentioned above, the orbit space for this action is RPn. This action is actually a covering space action giving Sn as a double cover of RPn. Since Sn is simply connected for n ≥ 2, it also serves as the universal cover in these cases. It follows that the fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
of RPn is Z2 when n > 1. (When n = 1 the fundamental group is Z due to the homeomorphism with S1). A generator for the fundamental group is the closed curve
Curve
In mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...
obtained by projecting any curve connecting antipodal points in Sn down to RPn.
The projective n-space is compact connected and has a fundamental group isomorphic to the cyclic group of order 2: its universal covering space is given by the antipody quotient map from the n-sphere, a simply connected space. It is a double cover. The antipode map on
hassign
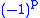, so it is orientation-preserving iff p is even. The orientation character is thus: the non-trivial loop in acts as 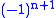on orientation, so is orientable iff n+1 is even, i.e., n is odd.The projective n-space is in fact diffeomorphic to the submanifold of R(n+1)2 consisting of all symmetric (n+1)x(n+1) matrices of trace 1 that are also idempotent linear transformations.
Geometry of real projective spaces
Real projective space admits a constant positive scalar curvature metric, coming from the double cover by the standard round sphere (the antipodal map is an isometry).For the standard round metric, this has sectional curvature
Sectional curvature
In Riemannian geometry, the sectional curvature is one of the ways to describe the curvature of Riemannian manifolds. The sectional curvature K depends on a two-dimensional plane σp in the tangent space at p...
identically 1.
In the standard round metric, the measure of projective space is exactly half the measure of the sphere.
Smooth structure
Real projective spaces are smooth manifolds. On Sn, in homogeneous coordinates, (x1...xn+1), consider the subset Ui with xi ≠ 0. Each Ui is homeomorphic to the open unit ball in Rn and the coordinate transition functions are smooth. This gives RPn a smooth structureSmooth structure
In mathematics, a smooth structure on a manifold allows for an unambiguous notion of smooth function. In particular, a smooth structure allows one to perform mathematical analysis on the manifold....
.
CW structure
Real projective space RPn admits a CW structureCW complex
In topology, a CW complex is a type of topological space introduced by J. H. C. Whitehead to meet the needs of homotopy theory. This class of spaces is broader and has some better categorical properties than simplicial complexes, but still retains a combinatorial naturethat allows for...
with 1 cell in every dimension.
In homogeneous coordinates (x1 ... xn+1) on Sn, the coordinate neighborhood U1 = {(x1 ... xn+1)|x1 ≠ 0} can be identified with the interior of n-disk Dn. When xi = 0, one has RPn - 1. Therefore the n - 1 skeleton of RPn is RPn - 1, and the attaching map f: Sn-1 → RPn - 1 is the 2-to-1 covering map. One can put
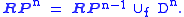
Induction shows that RPn is a CW complex with 1 cell in every dimension.
The cells are Schubert cells, as on the flag manifold
Flag manifold
In mathematics, a generalized flag variety is a homogeneous space whose points are flags in a finite-dimensional vector space V over a field F. When F is the real or complex numbers, a generalized flag variety is a smooth or complex manifold, called a real or complex flag manifold...
.
That is, take a complete flag (say the standard flag) 0 = V0 < V1 <...< Vn; then the closed k-cell is lines that lie in Vk. Also the open k-cell (the interior of the k-cell) is lines in Vk\Vk-1(lines in Vk but not Vk - 1).
In homogeneous coordinates (with respect to the flag), the cells are
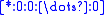
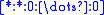
This is not a regular CW structure, as the attaching maps are 2-to-1. However, its cover is a regular CW structure on the sphere, with 2 cells in every dimension; indeed, the minimal regular CW structure on the sphere.
In light of the smooth structure, the existence of a Morse function would show RPn is a CW complex. One such function is given by, in homogeneous coordinates,
On each neighborhood Ui, g has nongenerate critical point (0...,1,...0) where 1 occurs in the i-th position with Morse index i. This shows RPn is a CW complex with 1 cell in every dimension.
Tautological bundles
Real projective space has a natural line bundleLine bundle
In mathematics, a line bundle expresses the concept of a line that varies from point to point of a space. For example a curve in the plane having a tangent line at each point determines a varying line: the tangent bundle is a way of organising these...
over it, called the tautological bundle
Tautological bundle
In mathematics, tautological bundle is a term for a particularly natural vector bundle occurring over a Grassmannian, and more specially over projective space...
. More precisely, this is called the tautological subbundle, and there is also a dual n-dimensional bundle called the tautological quotient bundle.
Homotopy groups
The higher homotopy groups of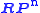 are exactly the higher homotopy groups of 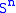, via the long exact sequence on homotopy associated to a fibrationFibration
In topology, a branch of mathematics, a fibration is a generalization of the notion of a fiber bundle. A fiber bundle makes precise the idea of one topological space being "parameterized" by another topological space . A fibration is like a fiber bundle, except that the fibers need not be the same...
.
Explicitly, the fiber bundle is:
You might also write this as
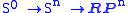
or
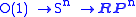
by analogy with complex projective space
Complex projective space
In mathematics, complex projective space is the projective space with respect to the field of complex numbers. By analogy, whereas the points of a real projective space label the lines through the origin of a real Euclidean space, the points of a complex projective space label the complex lines...
.
The homotopy groups are:
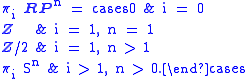
Homology
The cellular chain complex associated to the above CW structure has 1 cell in each dimension 0,...,n. For each dimensional k, the boundary maps dk : δDk → RPk-1/RPk-2 is the map that collapses the equator on Sk - 1 and then identifies antipodal points. In odd (resp. even) dimensions, this has degree 0 (resp. 2):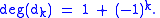Thus the integral homology
Cellular homology
In mathematics, cellular homology in algebraic topology is a homology theory for CW-complexes. It agrees with singular homology, and can provide an effective means of computing homology modules.- Definition :...
is
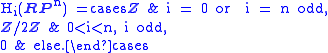
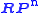is orientable iff n is odd, as the above homology calculation shows.Infinite real projective space
The infinite real projective space is constructed as the direct limitDirect limit
In mathematics, a direct limit is a colimit of a "directed family of objects". We will first give the definition for algebraic structures like groups and modules, and then the general definition which can be used in any category.- Algebraic objects :In this section objects are understood to be...
or union of the finite projective spaces:
Topologically, This space is double-covered by the infinite sphere
, which is contractible. The infinite projective space is therefore the Eilenberg-MacLane spaceEilenberg-MacLane space
In mathematics, an Eilenberg–MacLane spaceSaunders Mac Lane originally spelt his name "MacLane" , and co-published the papers establishing the notion of Eilenberg–MacLane spaces under this name. In mathematics, an Eilenberg–MacLane spaceSaunders Mac Lane originally spelt his name "MacLane" (without...
and it is BO(1), the classifying spaceClassifying space
In mathematics, specifically in homotopy theory, a classifying space BG of a topological group G is the quotient of a weakly contractible space EG by a free action of G...
for line bundle
Line bundle
In mathematics, a line bundle expresses the concept of a line that varies from point to point of a space. For example a curve in the plane having a tangent line at each point determines a varying line: the tangent bundle is a way of organising these...
s. More generally, the infinite Grassmannian
Grassmannian
In mathematics, a Grassmannian is a space which parameterizes all linear subspaces of a vector space V of a given dimension. For example, the Grassmannian Gr is the space of lines through the origin in V, so it is the same as the projective space P. The Grassmanians are compact, topological...
s are the classifying space
Classifying space
In mathematics, specifically in homotopy theory, a classifying space BG of a topological group G is the quotient of a weakly contractible space EG by a free action of G...
s for finite rank vector bundle
Vector bundle
In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
s.
Its cohomology ring
Cohomology ring
In mathematics, specifically algebraic topology, the cohomology ring of a topological space X is a ring formed from the cohomology groups of X together with the cup product serving as the ring multiplication. Here 'cohomology' is usually understood as singular cohomology, but the ring structure is...
modulo
Modulo
In the mathematical community, the word modulo is often used informally. Generally, to say "A is the same as B modulo C" means, more-or-less, "A and B are the same except for differences accounted for or explained by C"....
2 is
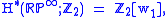
where
is the first Stiefel–Whitney classStiefel–Whitney class
In mathematics, in particular in algebraic topology and differential geometry, the Stiefel–Whitney class is an example of a \mathbb Z_2characteristic class associated to real vector bundles.-General presentation:...
:
it is the free
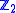-algebra on , which has degree 1.