
Orientation character
Encyclopedia
In algebraic topology
, a branch of mathematics
, an orientation character on a group
 is a group homomorphism
is a group homomorphism
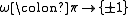 . This notion is of particular significance in surgery theory
. This notion is of particular significance in surgery theory
.
M, one takes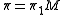 (the fundamental group
(the fundamental group
), and then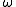 sends an element of
sends an element of  to
to  if and only if the class it represents is orientation-reversing.
if and only if the class it represents is orientation-reversing.
This map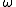 is trivial if and only if M is orientable.
is trivial if and only if M is orientable.
The orientation character is an algebraic structure on the fundamental group of a manifold, which captures which loops are orientation reversing and which are orientation preserving.
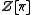 , by
, by 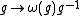 (i.e.,
(i.e.,  , accordingly as
, accordingly as 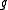 is orientation preserving or reversing). This is denoted
is orientation preserving or reversing). This is denoted 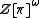 .
.
Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
, a branch of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, an orientation character on a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
 is a group homomorphism
is a group homomorphismGroup homomorphism
In mathematics, given two groups and , a group homomorphism from to is a function h : G → H such that for all u and v in G it holds that h = h \cdot h...
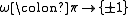 . This notion is of particular significance in surgery theory
. This notion is of particular significance in surgery theorySurgery theory
In mathematics, specifically in geometric topology, surgery theory is a collection of techniques used to produce one manifold from another in a 'controlled' way, introduced by . Surgery refers to cutting out parts of the manifold and replacing it with a part of another manifold, matching up along...
.
Motivation
Given a manifoldManifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
M, one takes
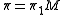 (the fundamental group
(the fundamental groupFundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
), and then
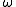 sends an element of
sends an element of  to
to  if and only if the class it represents is orientation-reversing.
if and only if the class it represents is orientation-reversing.This map
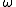 is trivial if and only if M is orientable.
is trivial if and only if M is orientable.The orientation character is an algebraic structure on the fundamental group of a manifold, which captures which loops are orientation reversing and which are orientation preserving.
Twisted group algebra
The orientation character defines a twisted involution (*-ring structure) on the group ringGroup ring
In algebra, a group ring is a free module and at the same time a ring, constructed in a natural way from any given ring and any given group. As a free module, its ring of scalars is the given ring and its basis is one-to-one with the given group. As a ring, its addition law is that of the free...
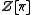 , by
, by 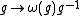 (i.e.,
(i.e.,  , accordingly as
, accordingly as 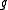 is orientation preserving or reversing). This is denoted
is orientation preserving or reversing). This is denoted 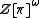 .
.Examples
- In real projective spaceReal projective spaceIn mathematics, real projective space, or RPn, is the topological space of lines through 0 in Rn+1. It is a compact, smooth manifold of dimension n, and a special case of a Grassmannian.-Construction:...
s, the orientation character evaluates trivially on loops if the dimension is odd, and assigns -1 to noncontractible loops in even dimension.

