Surgery theory
Encyclopedia
In mathematics
, specifically in geometric topology
, surgery theory is a collection of techniques used to produce one manifold
from another in a 'controlled' way, introduced by . Surgery refers to cutting out parts of the manifold and replacing it with a part of another manifold, matching up along the cut or boundary. This is closely related to, but not identical with, handlebody
decompositions. It is a major tool in the study and classification of manifolds of dimension greater than 4.
More technically, the idea is to start with a well-understood manifold
and perform surgery on it to produce a manifold 
having some desired property, in such a way that the effects on the homology
, homotopy group
s, or other interesting invariants of the manifold are known.
The classification of exotic sphere
s by led to the emergence of surgery theory as a major tool in high-dimensional topology.
, 
are manifolds with boundary, then the boundary of the product manifold is 
. The basic observation which justifies surgery is that the space 
can be understood either as the boundary of 
or as the boundary of 
. In symbols, 
.
Now, given a manifold
of dimension 
and an embedding
, define another 
-dimensional manifold 
to be
One says that the manifold
is produced by a surgery cutting out 
and gluing in 
,
or by a
-surgery if one wants to specify the number 
. Strictly speaking, 
is a manifold with corners, but there is a canonical way to smooth them out. Notice that the submanifold that was replaced in 
was of the same dimension as 
(it was of codimension
0).
Surgery is closely related to (but not the same as) handle attaching
. Given an
-manifold with boundary 
and an embedding 
, where 
, define another 
-manifold with boundary 
by
The manifold
is obtained by attaching a 
-handle, with 
obtained from 
by a 
-surgery
A surgery on
not only produces a new manifold 
, but also a cobordism 
between 
and 
. The trace of the surgery is the cobordism 
, with
the
-dimensional manifold with boundary 
obtained from
the product
by attaching a 
-handle 
.
Surgery is symmetric in the sense that the manifold
can be re-obtained from 
by a 
-surgery, the trace of which coincides with the trace of the original surgery, up to orientation.
In most applications, the manifold
comes with additional geometric structure, such as a map to some reference space, or additional bundle data. One then wants the surgery process to endow 
with the same kind of additional structure. For instance, a standard tool in surgery theory is surgery on normal maps
: such a process changes a normal map to another normal map within the same bordism class.
As per the above definition, a surgery on the circle consists of cutting out a copy of 
and gluing in 
. The pictures in Fig. 1 show that the result of doing this is either (i) 
again, or (ii) two copies of 
.
2. Surgery on the 2-sphere
In this case there are more possibilities, since we can start by cutting out either
or 
.
3. Surgery on the n-sphere
If
, then 
. The p-surgery on 
is therefore 
. Examples 1 and 2 above were a special case of this.
4. Morse functions
Suppose that
is a Morse function on an 
-dimensional manifold, and suppose that 
is a critical value with exactly one critical point in its preimage. If the index of this critical point is 
, then the level-set 
is obtained from 
by a 
-surgery. The bordism 
can be identified with the trace of this surgery.
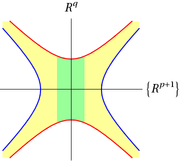Indeed, in some coordinate chart around the critical point, the function 
is of the form 
, with 
, and 
. Fig. 3 shows, in this local chart, the manifold 
in blue and the manifold 
in red. The colored region between 
and 
corresponds to the bordism 
. The picture shows that 
is diffeomorphic to the union
(neglecting the issue of straightening corners), where
is colored in yellow, and 
is colored in green. The manifold 
, being a boundary component of 
, is therefore obtained from 
by a 
-surgery.
Since every bordism between closed manifolds has a Morse function where different critical points have different critical values, this shows that any bordism can be decomposed into traces of surgeries (handlebody decomposition). In particular, every manifold
may be regarded as a bordism from the boundary 
(which may be empty) to the empty manifold, and so may be obtained from
by attaching handles.
takes the place of the attaching map. A simple attachment of a 
-cell to an 
-manifold would destroy the manifold structure for dimension reasons, so it has to be thickened by crossing with another cell.
Up to homotopy, the process of surgery on an embedding
can be described as the attaching of a 
-cell, giving the homotopy type of the trace, and the detaching of a 
-cell to obtain 
. The necessity of the detaching process can be understood as an effect of Poincaré duality
.
In the same way as a cell can be attached to a space to kill an element in some homotopy group
of the space, a
-surgery on a manifold 
can often be used to kill an element 
. Two points are important however: Firstly, the element 
has to be representable by an embedding 
(which means embedding the corresponding sphere with a trivial normal bundle
). For instance, it is not possible to perform surgery on an orientation-reversing loop. Secondly, the effect of the detaching process has to be considered, since it might also have an effect on the homotopy group under consideration. Roughly speaking, this second point is only important when
is at least of the order of half the dimension of 
.
of dimension greater than four. Loosely, the organizing questions of surgery theory are:
More formally, one must ask whether up to homotopy
:
It turns out that the second ("uniqueness") question is a relative version of a question of the first ("existence") type; thus both questions can be treated with the same methods.
Note that surgery theory does not give a complete set of invariants
to these questions. Instead, it is obstruction-theoretic
: there is a primary obstruction, and a secondary obstruction called the surgery obstruction which is only defined if the
primary obstruction vanishes, and which depends on the choice made in verifying that the primary obstruction vanishes.
, Novikov, Sullivan
and Wall
, surgery is done on normal maps
of degree one. Using surgery, the question "Is the normal map
of degree one cobordant to a homotopy equivalence?" can be translated (in dimensions greater than four) to an algebraic statement about some element in an L-group
of the group ring
. More precisely, the question has a positive answer if and only if the surgery obstruction 
is zero, where n is the dimension of M.
For example, consider the case where the dimension n=4k is a multiple of four, and
. It is known that 
is isomorphic to 
; under this isomorphism the surgery obstruction of f maps, up to a scalar factor, to the difference of the signature
s
of X and M. Hence a normal map of degree one is cobordant to a homotopy equivalence if and only if the signatures of domain and codomain agree.
Coming back to the "existence" question from above, we see that a space X has the homotopy type of a smooth manifold if and only if it receives a normal map of degree one whose surgery obstruction vanishes. This leads to a multi-step obstruction process: In order to speak of normal maps, X must satisfy an appropriate version of Poincaré duality
which turns it into a Poincaré complex
. Supposing that X is a Poincaré complex, the Pontryagin-Thom construction shows that a normal map of degree one to X exists if and only if the Spivak normal fibration of X has a reduction to a stable vector bundle. If normal maps of degree one to X exist, their bordism classes (called normal invariants) are classified by the set of homotopy classes
. Each of these normal invariants has a surgery obstruction; X has the homotopy type of a smooth manifold if and only if one of these obstructions is zero. Stated differently, this means that there is a choice of normal invariant with zero image under the surgery obstruction map
consists of homotopy equivalences 
from some manifold to X, where two maps are identified under a bordism-type relation. A necessary (but not in general sufficient) condition for the structure set of a space 
to be non-empty is that 
be an 
-dimensional Poincaré complex, i.e. that the homology
and cohomology
groups be related by isomorphisms
of an 
-dimensional manifold, for some integer 
. Depending on the precise definition and the category of manifolds (smooth
, PL
, or topological
), there are various versions of structure sets. Since, by the s-cobordism theorem, certain bordisms between manifolds are isomorphic (in the respective category) to cylinders, the concept of structure set allows a classification even up to diffeomorphism
.
The structure set and the surgery obstruction map are brought together in the surgery exact sequence. This sequence allows to determine the structure set of a Poincaré complex once the surgery obstruction map (and a relative version of it) are understood. In important cases, the smooth or topological structure set can be computed by means of the surgery exact sequence. Examples are the classification of exotic sphere
s, and the proofs of the Borel conjecture
for negatively curved
manifolds and manifolds with hyperbolic
fundamental group.
In the topological category, the surgery exact sequence is the long exact sequence induced by a fibration sequence of spectra
. This implies that all the sets involved in the sequence are in fact abelian groups. On the spectrum level, the surgery obstruction map is an assembly map
whose fiber is the block structure space of the corresponding manifold.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, specifically in geometric topology
Geometric topology
In mathematics, geometric topology is the study of manifolds and maps between them, particularly embeddings of one manifold into another.- Topics :...
, surgery theory is a collection of techniques used to produce one manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
from another in a 'controlled' way, introduced by . Surgery refers to cutting out parts of the manifold and replacing it with a part of another manifold, matching up along the cut or boundary. This is closely related to, but not identical with, handlebody
Handlebody
In the mathematical field of geometric topology, a handlebody is a decomposition of a manifold into standard pieces. Handlebodies play an important role in Morse theory, cobordism theory and the surgery theory of high-dimensional manifolds...
decompositions. It is a major tool in the study and classification of manifolds of dimension greater than 4.
More technically, the idea is to start with a well-understood manifold
and perform surgery on it to produce a manifold having some desired property, in such a way that the effects on the homologyHomology (mathematics)
In mathematics , homology is a certain general procedure to associate a sequence of abelian groups or modules with a given mathematical object such as a topological space or a group...
, homotopy group
Homotopy group
In mathematics, homotopy groups are used in algebraic topology to classify topological spaces. The first and simplest homotopy group is the fundamental group, which records information about loops in a space...
s, or other interesting invariants of the manifold are known.
The classification of exotic sphere
Exotic sphere
In differential topology, a mathematical discipline, an exotic sphere is a differentiable manifold M that is homeomorphic but not diffeomorphic to the standard Euclidean n-sphere...
s by led to the emergence of surgery theory as a major tool in high-dimensional topology.
Surgery on a manifold
Recall that in general, if, are manifolds with boundary, then the boundary of the product manifold is . The basic observation which justifies surgery is that the space can be understood either as the boundary of or as the boundary of . In symbols, .Now, given a manifold
of dimension and an embeddingEmbedding
In mathematics, an embedding is one instance of some mathematical structure contained within another instance, such as a group that is a subgroup....
, define another -dimensional manifold to beOne says that the manifold
is produced by a surgery cutting out and gluing in ,or by a
-surgery if one wants to specify the number . Strictly speaking, is a manifold with corners, but there is a canonical way to smooth them out. Notice that the submanifold that was replaced in was of the same dimension as (it was of codimensionCodimension
In mathematics, codimension is a basic geometric idea that applies to subspaces in vector spaces, and also to submanifolds in manifolds, and suitable subsets of algebraic varieties.The dual concept is relative dimension.-Definition:...
0).
Surgery is closely related to (but not the same as) handle attaching
Handlebody
In the mathematical field of geometric topology, a handlebody is a decomposition of a manifold into standard pieces. Handlebodies play an important role in Morse theory, cobordism theory and the surgery theory of high-dimensional manifolds...
. Given an
-manifold with boundary and an embedding , where , define another -manifold with boundary byThe manifold
is obtained by attaching a -handle, with obtained from by a -surgeryA surgery on
not only produces a new manifold , but also a cobordism between and . The trace of the surgery is the cobordism , withthe
-dimensional manifold with boundary obtained fromthe product
by attaching a -handle .Surgery is symmetric in the sense that the manifold
can be re-obtained from by a -surgery, the trace of which coincides with the trace of the original surgery, up to orientation.In most applications, the manifold
comes with additional geometric structure, such as a map to some reference space, or additional bundle data. One then wants the surgery process to endow with the same kind of additional structure. For instance, a standard tool in surgery theory is surgery on normal mapsNormal invariants
In mathematics, a normal map is a concept in geometric topology due to William Browder which is of fundamental importance in surgery theory. Given a Poincaré complex X, a normal map on X endows the space, roughly speaking, with some of the homotopy-theoretic global structure of a closed manifold...
: such a process changes a normal map to another normal map within the same bordism class.
Examples
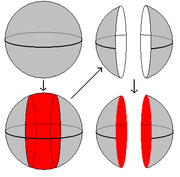
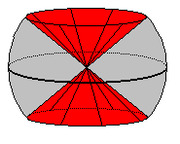
1. Surgery on the circle and gluing in . The pictures in Fig. 1 show that the result of doing this is either (i) again, or (ii) two copies of .In this case there are more possibilities, since we can start by cutting out either
or .- (a)
: If we remove a cylinder from the 2-sphere, we are left with two disks. We have to glue back in 
- that is, two disks - and it's clear that the result of doing so is to give us two disjoint spheres. (Fig. 2a)
- (b)
: Having cut out two disks 
, we glue back in the cylinder 
. Interestingly, there are two possible outcomes, depending on whether our glueing maps have the same or opposite orientation on the two boundary circles. If the orientations are the same (Fig. 2b), the resulting manifold is the torusTorusIn geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
, but if they are different, we obtain the Klein BottleKlein bottleIn mathematics, the Klein bottle is a non-orientable surface, informally, a surface in which notions of left and right cannot be consistently defined. Other related non-orientable objects include the Möbius strip and the real projective plane. Whereas a Möbius strip is a surface with boundary, a...
(Fig. 2c).
3. Surgery on the n-sphere
If
, then . The p-surgery on is therefore . Examples 1 and 2 above were a special case of this.4. Morse functions
Suppose that
is a Morse function on an -dimensional manifold, and suppose that is a critical value with exactly one critical point in its preimage. If the index of this critical point is , then the level-set is obtained from by a -surgery. The bordism can be identified with the trace of this surgery. is of the form , with , and . Fig. 3 shows, in this local chart, the manifold 
in blue and the manifold in red. The colored region between and corresponds to the bordism . The picture shows that is diffeomorphic to the union(neglecting the issue of straightening corners), where
is colored in yellow, and is colored in green. The manifold , being a boundary component of , is therefore obtained from by a -surgery.Since every bordism between closed manifolds has a Morse function where different critical points have different critical values, this shows that any bordism can be decomposed into traces of surgeries (handlebody decomposition). In particular, every manifold
may be regarded as a bordism from the boundary (which may be empty) to the empty manifold, and so may be obtained from
by attaching handles.Effects on homotopy groups, and comparison to cell-attachment
Intuitively, the process of surgery is the manifold analog of attaching a cell to a topological space, where the embedding takes the place of the attaching map. A simple attachment of a -cell to an -manifold would destroy the manifold structure for dimension reasons, so it has to be thickened by crossing with another cell.Up to homotopy, the process of surgery on an embedding
can be described as the attaching of a -cell, giving the homotopy type of the trace, and the detaching of a -cell to obtain . The necessity of the detaching process can be understood as an effect of Poincaré dualityPoincaré duality
In mathematics, the Poincaré duality theorem named after Henri Poincaré, is a basic result on the structure of the homology and cohomology groups of manifolds...
.
In the same way as a cell can be attached to a space to kill an element in some homotopy group
Homotopy group
In mathematics, homotopy groups are used in algebraic topology to classify topological spaces. The first and simplest homotopy group is the fundamental group, which records information about loops in a space...
of the space, a
-surgery on a manifold can often be used to kill an element . Two points are important however: Firstly, the element has to be representable by an embedding (which means embedding the corresponding sphere with a trivial normal bundleNormal bundle
In differential geometry, a field of mathematics, a normal bundle is a particular kind of vector bundle, complementary to the tangent bundle, and coming from an embedding .-Riemannian manifold:...
). For instance, it is not possible to perform surgery on an orientation-reversing loop. Secondly, the effect of the detaching process has to be considered, since it might also have an effect on the homotopy group under consideration. Roughly speaking, this second point is only important when
is at least of the order of half the dimension of .Application to classification of manifolds
The origin and main application of surgery theory lies in the classification of manifoldsClassification of manifolds
In mathematics, specifically geometry and topology, the classification of manifolds is a basic question, about which much is known, and many open questions remain.-Overview:...
of dimension greater than four. Loosely, the organizing questions of surgery theory are:
- Is X a manifold?
- Is f a diffeomorphism?
More formally, one must ask whether up to homotopy
Homotopy
In topology, two continuous functions from one topological space to another are called homotopic if one can be "continuously deformed" into the other, such a deformation being called a homotopy between the two functions...
:
- Does a space X have the homotopy type of a smooth manifold?
- Is a homotopy equivalence
between two smooth manifolds homotopic to a diffeomorphism?
It turns out that the second ("uniqueness") question is a relative version of a question of the first ("existence") type; thus both questions can be treated with the same methods.
Note that surgery theory does not give a complete set of invariants
Complete set of invariants
In mathematics, a complete set of invariants for a classification problem is a collection of mapsf_i : X \to Y_i \,, such that x ∼ x' if and only if f_i = f_i for all i...
to these questions. Instead, it is obstruction-theoretic
Obstruction theory
In mathematics, obstruction theory is a name given to two different mathematical theories, both of which yield cohomological invariants.-In homotopy theory:...
: there is a primary obstruction, and a secondary obstruction called the surgery obstruction which is only defined if the
primary obstruction vanishes, and which depends on the choice made in verifying that the primary obstruction vanishes.
The surgery approach
In the classical approach, as developed by BrowderWilliam Browder (mathematician)
William Browder is an American mathematician, specializing in algebraic topology, differential topology and differential geometry...
, Novikov, Sullivan
Dennis Sullivan
Dennis Parnell Sullivan is an American mathematician. He is known for work in topology, both algebraic and geometric, and on dynamical systems. He holds the Albert Einstein Chair at the City University of New York Graduate Center, and is a professor at Stony Brook University.-Work in topology:He...
and Wall
C. T. C. Wall
Charles Terence Clegg Wall is a leading British mathematician, educated at Marlborough and Trinity College, Cambridge. He is an emeritus professor of the University of Liverpool, where he was first appointed Professor in 1965...
, surgery is done on normal maps
Normal invariants
In mathematics, a normal map is a concept in geometric topology due to William Browder which is of fundamental importance in surgery theory. Given a Poincaré complex X, a normal map on X endows the space, roughly speaking, with some of the homotopy-theoretic global structure of a closed manifold...
of degree one. Using surgery, the question "Is the normal map
of degree one cobordant to a homotopy equivalence?" can be translated (in dimensions greater than four) to an algebraic statement about some element in an L-groupL-theory
Algebraic L-theory is the K-theory of quadratic forms; the term was coined by C. T. C. Wall,with L being used as the letter after K. Algebraic L-theory, also known as 'hermitian K-theory',is important in surgery theory.-Definition:...
of the group ring
Group ring
In algebra, a group ring is a free module and at the same time a ring, constructed in a natural way from any given ring and any given group. As a free module, its ring of scalars is the given ring and its basis is one-to-one with the given group. As a ring, its addition law is that of the free...
. More precisely, the question has a positive answer if and only if the surgery obstruction is zero, where n is the dimension of M.For example, consider the case where the dimension n=4k is a multiple of four, and
. It is known that is isomorphic to ; under this isomorphism the surgery obstruction of f maps, up to a scalar factor, to the difference of the signatureSignature
A signature is a handwritten depiction of someone's name, nickname, or even a simple "X" that a person writes on documents as a proof of identity and intent. The writer of a signature is a signatory. Similar to a handwritten signature, a signature work describes the work as readily identifying...
s
of X and M. Hence a normal map of degree one is cobordant to a homotopy equivalence if and only if the signatures of domain and codomain agree.Coming back to the "existence" question from above, we see that a space X has the homotopy type of a smooth manifold if and only if it receives a normal map of degree one whose surgery obstruction vanishes. This leads to a multi-step obstruction process: In order to speak of normal maps, X must satisfy an appropriate version of Poincaré duality
Poincaré duality
In mathematics, the Poincaré duality theorem named after Henri Poincaré, is a basic result on the structure of the homology and cohomology groups of manifolds...
which turns it into a Poincaré complex
Poincaré complex
In mathematics, and especially topology, a Poincaré complex is a generalisation of a manifold.The homology groups of a closed, orientable manifold are related in certain ways. This relationship came to be known as the Poincaré duality. Poincaré duality gives an isomorphism between homology and...
. Supposing that X is a Poincaré complex, the Pontryagin-Thom construction shows that a normal map of degree one to X exists if and only if the Spivak normal fibration of X has a reduction to a stable vector bundle. If normal maps of degree one to X exist, their bordism classes (called normal invariants) are classified by the set of homotopy classes
. Each of these normal invariants has a surgery obstruction; X has the homotopy type of a smooth manifold if and only if one of these obstructions is zero. Stated differently, this means that there is a choice of normal invariant with zero image under the surgery obstruction mapStructure sets and surgery exact sequence
The concept of structure set is the unifying framework for both questions of existence and uniqueness. Roughly speaking, the structure set of a space consists of homotopy equivalences from some manifold to X, where two maps are identified under a bordism-type relation. A necessary (but not in general sufficient) condition for the structure set of a space to be non-empty is that be an -dimensional Poincaré complex, i.e. that the homologyHomology (mathematics)
In mathematics , homology is a certain general procedure to associate a sequence of abelian groups or modules with a given mathematical object such as a topological space or a group...
and cohomology
Cohomology
In mathematics, specifically in algebraic topology, cohomology is a general term for a sequence of abelian groups defined from a co-chain complex. That is, cohomology is defined as the abstract study of cochains, cocycles, and coboundaries...
groups be related by isomorphisms
of an -dimensional manifold, for some integer . Depending on the precise definition and the category of manifolds (smoothDifferentiable manifold
A differentiable manifold is a type of manifold that is locally similar enough to a linear space to allow one to do calculus. Any manifold can be described by a collection of charts, also known as an atlas. One may then apply ideas from calculus while working within the individual charts, since...
, PL
Piecewise linear manifold
In mathematics, a piecewise linear manifold is a topological manifold together with a piecewise linear structure on it. Such a structure can be defined by means of an atlas, such that one can pass from chart to chart in it by piecewise linear functions.An isomorphism of PL manifolds is called a PL...
, or topological
Topological manifold
In mathematics, a topological manifold is a topological space which looks locally like Euclidean space in a sense defined below...
), there are various versions of structure sets. Since, by the s-cobordism theorem, certain bordisms between manifolds are isomorphic (in the respective category) to cylinders, the concept of structure set allows a classification even up to diffeomorphism
Diffeomorphism
In mathematics, a diffeomorphism is an isomorphism in the category of smooth manifolds. It is an invertible function that maps one differentiable manifold to another, such that both the function and its inverse are smooth.- Definition :...
.
The structure set and the surgery obstruction map are brought together in the surgery exact sequence. This sequence allows to determine the structure set of a Poincaré complex once the surgery obstruction map (and a relative version of it) are understood. In important cases, the smooth or topological structure set can be computed by means of the surgery exact sequence. Examples are the classification of exotic sphere
Exotic sphere
In differential topology, a mathematical discipline, an exotic sphere is a differentiable manifold M that is homeomorphic but not diffeomorphic to the standard Euclidean n-sphere...
s, and the proofs of the Borel conjecture
Borel conjecture
In mathematics, specifically geometric topology, the Borel conjecture asserts that an aspherical closed manifold is determined by its fundamental group, up to homeomorphism...
for negatively curved
Scalar curvature
In Riemannian geometry, the scalar curvature is the simplest curvature invariant of a Riemannian manifold. To each point on a Riemannian manifold, it assigns a single real number determined by the intrinsic geometry of the manifold near that point...
manifolds and manifolds with hyperbolic
Hyperbolic group
In group theory, a hyperbolic group, also known as a word hyperbolic group, Gromov hyperbolic group, negatively curved group is a finitely generated group equipped with a word metric satisfying certain properties characteristic of hyperbolic geometry. The notion of a hyperbolic group was introduced...
fundamental group.
In the topological category, the surgery exact sequence is the long exact sequence induced by a fibration sequence of spectra
Spectrum (homotopy theory)
In algebraic topology, a branch of mathematics, a spectrum is an object representing a generalized cohomology theory. There are several different constructions of categories of spectra, any of which gives a context for the same stable homotopy theory....
. This implies that all the sets involved in the sequence are in fact abelian groups. On the spectrum level, the surgery obstruction map is an assembly map
Assembly map
In mathematics, assembly maps are an important concept in geometric topology. From the homotopy-theoretical viewpoint, an assembly map is a universal approximation of a homotopy invariant functor by a homology theory from the left...
whose fiber is the block structure space of the corresponding manifold.
See also
- s-cobordism theorem
- h-cobordism theorem
- Whitehead torsionWhitehead torsionIn geometric topology, the obstruction to a homotopy equivalence f\colon X \to Y of finite CW-complexes being a simple homotopy equivalence is its Whitehead torsion \tau, which is an element in the Whitehead group Wh. These are named after the mathematician J. H. C...
- Dehn surgeryDehn surgeryIn topology, a branch of mathematics, a Dehn surgery, named after Max Dehn, is a specific construction used to modify 3-manifolds. The process takes as input a 3-manifold together with a link...
- Manifold decompositionManifold decompositionIn topology, a branch of mathematics, a manifold M may be decomposed or split by writing M as a combination of smaller pieces. When doing so, one must specify both what those pieces are and how they are put together to form M....
- orientation character