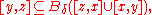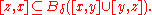Hyperbolic group
Encyclopedia
In group theory
, a hyperbolic group, also known as a word hyperbolic group, Gromov hyperbolic group, negatively curved group is a finitely generated group
equipped with a word metric satisfying certain properties characteristic of hyperbolic geometry
. The notion of a hyperbolic group was introduced and developed by Mikhail Gromov in the early 1980s. He noticed that many results of Max Dehn
concerning the fundamental group
of a hyperbolic Riemann surface
do not rely either on it having dimension two or even on being a manifold
and hold in much more general context. In a very influential paper from 1987, Gromov proposed a wide-ranging research program. Ideas and foundational material in the theory of hyperbolic groups also stem from the work of George Mostow
, William Thurston
, James W. Cannon
, Eliyahu Rips
, and many others.
of the group and involve a choice of a positive constant δ and first define a δ-hyperbolic group. A group is called hyperbolic if it is δ-hyperbolic for some δ. When translating between different definitions of hyperbolicity, the particular value of δ may change, but the resulting notions of a hyperbolic group turn out to be equivalent.
Let G be a finitely generated group, and T be its Cayley graph
with respect to some finite set S of generators. By identifying each edge isometrically with the unit interval in R, the Cayley graph becomes a metric space
. The group G acts on T by isometries
and this action is simply transitive on the vertices. A path in T of minimal length that connects points x and y is called a geodesic segment and is denoted [x,y]. A geodesic triangle in T consists of three points x, y, z, its vertices, and three geodesic segments [x,y], [y,z], [z,x], its sides.
The first approach to hyperbolicity is based on the slim triangles condition and is generally credited to Rips. Let δ > 0 be fixed. A geodesic triangle is δ-slim if each side is contained in a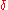 -neighborhood of the other two sides:
-neighborhood of the other two sides:
The Cayley graph T is δ-hyperbolic if all geodesic triangles are δ-slim, and in this case G is a δ-hyperbolic group. Although a different choice of a finite generating set will lead to a different Cayley graph and hence to a different condition for G to be δ-hyperbolic, it is known that the notion of hyperbolicity, for some value of δ is actually independent of the generating set. In the language of metric geometry, it is invariant under quasi-isometries
. Therefore, the property of being a hyperbolic group depends only on the group itself.
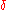 -hyperbolic space. Hyperbolic groups can be characterized as groups G which admit an isometric properly discontinuous action on a proper geodesic Δ-hyperbolic space X such that the factor-space X/G has finite diameter.
-hyperbolic space. Hyperbolic groups can be characterized as groups G which admit an isometric properly discontinuous action on a proper geodesic Δ-hyperbolic space X such that the factor-space X/G has finite diameter.
is surjective in all degrees, or equivalently, in degree 2.
. They are biautomatic and automatic
.: indeed, they are strongly geodesically automatic
, that is, there is an automatic structure on the group, where the language accepted by the word acceptor is the set of all geodesic words.
In a 2010 paper, it was shown that hyperbolic groups have a decidable
marked isomorphism problem. It is notable that this means that the isomorphism problem, orbit problems (in particular the conjugacy problem) and Whitehead's problem are all decidable.
is the notion of a relatively hyperbolic group
. Motivating examples for this generalization are given by the fundamental groups of non-compact hyperbolic manifolds of finite volume, in particular, the fundamental groups of hyperbolic knots, which are not hyperbolic in the sense of Gromov.
A group G is relatively hyperbolic with respect to a subgroup H if, after contracting the Cayley graph of G along H-coset
s, the resulting graph equipped with the usual graph metric is a δ-hyperbolic space and, moreover, it satisfies an additional technical condition which implies that quasi-geodesics with common endpoints travel through approximately the same collection of cosets and enter and exit these cosets in approximately the same place.
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
, a hyperbolic group, also known as a word hyperbolic group, Gromov hyperbolic group, negatively curved group is a finitely generated group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
equipped with a word metric satisfying certain properties characteristic of hyperbolic geometry
Hyperbolic geometry
In mathematics, hyperbolic geometry is a non-Euclidean geometry, meaning that the parallel postulate of Euclidean geometry is replaced...
. The notion of a hyperbolic group was introduced and developed by Mikhail Gromov in the early 1980s. He noticed that many results of Max Dehn
Max Dehn
Max Dehn was a German American mathematician and a student of David Hilbert. He is most famous for his work in geometry, topology and geometric group theory...
concerning the fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
of a hyperbolic Riemann surface
Riemann surface
In mathematics, particularly in complex analysis, a Riemann surface, first studied by and named after Bernhard Riemann, is a one-dimensional complex manifold. Riemann surfaces can be thought of as "deformed versions" of the complex plane: locally near every point they look like patches of the...
do not rely either on it having dimension two or even on being a manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
and hold in much more general context. In a very influential paper from 1987, Gromov proposed a wide-ranging research program. Ideas and foundational material in the theory of hyperbolic groups also stem from the work of George Mostow
George Mostow
George Mostow is an American mathematician, a member of the National Academy of Sciences, Henry Ford II Professor of Mathematics at Yale University, the 49th President of the American Mathematical Society ,...
, William Thurston
William Thurston
William Paul Thurston is an American mathematician. He is a pioneer in the field of low-dimensional topology. In 1982, he was awarded the Fields Medal for his contributions to the study of 3-manifolds...
, James W. Cannon
James W. Cannon
James W. Cannon is an American mathematician working in the areas of low-dimensional topology and geometric group theory. He is an Orson Pratt Professor of Mathematics at Brigham Young University.-Biographical data:...
, Eliyahu Rips
Eliyahu Rips
Eliyahu Rips, also Ilya Rips is a Latvian-born Israeli mathematician known for his research in geometric group theory. He became known to the general public following his coauthoring a paper on the Torah Code....
, and many others.
Definitions
Hyperbolic groups can be defined in several different ways. All definitions use the Cayley graphCayley graph
In mathematics, a Cayley graph, also known as a Cayley colour graph, Cayley diagram, group diagram, or colour group is a graph that encodes the abstract structure of a group. Its definition is suggested by Cayley's theorem and uses a specified, usually finite, set of generators for the group...
of the group and involve a choice of a positive constant δ and first define a δ-hyperbolic group. A group is called hyperbolic if it is δ-hyperbolic for some δ. When translating between different definitions of hyperbolicity, the particular value of δ may change, but the resulting notions of a hyperbolic group turn out to be equivalent.
Let G be a finitely generated group, and T be its Cayley graph
Cayley graph
In mathematics, a Cayley graph, also known as a Cayley colour graph, Cayley diagram, group diagram, or colour group is a graph that encodes the abstract structure of a group. Its definition is suggested by Cayley's theorem and uses a specified, usually finite, set of generators for the group...
with respect to some finite set S of generators. By identifying each edge isometrically with the unit interval in R, the Cayley graph becomes a metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
. The group G acts on T by isometries
Isometry
In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
and this action is simply transitive on the vertices. A path in T of minimal length that connects points x and y is called a geodesic segment and is denoted [x,y]. A geodesic triangle in T consists of three points x, y, z, its vertices, and three geodesic segments [x,y], [y,z], [z,x], its sides.
The first approach to hyperbolicity is based on the slim triangles condition and is generally credited to Rips. Let δ > 0 be fixed. A geodesic triangle is δ-slim if each side is contained in a
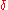 -neighborhood of the other two sides:
-neighborhood of the other two sides:The Cayley graph T is δ-hyperbolic if all geodesic triangles are δ-slim, and in this case G is a δ-hyperbolic group. Although a different choice of a finite generating set will lead to a different Cayley graph and hence to a different condition for G to be δ-hyperbolic, it is known that the notion of hyperbolicity, for some value of δ is actually independent of the generating set. In the language of metric geometry, it is invariant under quasi-isometries
Quasi-isometry
In mathematics, a quasi-isometry is a means to compare the large-scale structure of metric spaces. The concept is especially important in Gromov's geometric group theory.-Definition:...
. Therefore, the property of being a hyperbolic group depends only on the group itself.
Remark
By imposing the slim triangles condition on geodesic metric spaces in general, one arrives at the more general notion of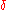 -hyperbolic space. Hyperbolic groups can be characterized as groups G which admit an isometric properly discontinuous action on a proper geodesic Δ-hyperbolic space X such that the factor-space X/G has finite diameter.
-hyperbolic space. Hyperbolic groups can be characterized as groups G which admit an isometric properly discontinuous action on a proper geodesic Δ-hyperbolic space X such that the factor-space X/G has finite diameter.Examples of hyperbolic groups
- Finite groupFinite groupIn mathematics and abstract algebra, a finite group is a group whose underlying set G has finitely many elements. During the twentieth century, mathematicians investigated certain aspects of the theory of finite groups in great depth, especially the local theory of finite groups, and the theory of...
s. - Virtually cyclic groups.
- Finitely generated free groupFree groupIn mathematics, a group G is called free if there is a subset S of G such that any element of G can be written in one and only one way as a product of finitely many elements of S and their inverses...
s, and more generally, groups that actGroup actionIn algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
on a locally finite treeTree (graph theory)In mathematics, more specifically graph theory, a tree is an undirected graph in which any two vertices are connected by exactly one simple path. In other words, any connected graph without cycles is a tree...
with finite stabilizers. - Most surfaceSurfaceIn mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball...
groups are hyperbolic, namely, the fundamental groupFundamental groupIn mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
s of surfaces with negative Euler characteristicEuler characteristicIn mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...
. For example, the fundamental group of the sphere with two handles (the surface of genus two) is a hyperbolic group. - Most triangle groupTriangle groupIn mathematics, a triangle group is a group that can be realized geometrically by sequences of reflections across the sides of a triangle. The triangle can be an ordinary Euclidean triangle, a triangle on the sphere, or a hyperbolic triangle...
s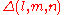 are hyperbolic, namely, those for which 1/l + 1/m + 1/n < 1, such as the (2,3,7) triangle group(2,3,7) triangle groupIn the theory of Riemann surfaces and hyperbolic geometry, the triangle group is particularly important. This importance stems from its connection to Hurwitz surfaces, namely Riemann surfaces of genus g with the largest possible order, 84, of its automorphism group.A note on terminology – the "...
are hyperbolic, namely, those for which 1/l + 1/m + 1/n < 1, such as the (2,3,7) triangle group(2,3,7) triangle groupIn the theory of Riemann surfaces and hyperbolic geometry, the triangle group is particularly important. This importance stems from its connection to Hurwitz surfaces, namely Riemann surfaces of genus g with the largest possible order, 84, of its automorphism group.A note on terminology – the "...
. - The fundamental groups of compact Riemannian manifoldRiemannian manifoldIn Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
s with strictly negative sectional curvatureSectional curvatureIn Riemannian geometry, the sectional curvature is one of the ways to describe the curvature of Riemannian manifolds. The sectional curvature K depends on a two-dimensional plane σp in the tangent space at p...
. - Groups that act cocompactly and properly discontinuously on a proper CAT(k) spaceCAT(k) spaceIn mathematics, a CAT space is a specific type of metric space. Intuitively, triangles in a CAT space are "slimmer" than corresponding "model triangles" in a standard space of constant curvature k. In a CAT space, the curvature is bounded from above by k...
with k < 0. This class of groups includes all the preceding ones as special cases. It also leads to many examples of hyperbolic groups not related to trees or manifolds. - In some sense, "most" finitely presented groups with large defining relations are hyperbolic. See Random groupRandom groupIn mathematics, random groups are certain groups obtained by a probabilistic construction. They were introduced by Misha Gromov to answer questions such as "What does a typical group look like?"...
.
Examples of non-hyperbolic groups
- The free rank 2 abelian groupFree abelian groupIn abstract algebra, a free abelian group is an abelian group that has a "basis" in the sense that every element of the group can be written in one and only one way as a finite linear combination of elements of the basis, with integer coefficients. Hence, free abelian groups over a basis B are...
Z2 is not hyperbolic. - More generally, any group which contains Z2 as a subgroupSubgroupIn group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
is not hyperbolic. In particular, latticesLattice (discrete subgroup)In Lie theory and related areas of mathematics, a lattice in a locally compact topological group is a discrete subgroup with the property that the quotient space has finite invariant measure...
in higher rank semisimple Lie groups and the fundamental groupFundamental groupIn mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
s π1(S3−K) of nontrivial knotKnot (mathematics)In mathematics, a knot is an embedding of a circle in 3-dimensional Euclidean space, R3, considered up to continuous deformations . A crucial difference between the standard mathematical and conventional notions of a knot is that mathematical knots are closed—there are no ends to tie or untie on a...
complements fall into this category and therefore are not hyperbolic. - Baumslag–Solitar groupBaumslag–Solitar groupIn the mathematical field of group theory, the Baumslag–Solitar groups are examples of two-generator one-relator groups that play an important role in combinatorial group theory and geometric group theory as examples and test-cases. They are given by the group presentationFor each integer m and n,...
s B(m,n) and any group that contains a subgroup isomorphic to some B(m,n) fail to be hyperbolic (since B(1,1) = Z2, this generalizes the previous example). - A non-uniform lattice in rank 1 semisimple Lie groups is hyperbolic if and only if the associated symmetric space is the hyperbolic plane.
Homological characterization
In 2002, I. Mineyev showed that hyperbolic groups are exactly those finitely generated groups for which the comparison map between the bounded cohomology and ordinary cohomologyGroup cohomology
In abstract algebra, homological algebra, algebraic topology and algebraic number theory, as well as in applications to group theory proper, group cohomology is a way to study groups using a sequence of functors H n. The study of fixed points of groups acting on modules and quotient modules...
is surjective in all degrees, or equivalently, in degree 2.
Properties
Hyperbolic groups have a solvable word problemWord problem for groups
In mathematics, especially in the area of abstract algebra known as combinatorial group theory, the word problem for a finitely generated group G is the algorithmic problem of deciding whether two words in the generators represent the same element...
. They are biautomatic and automatic
Automatic group
In mathematics, an automatic group is a finitely generated group equipped with several finite-state automata. These automata can tell if a given word representation of a group element is in a "canonical form" and can tell if two elements given in canonical words differ by a generator.More...
.: indeed, they are strongly geodesically automatic
Automatic group
In mathematics, an automatic group is a finitely generated group equipped with several finite-state automata. These automata can tell if a given word representation of a group element is in a "canonical form" and can tell if two elements given in canonical words differ by a generator.More...
, that is, there is an automatic structure on the group, where the language accepted by the word acceptor is the set of all geodesic words.
In a 2010 paper, it was shown that hyperbolic groups have a decidable
Decidable
The word decidable may refer to:* Decidable language*Decidability for the equivalent in mathematical logic*Gödel's incompleteness theorem, a theorem on the indecidability of languages consisting of "true statements" in mathematical logic....
marked isomorphism problem. It is notable that this means that the isomorphism problem, orbit problems (in particular the conjugacy problem) and Whitehead's problem are all decidable.
Generalizations
An important generalization of hyperbolic groups in geometric group theoryGeometric group theory
Geometric group theory is an area in mathematics devoted to the study of finitely generated groups via exploring the connections between algebraic properties of such groups and topological and geometric properties of spaces on which these groups act .Another important...
is the notion of a relatively hyperbolic group
Relatively hyperbolic group
In mathematics, the concept of a relatively hyperbolic group is an important generalization of the geometric group theory concept of a hyperbolic group...
. Motivating examples for this generalization are given by the fundamental groups of non-compact hyperbolic manifolds of finite volume, in particular, the fundamental groups of hyperbolic knots, which are not hyperbolic in the sense of Gromov.
A group G is relatively hyperbolic with respect to a subgroup H if, after contracting the Cayley graph of G along H-coset
Coset
In mathematics, if G is a group, and H is a subgroup of G, and g is an element of G, thenA coset is a left or right coset of some subgroup in G...
s, the resulting graph equipped with the usual graph metric is a δ-hyperbolic space and, moreover, it satisfies an additional technical condition which implies that quasi-geodesics with common endpoints travel through approximately the same collection of cosets and enter and exit these cosets in approximately the same place.
Further reading
- É. Ghys and P. de la Harpe (editors), Sur les groupes hyperboliques d'après Mikhael Gromov. Progress in Mathematics, 83. Birkhäuser Boston, Inc., Boston, MA, 1990. xii+285 pp. ISBN 0-8176-3508-4
- Michel Coornaert, Thomas Delzant and Athanase Papadopoulos, "Géométrie et théorie des groupes : les groupes hyperboliques de Gromov", Lecture Notes in Mathematics, vol. 1441, Springer-Verlag, Berlin, 1990, x+165 pp. MR 92f:57003, ISBN 3-540-52977-2
- Michel Coornaert and Athanase Papadopoulos, Symbolic dynamics and hyperbolic groups. Lecture Notes in Mathematics. 1539. Springer-Verlag, Berlin, 1993, viii+138 pp. ISBN 3-540-56499-3