
Automatic group
Encyclopedia
In mathematics
, an automatic group is a finitely generated group
equipped with several finite-state automata
. These automata can tell if a given word representation of a group element is in a "canonical form" and can tell if two elements given in canonical words differ by a generator.
More precisely, let G be a group and A be a finite set of generators. Then an automatic structure of G with respect to A is a set of finite-state automata:
The property of being automatic does not depend on the set of generators.
The concept of automatic groups generalizes naturally to automatic semigroup
s.
Examples include:
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, an automatic group is a finitely generated group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
equipped with several finite-state automata
Finite state machine
A finite-state machine or finite-state automaton , or simply a state machine, is a mathematical model used to design computer programs and digital logic circuits. It is conceived as an abstract machine that can be in one of a finite number of states...
. These automata can tell if a given word representation of a group element is in a "canonical form" and can tell if two elements given in canonical words differ by a generator.
More precisely, let G be a group and A be a finite set of generators. Then an automatic structure of G with respect to A is a set of finite-state automata:
- the word-acceptor, which accepts for every element of G at least one word in A representing it
- multipliers, one for each
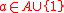 , which accept a pair (w1, w2), for words wi accepted by the word-acceptor, precisely when
, which accept a pair (w1, w2), for words wi accepted by the word-acceptor, precisely when  in G.
in G.
The property of being automatic does not depend on the set of generators.
The concept of automatic groups generalizes naturally to automatic semigroup
Automatic semigroup
In mathematics, an automatic semigroup is a finitely generated semigroup equipped with several regular languages over an alphabet representing a generating set...
s.
Properties
- Automatic groups have word problemWord problem for groupsIn mathematics, especially in the area of abstract algebra known as combinatorial group theory, the word problem for a finitely generated group G is the algorithmic problem of deciding whether two words in the generators represent the same element...
solvable in quadratic time. A given word can actually be put into canonical form in quadratic time.
Examples of automatic groups
- Finite groupFinite groupIn mathematics and abstract algebra, a finite group is a group whose underlying set G has finitely many elements. During the twentieth century, mathematicians investigated certain aspects of the theory of finite groups in great depth, especially the local theory of finite groups, and the theory of...
s, to see this take the regular language to be the set of all words in the finite group. - Negatively curved groups
- Euclidean groupEuclidean groupIn mathematics, the Euclidean group E, sometimes called ISO or similar, is the symmetry group of n-dimensional Euclidean space...
s - All finitely generated Coxeter groupCoxeter groupIn mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example...
s - Braid groupBraid groupIn mathematics, the braid group on n strands, denoted by Bn, is a group which has an intuitive geometrical representation, and in a sense generalizes the symmetric group Sn. Here, n is a natural number; if n > 1, then Bn is an infinite group...
s - Geometrically finite groups
Examples of non-automatic groups
- Baumslag-Solitar groups
- Non-EuclideanEuclidean groupIn mathematics, the Euclidean group E, sometimes called ISO or similar, is the symmetry group of n-dimensional Euclidean space...
nilpotent groupNilpotent groupIn mathematics, more specifically in the field of group theory, a nilpotent group is a group that is "almost abelian". This idea is motivated by the fact that nilpotent groups are solvable, and for finite nilpotent groups, two elements having relatively prime orders must commute...
s
Biautomatic groups
A group is biautomatic if it has two multiplier automata, for left and right multiplication by elements of the generating set respectively. A biautomatic group is clearly automatic.Examples include:
- A hyperbolic groupHyperbolic groupIn group theory, a hyperbolic group, also known as a word hyperbolic group, Gromov hyperbolic group, negatively curved group is a finitely generated group equipped with a word metric satisfying certain properties characteristic of hyperbolic geometry. The notion of a hyperbolic group was introduced...
. - An Artin group of finite type.

